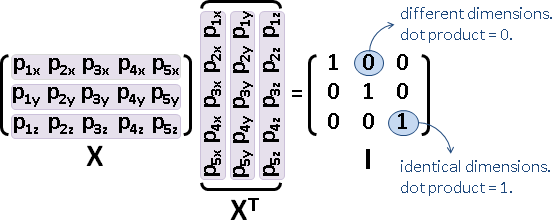
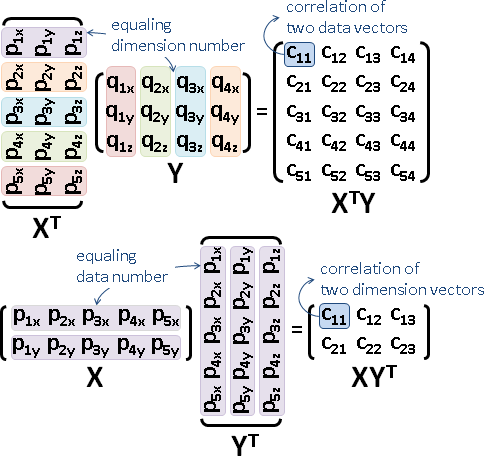
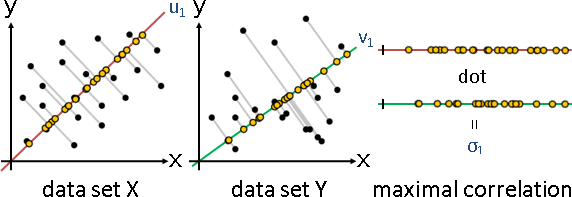
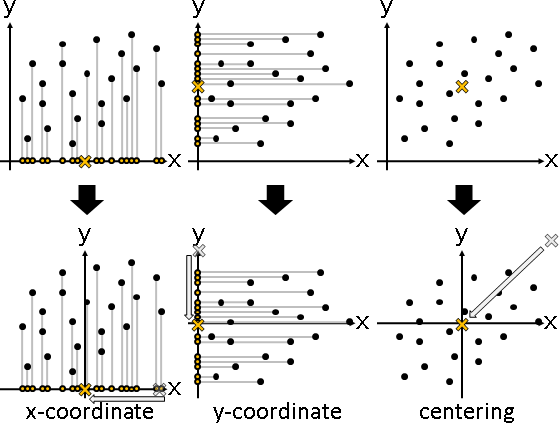
centering

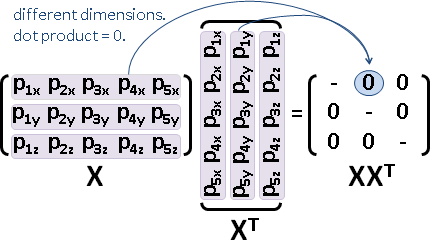
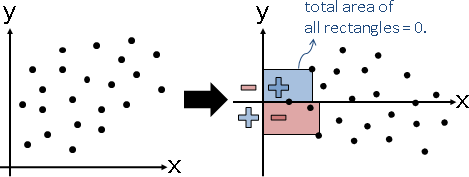
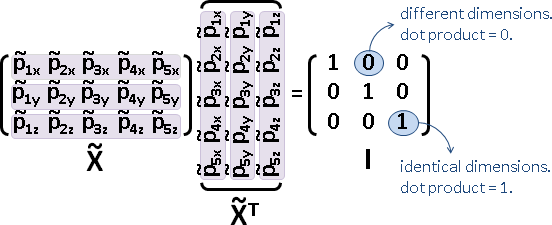
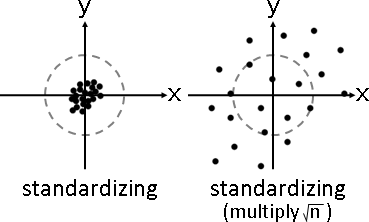
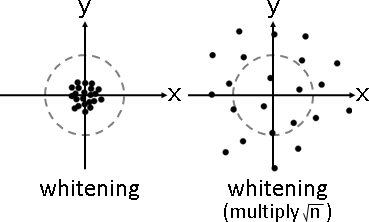
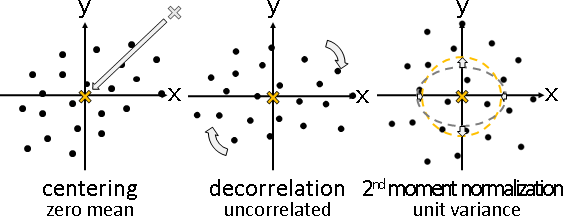
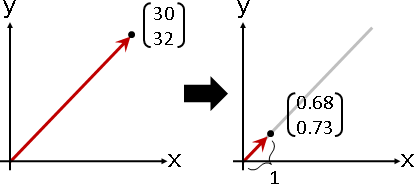
「中心化」。各個維度的總和調成0。數據減去平均數。

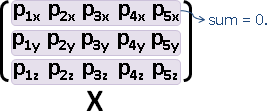
幾何意義：數據中心平移至原點。

const int N = 5; // 數據數量 const int D = 3; // 數據維度 float data[N][D]; // 數據 void centering() { // 行列順序顛倒，經常cache miss。 for (int j=0; j<D; ++j) { float sum = 0; // 總和 for (int i=0; i<N; ++i) sum += data[i][j]; float avg = sum / N; // 平均數 for (int i=0; i<N; ++i) data[i][j] -= avg; } } #include "Eigen/Core" using namespace Eigen; const int D = 3; // 數據維度 const int N = 5; // 數據數量 MatrixXf X(D, N); // 數據矩陣 void centering() { // 三維數據，總共五點。 X << 1, 4, 5, 3, 7, 2, 5, 0, 3, 5, 3, 6, 4, 3, 9; X.colwise() -= X.rowwise().mean(); // 減去平均數 cout << X; }

all-one matrix

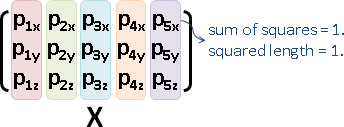
「全一矩陣」。元素全是1。沒有反矩陣。

    ⎡ 1 1 1 ⎤
𝟏 = ⎢ 1 1 1 ⎥
    ⎣ 1 1 1 ⎦

用途：總和、平均數、離差（中心化的結果）。

X = {(1,2,3), (4,5,6), (5,0,4), (3,3,3), (7,5,9)}

data:               one:
                        ⎡ 1 1 1 1 1 ⎤
    ⎡ 1 4 5 3 7 ⎤       ⎢ 1 1 1 1 1 ⎥
X = ⎢ 2 5 0 3 5 ⎥   𝟏 = ⎢ 1 1 1 1 1 ⎥
    ⎣ 3 6 4 3 9 ⎦       ⎢ 1 1 1 1 1 ⎥
                        ⎣ 1 1 1 1 1 ⎦

sum:
       ⎡ 20 20 20 20 20 ⎤
Xsum = ⎢ 15 15 15 15 15 ⎥ = X𝟏
       ⎣ 25 25 25 25 25 ⎦

mean:
    ⎡ 4 4 4 4 4 ⎤
X̄ = ⎢ 3 3 3 3 3 ⎥ = (X𝟏)/n = X(𝟏/n)
    ⎣ 5 5 5 5 5 ⎦

deviation:
    ⎡ 1-4 4-4 5-4 3-4 7-4 ⎤
X̃ = ⎢ 2-3 5-3 0-3 3-3 5-3 ⎥ = X - X(𝟏/n) = X(I - 𝟏/n) = XC
    ⎣ 3-5 6-5 4-5 3-5 9-5 ⎦

centering matrix

「中心化矩陣」。中心化寫成矩陣形式。沒有反矩陣。

              ⎡ 1 0 0 ⎤     ⎡ 1 1 1 ⎤   ⎡  ⅔ -⅓ -⅓ ⎤
C = I - 𝟏/n = ⎢ 0 1 0 ⎥ - ⅓ ⎢ 1 1 1 ⎥ = ⎢ -⅓  ⅔ -⅓ ⎥
              ⎣ 0 0 1 ⎦     ⎣ 1 1 1 ⎦   ⎣ -⅓ -⅓  ⅔ ⎦

中心化矩陣乘在數據矩陣的右邊。

X = {(1,2,3), (4,5,6), (5,0,4), (3,3,3), (7,5,9)}

data:               centering:
                        ⎡  ⅔ -⅓ -⅓ -⅓ -⅓ ⎤
    ⎡ 1 4 5 3 7 ⎤       ⎢ -⅓  ⅔ -⅓ -⅓ -⅓ ⎥
X = ⎢ 2 5 0 3 5 ⎥   C = ⎢ -⅓ -⅓  ⅔ -⅓ -⅓ ⎥
    ⎣ 3 6 4 3 9 ⎦       ⎢ -⅓ -⅓ -⅓  ⅔ -⅓ ⎥
                        ⎣ -⅓ -⅓ -⅓ -⅓  ⅔ ⎦

deviation:
                  ⎡  ⅔ -⅓ -⅓ -⅓ -⅓ ⎤
    ⎡ 1 4 5 3 7 ⎤ ⎢ -⅓  ⅔ -⅓ -⅓ -⅓ ⎥
X̃ = ⎢ 2 5 0 3 5 ⎥ ⎢ -⅓ -⅓  ⅔ -⅓ -⅓ ⎥ = XC
    ⎣ 3 6 4 3 9 ⎦ ⎢ -⅓ -⅓ -⅓  ⅔ -⅓ ⎥
                  ⎣ -⅓ -⅓ -⅓ -⅓  ⅔ ⎦

中心化矩陣可以左乘或右乘，效果不同。

                                          [ 1 4 5 3 7 ]  
                                                +        
⎡ 1 ⎤   ⎡ 4 ⎤   ⎡ 5 ⎤   ⎡ 3 ⎤   ⎡ 7 ⎤     [ 2 5 0 3 5 ]  
⎢ 2 ⎥ + ⎢ 5 ⎥ + ⎢ 0 ⎥ + ⎢ 3 ⎥ + ⎢ 5 ⎥           +        
⎣ 3 ⎦   ⎣ 6 ⎦   ⎣ 4 ⎦   ⎣ 3 ⎦   ⎣ 9 ⎦     [ 3 6 4 3 9 ]  

                X𝟏n×1                         𝟏1×dX

（每個橫條分開調整）直條們總和　　　X𝟏n×n
（每個橫條分開調整）直條們平均　　　X(𝟏n×n/n)
（每個橫條分開調整）各直條減去平均　X - X(𝟏/n) = X(I - 𝟏/n) = XC
（每個直條分開調整）橫條們總和　　　𝟏d×dX
（每個直條分開調整）橫條們平均　　　(𝟏d×d/d)X
（每個直條分開調整）各橫條減去平均　X - (𝟏/d)X = (I - 𝟏/d)X = CX

中心化寫成矩陣運算，繁文縟節。人類深不見底的惡意。

second moment normalization【尚無正式名稱】

「二階動差正規化」。各個維度的平方總和調成1。數據除以平方總和平方根。

矩陣運算觀點：數據矩陣自身外積，對角線調成1。

幾何意義：各個維度的平方總和縮放至1，導致數據長度平方總和縮放至d。

const int N = 5; // 數據數量 const int D = 3; // 數據維度 float data[N][D]; // 數據 void second_moment_normalization() { // 行列順序顛倒，經常cache miss。 for (int j=0; j<D; ++j) { float sum = 0; // 平方總和 for (int i=0; i<N; ++i) sum += data[i][j] * data[i][j]; float avg = sqrt(sum); // 平方總和平方根 for (int i=0; i<N; ++i) data[i][j] /= avg; } } #include "Eigen/Core" using namespace Eigen; const int D = 3; // 數據維度 const int N = 5; // 數據數量 MatrixXf X(D, N); // 數據矩陣 void second_moment_normalization() { // 三維數據，總共五點。 X << 1, 4, 5, 3, 7, 2, 5, 0, 3, 5, 3, 6, 4, 3, 9; X.rowwise().normalize(); // 除以平方總和平方根 cout << X; }

elementwise product（Hadamard product）

「矩陣逐項乘法」、「矩陣點乘」。兩個矩陣對應元素相乘。

    ⎡ 1 4 ⎤       ⎡ 6 3 ⎤         ⎡  6 12 ⎤
A = ⎢ 2 5 ⎥   B = ⎢ 5 2 ⎥   A⊙B = ⎢ 10 10 ⎥
    ⎣ 3 6 ⎦       ⎣ 4 1 ⎦         ⎣ 12  6 ⎦

用途：每項平方、平方總和、平方總和平方根。

data:               squares:
    ⎡ 1 4 5 3 7 ⎤         ⎡ 1 16 25 9 49 ⎤
X = ⎢ 2 5 0 3 5 ⎥   X⊙X = ⎢ 4 25  0 9 25 ⎥
    ⎣ 3 6 4 3 9 ⎦         ⎣ 9 36 16 9 81 ⎦

sum of squares:     square root of sum of squares:
         ⎡ 100 ⎤               ⎡ 10.00 ⎤
(X⊙X)1⃗ = ⎢  63 ⎥    √(X⊙X)1⃗ᵢ = ⎢  7.93 ⎥
         ⎣ 151 ⎦               ⎣ 12.28 ⎦

inverse of square root of sum of squares:
             ⎡ 0.10 ⎤
1/√(X⊙X)1⃗ᵢ = ⎢ 0.12 ⎥
             ⎣ 0.08 ⎦

second moment normalization matrix【尚無正式名稱】

「二階動差正規化矩陣」。縮放矩陣。

    ⎡ 0.10 0    0    ⎤
S = ⎢ 0    0.12 0    ⎥
    ⎣ 0    0    0.08 ⎦

左乘。

     ⎡ 1/0.10 4/0.10 5/0.10 3/0.10 7/0.10 ⎤
SX = ⎢ 2/0.12 5/0.12 0/0.12 3/0.12 5/0.12 ⎥
     ⎣ 3/0.08 6/0.08 4/0.08 3/0.08 9/0.08 ⎦

數據平方總和調成1。自身外積，對角線調成1。

            ⎡ 1    0.83 0.96 ⎤
(SX)(SX)ᵀ = ⎢ 0.83 1    0.92 ⎥
            ⎣ 0.96 0.92 1    ⎦

數學公式：自身點乘、橫向加總、平方根倒數。

S = diag(1/√(X⊙X)1⃗ᵢ) = √((X⊙X)𝟏)⊙I⁻¹

二階動差正規化寫成矩陣運算，繁文縟節。人類太可惡。

standardizing（batch normalization）

「中心化、二階動差正規化」併稱「標準化」。

計算順序影響結果。大家習慣先做中心化、再做二階動差正規化，恰好讓兩者同時成立。

decorrelation

「不相關化」、「去相關」。相異維度的點積調成0。

矩陣運算觀點：數據矩陣自身外積，非對角線調成0。

幾何意義：數據矩形面積總和調成零。一三象限面積為正、二四象限面積為負。也許可以想成是將數據擺正。

conjugate decomposition【尚無正式名稱】

「共軛分解」。A = BᵀB。對稱半正定矩陣分解成矩陣內積。

答案無限多個。常見解法：特徵分解、Cholesky分解。

eigendecomposition:                 Cholesky decomposition:
A = EΛEᵀ= E√Λ√ΛEᵀ = (√ΛEᵀ)ᵀ(√ΛEᵀ)   A = LLᵀ
conjugate decomposition:            conjugate decomposition:
⟌A = √ΛEᵀ                           ⟌A = Lᵀ

decorrelation matrix

「不相關化矩陣」、「去相關矩陣」。有許多種方式，通常是旋轉矩陣。

    ⎡ -0.56 -0.43 -0.71 ⎤
R = ⎢  0.60 -0.80  0.01 ⎥
    ⎣ -0.57 -0.42  0.71 ⎦

左乘。

     ⎡ -3.50  1.59 -1.49 -1.97  5.37 ⎤
RX = ⎢ -1.08 -1.56  2.96 -0.66  0.34 ⎥
     ⎣  0.75 -0.14 -0.01 -0.82  0.23 ⎦

相異維度的點積調成0。自身外積，非對角線調成0。

            ⎡ 299.72   0.00  0.00 ⎤
(RX)(RX)ᵀ = ⎢   0.00  12.96  0.00 ⎥
            ⎣   0.00   0.00  1.32 ⎦

數學公式：自身外積、正規化、共軛分解。

R = ⟌⧚XXᵀ⧛

不相關化寫成矩陣運算，繁文縟節。人類的能力是有極限的。

XXᵀ特徵分解

兩種演算法：X奇異值分解、XXᵀ特徵分解。兩者等價。

(RX)(RX)ᵀ = D     where D is diagonal
RXXᵀRᵀ    = D
REΛEᵀRᵀ   = D     where Λ is diagonal, E is orthogonal
  Λ       = D     let R = E⁻¹ = Eᵀ

相異維度的點積調成0，自身外積調成對角矩陣。

特徵分解XXᵀ = EΛEᵀ。XXᵀ是對稱半正定矩陣，特徵值Λ是非負對角矩陣、特徵向量E是正規正交矩陣。

令R和E相消，剩下對角矩陣，滿足等式。E⁻¹作為不相關化矩陣。

#include "Eigen/Core" #include "Eigen/Dense" using namespace Eigen; void decorrelation() { // 三維數據，總共五點。 MatrixXf X(3, 5); X << 1, 4, 5, 3, 7, 2, 5, 0, 3, 5, 3, 6, 4, 3, 9; MatrixXf C = X * X.transpose(); // 外積矩陣 SelfAdjointEigenSolver<MatrixXf> ed(C); // 特徵分解 MatrixXf E = ed.eigenvectors(); // 特徵向量 MatrixXf R = E.transpose(); // 不相關化矩陣 MatrixXf Y = R * X; // 不相關化 cout << Y; }

X奇異值分解

X = UΣVᵀ             where Σ is diagonal, U and V are orthogonal
U⁻¹X = ΣVᵀ           let R = U⁻¹ = Uᵀ
(ΣVᵀ)(ΣVᵀ)ᵀ = Σ²     where Σ² is diagonal

奇異值分解X_d×n = U_d×dΣ_d×nVᵀ_n×n。奇異值Σ是非負對角矩陣。奇異向量U和V是正規正交矩陣。

ΣVᵀ恰是不相關數據矩陣。ΣVᵀ自身外積恰是對角矩陣。

令U移項。U⁻¹作為不相關化矩陣。

#include "Eigen/Core" #include "Eigen/Dense" using namespace Eigen; void decorrelation() { // 三維數據，總共五點。 MatrixXf X(3, 5); X << 1, 4, 5, 3, 7, 2, 5, 0, 3, 5, 3, 6, 4, 3, 9; JacobiSVD<MatrixXf> svd(X, ComputeFullU);// 奇異值分解 MatrixXf U = svd.matrixU(); // 奇異向量 MatrixXf R = U.transpose(); // 不相關化矩陣 MatrixXf Y = R * X; // 不相關化 cout << Y; }

或者直接將ΣVᵀ當作不相關化結果，自行校正矩陣大小。

void decorrelation() { ...... JacobiSVD<MatrixXf> svd(X, ComputeFullV);// 奇異值分解 MatrixXf V = svd.matrixV().leftCols(3); MatrixXf S = svd.singularValues().asDiagonal(); MatrixXf Y = S * V.transpose(); cout << Y; }

或者採用瘦奇異值分解，自行校正矩陣大小，計算速度更快。

void decorrelation() { ...... JacobiSVD<MatrixXf> svd(X, ComputeThinV);// 瘦奇異值分解 MatrixXf V = svd.matrixV(); MatrixXf S = svd.singularValues().asDiagonal(); MatrixXf Y = S * V.transpose(); Y.conservativeResizeLike(MatrixXf::Zero(3, 5)); cout << Y; }

X奇異值分解＝XXᵀ特徵分解

X = UΣVᵀ
XXᵀ = EΛEᵀ = UΣ²Uᵀ
thus E = U and Λ = Σ²

X奇異值分解，時間複雜度較低。

一般來說，實數對稱半正定矩陣XXᵀ的特徵分解，比普通矩陣X的奇異值分解來得快。可是當X是超大矩陣的情況下，預先計算XXᵀ相當費時，而奇異值分解不必計算XXᵀ，逆轉勝。

去除鏡射

特徵向量不具方向性。特徵向量可以任意對調次序、顛倒方向。

正確答案有許多種。正確答案可以包含鏡射，也可以不包含。

想要去除鏡射，一種想法是窮舉每個向量的方向，從中找到旋轉矩陣。然而時間複雜度太高，沒人這樣做。

另一種想法是讓向量成為右手座標系。

一、標準座標軸（恆等矩陣I）是右手座標系。
二、右手座標系，經過鏡射，得到左手座標系。
　　左手座標系，經過鏡射，得到右手坐標系。
三、右手座標系，經過偶數次鏡射，仍是右手座標系。
　　右手座標系，經過奇數次鏡射，則是左手座標系。
四、偶數次鏡射，得視作一次旋轉。
五、右手座標系經過旋轉，仍是右手座標系。

determinant可以判斷鏡射次數、判斷左手右手座標系。

det(U) = +1，鏡射偶數次，右手座標系。det(U) = -1，鏡射奇數次，左手座標系；再增加一次鏡射，得到右手座標系，例如任取一個向量顛倒方向（元素通通添上負號）。

注意到，左右奇異向量，必須一起顛倒方向。

void decorrelation() { // 三維數據，總共五點。 MatrixXf X(3, 5); X << 1, 4, 5, 3, 7, 2, 5, 0, 3, 5, 3, 6, 4, 3, 9; JacobiSVD<MatrixXf> svd(X, ComputeFullU);// 奇異值分解 MatrixXf U = svd.matrixU(); // 奇異向量 if (U.determinant() < 0) U.col(0) *= -1;// 顛倒方向 MatrixXf R = U.transpose(); // 不相關化矩陣 MatrixXf Y = R * X; // 不相關化 cout << Y; }

whitening

「中心化、二階動差正規化、不相關化」併稱「白化」。

計算順序影響結果。大家習慣依序做中心化、不相關化、二階動差正規化，恰好讓三者同時成立。

白化：計算學的定義方式

大量數據實施白化，將數據搓圓擺正。

中心化：各個維度的總和調成0。Σvᵢ = vᵀ1⃗ = 0, ∀v ∈ rows(X)
不相關化：相異維度的點積調成0。v∙w = vᵀw = 0, ∀v,w ∈ rows(X) and v≠w
二階動差正規化：各個維度的平方總和調成1。‖v‖² = vᵀv = 1, ∀v ∈ rows(X)

矩陣運算觀點：中心化之後，相同維度點積調成1，相異維度點積調成0。中心化結果的自身外積調成恆等矩陣I。

奇異值分解X̃ = UΣVᵀ。Vᵀ自身外積恰是恆等矩陣I。

令UΣ移項。Σ⁻¹Uᵀ作為白化矩陣。Vᵀ作為白化結果。

void whitening() { MatrixXf X(3, 5); X << 1, 4, 5, 3, 7, 2, 5, 0, 3, 5, 3, 6, 4, 3, 9; X.colwise() -= X.rowwise().mean(); // 中心化 JacobiSVD<MatrixXf> svd(X, ComputeThinV); MatrixXf Y = svd.matrixV().transpose(); Y.conservativeResizeLike(MatrixXf::Zero(3, 5)); cout << Y; }

白化：統計學的定義方式

計算學採用離散數值，單位量1，彙集之後形成總和。

統計學採用機率密度函數，機率1/n，彙集之後形成平均。

優點：即便數據數量不同，仍可比較大小。

缺點：計算步驟更多。

　　　　　　　　　計算學　　　　　統計學
中心化　　　　｜總和調成0　　｜平均數調成0　　｜兩者等價
二階動差正規化｜平方總和調成1｜平方平均數調成1｜再乘以√n（或者√n-1）
不相關化　　　｜兩兩點積調成0｜共相關數調成0　｜兩者等價

計算學採用大量數據。

統計學採用分布。分布有三個重要指標、兩個重要性質。

平均數：數據的中心。數據期望值。E[X]
變異數：數據的疏密。數據減去期望值、取平方、期望值。E[(X-E[X])²]
共變異數：數據的正反比。數據減去期望值、相乘、期望值。E[(X-E[X])(Y-E[Y])]

獨立：平行截面均為相同分布。
不相關：相異維度的共相關數是0。（可以改成相關係數、共變異數，意義相同。）

統計學當中，中心化、標準化、白化，以指標與性質來描述。

中心化：調整平均數。
標準化：依序調整平均數、變異數。
　白化：依序調整平均數、共變異數、變異數。

中心化：各個維度的平均數調成0。每筆數據減去平均數。
不相關化：相異維度的共變異數調成0。分布變成不相關。
二階動差正規化：各個維度的變異數調成1。每筆數據除以變異數平方根。

中心化：中心位置平移至原點0。
不相關化：整體數據旋轉至面積平衡。數據擺正。
二階動差正規化：長寬範圍縮放至長度1。

normalization

「正規化」。長度調成一單位。

vector normalization

一個向量的正規化。向量長度調成1。

數學式子：向量除以自身長度（向量除以自身點積平方根）。

 v      v        v
——— = —————— = —————
‖v‖   √‖v‖²    √v∙v

void vector_normalization() { MatrixXf v(3, 1); v << 1, 2, 3; v.normalize(); cout << v; }

data normalization

大量數據的正規化。每筆數據視作向量，各自正規化。

正規化調整直條，二階動差正規化調整橫條。長度調成1。

void normalization() { MatrixXf X(3, 5); X << 1, 4, 5, 3, 7, 2, 5, 0, 3, 5, 3, 6, 4, 3, 9; X.colwise().normalize(); cout << X; }

matrix normalization【尚無正式名稱】

一個矩陣的正規化。瘦矩陣是自身內積調成I，胖矩陣是自身外積調成I，方陣是兩者皆調成I。

數學式子：矩陣除以自身長度（矩陣除以自身內積平方根）。

thin matrix:
       A      A
⧚A⧛ = ——— = ————— = A√AᵀA⁻¹ = UΣVᵀVΣ⁻¹Vᵀ = UVᵀ
      ‖A‖   √AᵀA

fat matrix:
⧚A⧛ = √AAᵀ⁻¹A = UΣ⁻¹UᵀUΣVᵀ = UVᵀ

void matrix_normalization() { MatrixXf A(3, 5); A << 1, 4, 5, 3, 7, 2, 5, 0, 3, 5, 3, 6, 4, 3, 9; MatrixXf ‖A‖² = A.transpose() * A; // 自身內積 MatrixXf ‖A‖⁻¹ = C.sqrt().inverse(); // 平方根倒數 MatrixXf ⧚A⧛ = A * ‖A‖⁻¹; // 正規化 cout << ⧚A⧛; /* 矩陣平方根倒數，目前沒有高速演算法。等你幫忙翻身！ */ } void matrix_normalization() { MatrixXf A(3, 5); A << 1, 4, 5, 3, 7, 2, 5, 0, 3, 5, 3, 6, 4, 3, 9; JacobiSVD<MatrixXf> svd(A, ComputeThinU | ComputeThinV); MatrixXf ⧚A⧛ = svd.matrixU() * svd.matrixV().transpose(); cout << ⧚A⧛; }

data whitening

大量數據的白化。先中心化、再矩陣正規化。

數據矩陣通常是胖矩陣。胖矩陣正規化＝二階動差正規化＋不相關化＋乘以正規正交矩陣。

白化數據，再乘以正規正交矩陣，仍是白化數據。

⧚X̃⧛ = √X̃X̃ᵀ⁻¹X̃ = UΣ⁻¹UᵀX̃

 X̃        = UΣVᵀ
 X̃X̃ᵀ      = UΣ²Uᵀ
√X̃X̃ᵀ      = UΣUᵀ
√X̃X̃ᵀ⁻¹    = UΣ⁻¹Uᵀ
√X̃X̃ᵀ⁻¹X̃   = UΣ⁻¹UᵀX̃

                  centering:      X ->       X̃  }
              decorrelation:      X̃ ->     UᵀX̃  } whitening
second moment normalization:    UᵀX̃ ->  Σ⁻¹UᵀX̃  }
        rotation/reflection: Σ⁻¹UᵀX̃ -> UΣ⁻¹UᵀX̃

「共變異矩陣的平方根倒數」可以作為「白化矩陣」。

W = √X̃X̃ᵀ⁻¹ = UΣ⁻¹Uᵀ

covariance matrix:  X̃X̃ᵀ
      square root: √X̃X̃ᵀ
          inverse: √X̃X̃ᵀ⁻¹

void whitening() { MatrixXf X(3, 5); X << 1, 4, 5, 3, 7, 2, 5, 0, 3, 5, 3, 6, 4, 3, 9; X.colwise() -= X.rowwise().mean(); // 中心化 MatrixXf C = X * X.transpose(); // 共變異矩陣 MatrixXf W = C.sqrt().inverse(); // 平方根倒數 MatrixXf Y = W * X; // 白化 cout << Y; } void whitening() { MatrixXf X(3, 5); X << 1, 4, 5, 3, 7, 2, 5, 0, 3, 5, 3, 6, 4, 3, 9; X.colwise() -= X.rowwise().mean(); // 中心化 JacobiSVD<MatrixXf> svd(X, ComputeThinU | ComputeThinV); MatrixXf Y = svd.matrixU() * svd.matrixV().transpose(); Y.conservativeResizeLike(MatrixXf::Zero(3, 5)); cout << Y; }

延伸閱讀：數學符號

由於尚無正式名稱，我只好自己瞎掰數學符號了。

X̄ = X(𝟏/n)               mean
X̃ = X - X̄ = X(I - 𝟏/n)   deviation (centering)
‖X‖ = √XᵀX               length
⧚X⧛ = X / ‖X‖ = X‖X‖⁻¹   unit (normalization)

correlation

「相關」。兩物的巧合程度。

vector correlation

兩物相乘，稱作「共相關數correlation」。

兩個數字的共相關數：兩數相乘ab。
兩個向量的共相關數：兩向量點積x∙y。
兩個浮動數字的共相關數：兩數相乘期望值E[XY]。

事先正規化，稱作「餘弦相似度cosine similarity」。

兩個數字的餘弦相似度：cos(a,b) = (a/|a|)(b/|b|) = (ab)/(|a||b|)
兩個向量的餘弦相似度：cos(x,y) = (x/‖x‖)∙(y/‖y‖) = (x∙y)/(‖x‖‖y‖)
兩個浮動數字的餘弦相似度：cos(X,Y) = E[XY] / (√E[XX] √E[YY])

事先中心化，稱作「共變異數covariance」。

兩個數字的共變異數：0
兩個向量的共變異數：0
兩個浮動數字的共變異數：cov(X,Y) = E[X̃Ỹ] = E[(X-E[X])(Y-E[Y])]

事先標準化，稱作「相關係數correlation coefficient」。

兩個數字的相關係數：0
兩個向量的相關係數：0
兩個浮動數字的相關係數：corr(X,Y) = E[X̃Ỹ] / (√E[X̃X̃] √E[ỸỸ])

事先白化，沒有名稱。

vector pairwise correlations

兩物相乘，衍生兩種版本。大家習慣採用維度版本。

數據版本：數據兩兩點積是矩陣內積XᵀY。維度數量必須一樣多。
維度版本：維度兩兩點積是矩陣外積XYᵀ。數據數量必須一樣多。

兩兩相乘，稱作「共相關矩陣correlation matrix」。

兩堆數據的共相關矩陣：Rxʏ = XYᵀ
兩堆浮動數字的共相關矩陣：Rxʏ(i,j) = E[XᵢYⱼ]

事先中心化，稱作「共變異數矩陣covariance matrix」。

兩堆數據的共變異數矩陣：Cxʏ = (X-X̄)(Y-Ȳ)ᵀ = X̃Ỹᵀ
兩堆浮動數字的共變異數矩陣：Cxʏ(i,j) = cov(Xᵢ,Yⱼ) = E[X̃ᵢỸⱼ]

事先標準化，稱作「相關係數矩陣correlation coefficient matrix」。因為經常使用，所以大家經常直接稱作「相關矩陣」。

兩堆數據的相關係數矩陣：Pxʏ = (SX̃)(SỸ)ᵀ
兩堆浮動數字的相關係數矩陣：Pxʏ(i,j) = corr(Xᵢ,Yⱼ) = E[X̃ᵢỸⱼ] / (√E[X̃ᵢX̃ᵢ] √E[ỸⱼỸⱼ])

事先白化，沒有名稱。

data correlation

兩堆數據的共相關數。共相關矩陣的奇異值分解XYᵀ = UΣVᵀ，最大的奇異值σ₁，作為共相關數。

幾何意義：找到向量u和v。X投影到向量u，Y投影到向量v，投影量各視作一個向量，讓兩向量共相關數最大。

u和v恰是最大的奇異值的左右奇異向量u₁和v₁，投影量共相關數恰是奇異值σ₁。

最大可以推廣成前幾大，直線可以推廣成平面、空間、……。

XYᵀ = UΣVᵀ
UᵀXYᵀV = Σ          (U⁻¹ = Uᵀ, V⁻¹ = Vᵀ)
(UᵀX)(VᵀY)ᵀ = Σ
(uᵢᵀX)(vᵢᵀY)ᵀ = σᵢ
dot((uᵢᵀX)ᵀ, (vᵢᵀY)ᵀ) = σᵢ
dot(proj_uᵢ(X), proj_vᵢ(Y)) = σᵢ

順帶一提，古人在探索過程當中，發明許多冗餘名詞。

《Characterizing the Response of PET and fMRI Data using Multivariate Linear Models》

partial least squares regression  X與Y都預先中心化
orthonormalized PLS regression    X預先白化、Y預先中心化
canonical correlation analysis    X與Y都預先白化

const int DX = 5; // 數據維度 const int DY = 7; // 數據維度 const int N = 3; // 數據數量 MatrixXf X(DX, N); MatrixXf Y(DY, N); // NIPALS void correlation() { MatrixXf u(X.rows(), 1); MatrixXf v(Y.rows(), 1); MatrixXf v0(Y.rows(), 1); float max = -1e9, pos = 0; for (int j=0; j<Y.cols(); ++j) { float length2 = Y.col(j).squaredNorm(); if (length2 > max) {max = length2; pos = j;} } v = Y.col(pos).normalized(); do { v0 = v; u = (X * (Y.transpose() * v)).normalized(); v = (Y * (X.transpose() * u)).normalized(); } while ((v - v0).squaredNorm() > 1e-15); float s = (X * (Y.transpose() * v)).norm(); cout << s; }