signal
signal（time series）
「訊號」就是一串數字。
數學家稱作數列（離散）、函數（連續）。
訊號學家稱作數位訊號（離散）、類比訊號（連續）。
常見的signal
合成波：正弦波、方波、三角波、脈衝波。
脈衝函數：Dirac函數、高斯函數、sinc函數。
成長速率：步進函數、sigmoid函數、logistic函數。
市場波動：Gaussian process、Wiener process。
雜訊：AGWN。
signal的性質
脈衝：忽然劇烈變化、迅速還原。
週期：特定片段重複無限多次。通常稱作波。
穩態：最終收斂於特定常數。
signal的指標
平均數、變異數、偏度、峰度、ANOVA、能量、訊噪比、頻率、週期、過零率、……。
知名工具tsfresh。
signal quantization
signal sampling
訊號取樣。時間軸離散化。保留重點，刪除細節。
signal quantization
訊號量化。數值軸離散化。保留重點，刪除細節。
簡易的量化是四捨五入、無條件捨去、無條件進入。進階的量化是區分數量級。經典的量化是以圖表相較並沒有明顯差異。
演算法（vector quantization）（cluster analysis）
先分群，以群集中心作為量化結果。
再分類，以分界線決定量化結果。
演算法（location-allocation analysis）
加強版。直線距離改成了其他指標。
演算法（product quantization）
分段、各自量化、合併。
signal resampling
signal reconstruction
訊號重建。找到原本曲線。找到內插函數。
一、訊號通常很長。如果採用多項式內插，那麼內插函數必須是非常高次的多項式，才能穿過所有訊號。然而，非常高次的多項式，劇烈震盪，無法平順的穿過訊號，稱作「Runge's phenomenon」。
二、訊號通常取自真實世界、源自物理現象。例如聲音訊號，是由不同頻率的波，疊加而成的。詳見「傅立葉轉換」。
由於上述兩點，因而衍生了其他內插演算法。
signal resampling
訊號重新取樣。改變疏密程度，重新設計訊號。
變密稱作upsampling、變疏稱作downsampling。也有人把變密稱作interpolation、變疏稱作decimation。
訊號重新取樣＝訊號重建＋函數求值。
演算法（triangle interpolation）（linear interpolation）
三角波。等價於一次內插。不切實際，但是算得快。
演算法（sinc interpolation）
sinc函數。用於已經過濾頻率區段的訊號。
矩形函數，實施逆向傅立葉轉換，頻域轉時域（反過來也行），就是sinc函數。如果頻域只有特定幾個頻率擁有強度（理論上是無限薄的脈衝函數，實際上是有點厚的矩形函數），那麼時域就是特定幾個時間出現sinc函數。算得極慢。
演算法（Lanczos interpolation）
加強版。自由調整胖瘦。砍掉綿延的小波，只留主要的部分。
演算法（Mitchell–Netravali filter）
加強版。改用三次多項式函數模擬之。算得快。
演算法（spline interpolation）
兩個相鄰函數點，取左右鄰近函數點們做內插，只取兩個相鄰函數點之間那一段函數曲線。所有相鄰函數點，如法炮製。每一段函數曲線，一段一段接起來。
藉由左右鄰近函數點數，可以控制平滑程度。主要用於微分方程式之數值模擬。
signal prediction🚧
signal estimation（time series fitting）
訊號估計。找到理想曲線。找到規律。找到迴歸函數。
迴歸函數是遞迴函數、週期函數等等具有規律的函數。
signal prediction（time series forecasting）
訊號預測。訊號有某種規律，請預測接下來的訊號。
訊號預測＝訊號估計＋函數求值。
演算法（linear prediction）（linear predictive coding）
請見本站文件「filter」。
linear regression：用一次函數符合資料。linear prediction：用線性遞迴函數符合資料。
誤差設定成「均方誤差mean squared error」：平方誤差，再除以數列長度；平方誤差的平均數。如此一來，長度不同的數列，得以互相比較誤差大小。
首先求得均方誤差最小的線性遞迴函數。時間複雜度O(N²)，在頻域計算可加速為O(NlogN)。
求得線性遞迴函數之後，欲預測下一個新訊號，直接代入最後K個舊訊號即可。時間複雜度O(K)，K是線性遞迴函數的項數。
求得線性遞迴函數之後，欲預測第M個新訊號，共有四種演算法。時間複雜度O(K²logM)，在頻域計算可加速為O(KlogKlogM)。
演算法（ARIMA）
加強版。遞迴關係式增加項次。
演算法（ARCH）
加強版。推廣成非線性，引入統計學。
演算法（Prophet）
演算法（Kalman filter）（linear quadratic estimation）
觀察值與預測值的一次內插。
推定預測值源自線性遞迴公式。
演算法（recurrent neural network）
signal smoothing🚧
signal denoising
訊號降噪。降低雜訊大小。
signal denoising = signal estimation。一體兩面。
例如大家習慣使用Kalman filter抑制運動軌跡雜訊。位置、速度、加速度，有限差分，強行展開，即是線性遞迴公式。經典範例是登月大空梭，藉由Kalman filter讓太空梭從地球飛到月球。
signal smoothing
訊號平滑化。降低鄰近數字差異大小。
signal smoothing可以抑制雜訊。如果雜訊的平均數是零，那麼平滑化可以完全消除雜訊，代價是訊號本身也變成平均數了。
維基百科整理了一份演算法名稱列表：
演算法（moving average）
移動平均。鄰近函數點的加權平均數，作為該函數點。
演算法（local regression）（moving regression）
局部迴歸。鄰近函數點進行迴歸。根據迴歸函數，重新計算該函數點。
另外，當迴歸函數是連續函數，則可以計算該函數點的任意次微分。
演算法（Savitzky–Golay filter）
Why and How Savitzky–Golay Filters Should Be Replaced https://pubs.acs.org/doi/10.1021/acsmeasuresciau.1c00054
演算法（LOESS: locally estimated scatterplot smoothing）
處理outlier。原版即是Savitzky–Golay filter。
做兩次。第一次用k-nearest neighbor，第二次用移動平均。
https://www.mathworks.com/help/curvefit/smooth.html https://www.ime.unicamp.br/~dias/loess.pdf https://en.wikipedia.org/wiki/Local_regression
演算法（exponential smoothing）
觀察值與預測值的一次內插。
強行展開，各項係數呈指數成長，因而得名。
強行展開可以視作移動平均，但是每回合權重都不一樣。
exponential smoothing yn = (1-a) yn-1 + a xn double exponential smoothing triple exponential smoothing
signal separation🚧
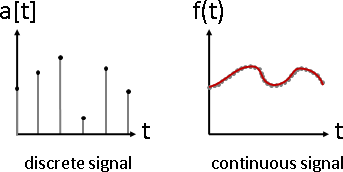
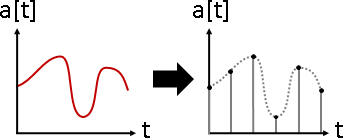
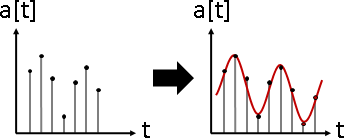
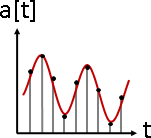
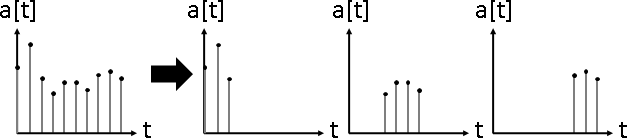
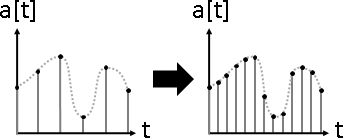signal overlapping（signal composition）
訊號疊加。數據軸加法。大量訊號疊合在一起。
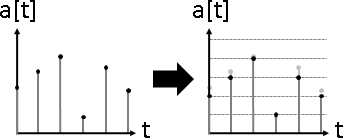
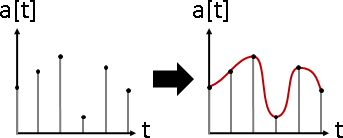
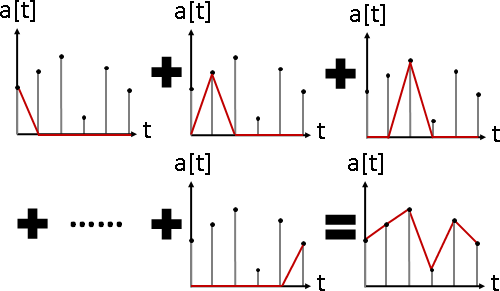
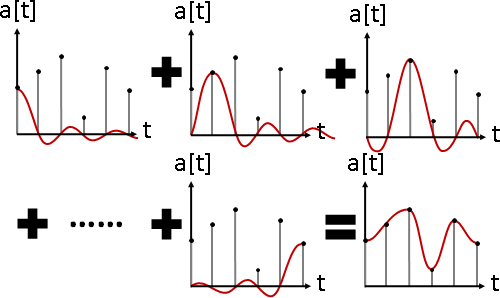
signal separation（signal decomposition）
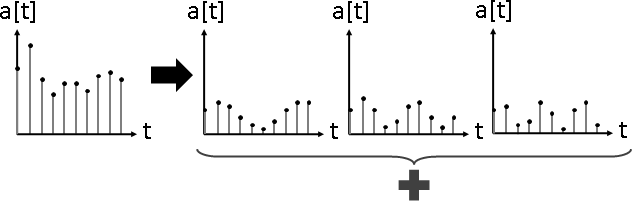
訊號分隔。數據軸分割。大量訊號疊合在一起，分隔每道訊號。
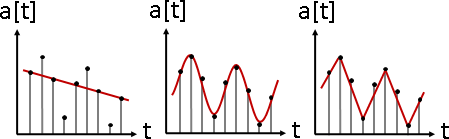
trend中線, seasional週期, cyclic峰谷, noise雜訊 yₙ = tₙ + sₙ + cₙ + nₙ
https://www.abs.gov.au/websitedbs/d3310114.nsf/4a256353001af3ed4b2562bb00121564/5fc845406def2c3dca256ce100188f8e https://cran.r-project.org/web/packages/deseats/readme/README.html
演算法（Henderson moving average）
Spencer https://robjhyndman.com/papers/movingaverage.pdf https://mathworld.wolfram.com/Spencers15-PointMovingAverage.html
演算法（Whittaker–Henderson filter）
regularization，追加平滑程度。
min { sum wₙ (yₙ - tₙ)² + λ sum (dⁿ/dxⁿ tₙ)² }
t n n
演算法（Hodrick–Prescott filter）
平滑程度改成二階差分。擁有公式解。
N N-1
min { sum (yₙ - tₙ)² + λ sum ((tₙ₊₁ - tₙ) - (tₙ - tₙ₋₁))² }
t n=1 n=2
公式解矩陣
https://en.wikipedia.org/wiki/Hodrick–Prescott_filter https://en.wikipedia.org/wiki/Smoothing_spline Why you should never use the Hodrick–Prescott filter https://www.nber.org/system/files/working_papers/w23429/w23429.pdf An Exploration of Trend-Cycle Decomposition Methodologies in Simulated Data https://papers.ssrn.com/abstract=3539317
演算法（smoothing spline）
迴歸函數換成spline。
N N-1
min { sum (yₙ - fₙ)² + λ sum (d²/dx² fₙ)² }
f n=1 n=2
where f is spline
signal segmentation🚧
signal concatenation
訊號銜接。時間軸銜接。大量訊號銜接在一起。
主要問題在於曲線不連續。在於相位。淡入淡出也無法解決。
signal segmentation
訊號分段。時間軸分割。大量訊號銜接在一起，分割每段訊號。
signal representation🚧
signal transformation
訊號變換。訊號套用函數，改變訊號造型。
signal representation
訊號表示。訊號套用函數，換個視角呈現訊號。
演算法（Karhunen–Loève transform）（Hotelling transform）
即是principal component analysis。
演算法（sparse coding）
signal classification🚧
signal detection
訊號偵測。判斷訊號是資訊或是雜訊。
signal classification
訊號分類。判斷訊號是哪種常見訊號。
演算法（hidden Markov model）
演算法（catch22: canonical time-series characteristic）
https://www.sktime.net/en/v0.20.0/examples/02_classification.html
signal recovery🚧
signal completion
訊號補全。訊號部分佚失，推敲原本訊號。
signal recovery
訊號還原。訊號部分錯誤，推敲原本訊號。