Markov model

馬可夫模型大意是：選一個狀態作為起點，然後沿著邊隨意走訪任何一個狀態，一直走一直走，沿途累計機率，走累了就停在某個狀態。

熟悉「圖論」的讀者應該很快就能上手，馬可夫模型的外觀看起來就是圖──只不過代數符號多得令人生厭。

建議閱讀：L. Rabiner, A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition, Proceedings of the IEEE, vol. 77, No. 2, February 1989.

state, S

圖片中，每一個圓圈叫做一個「狀態」。馬可夫模型一共有N個狀態，通常標作s₁到s_N。N是我們自行設定的常數。

全部狀態構成的集合，標作大寫S。

transition probability, A

每一個狀態都會射出N條邊，這N條邊分別連向每一個狀態，這N條邊的數值都是機率，這N條邊的數值皆介於0到1，這N條邊的數值總和必為1，滿足機率公設。

一條由狀態sᵢ到狀態sⱼ的邊，其數值通常標作aᵢⱼ。亦可標作條件機率P( sⱼ | sᵢ )，意思是現在在狀態sᵢ、要來去狀態sⱼ。亦可套用稍後提到的狀態序列，標作P( q_t+1 = j | qₜ = i )。

全部邊構成的集合，標作A。通常把A看作一個N×N矩陣。

寫程式時，我們可以利用圖的資料結構adjacency matrix儲存全部的數值。當A有很多數值是零，去掉一些邊之後，也可以改用adjacency lists。

initial probability, Π

我們可以選擇任何一個狀態作為起點。機率總和為1。

繪製圖片時，我們可以設計一個虛幻狀態s₀，讓s₀射出N條虛幻邊，分別連向每一個狀態，其數值滿足機率公設。如此一來我們就可以從冥冥之中的s₀開始行動。

這N條虛幻邊的數值通常標作π₁到π_N。亦可標作機率P( s₁ )到P( s_N )。亦可套用稍後提到的狀態序列，標作P( q₁ = 1 )到P( q₁ = N )。

這N條虛幻邊構成的集合，標作Π。通常把Π看作一個N維向量、一個N×1矩陣。

寫程式時，通常我們不會設計一個虛幻的狀態s₀，而是把狀態s₁到s_N重新標作s₀到s_N-1。

const int N = 3; double a[N][N]; double π[N];

state sequence, q₁ q₂ ...... q_T

選定起點後，可以沿著邊，到處走來走去，一路走過T個狀態以及T-1條邊之後，就停下來。T是我們自行設定的常數。

一條路徑，通常標作q₁ q₂ ...... q_T，為途經的狀態編號。

一條路徑的機率，可以寫成π_q₁ × a_q₁q₂ × ...... × a_qT-1qT，也可以寫成P( s_q₁ ) × P( s_q₂ | s_q₁ ) × ...... × P( s_qT | s_qT-1 )。

const int N = 3; double π[N], a[N][N]; // Markov model double probability(int* q, int T) { double p = π[q[0]]; for (int i=1; i<T; ++i) p *= a[q[i-1]][q[i]]; return p; }

延伸閱讀：time variant

馬可夫模型的A的數值，會隨時間而改變。

時刻t，一條由狀態sᵢ到狀態sⱼ的邊，其數值通常標作a_tᵢⱼ。

平常不會搞到這麼複雜啦。一般只用time invariant。

延伸閱讀：order

馬可夫模型的A的數值，會受到來源狀態影響。

如果只受到上一個狀態影響，稱作first-order，也就是我們慣用的：一條由狀態sᵢ到狀態sⱼ的邊，其數值標作aᵢⱼ，亦可標作P( sⱼ | sᵢ )，亦可標作P( q_t+1 = j | qₜ = i )。

如果受到上一個狀態、上上個狀態影響，稱作second-order：其數值標作aᵢⱼₖ，亦可標作P( sₖ | sᵢⱼ )，亦可標作P( q_t+1 = k | qₜ = j , q_t-1 = i )。

如果受到以前所有狀態影響，我不知道要稱作甚麼：可標示成條件機率P( q_t+1 = j | qₜ = iₜ , q_t-1 = i_t-1 , ...... , q₀ = i₀ )。

平常不會搞到這麼複雜啦。一般只用first-order。

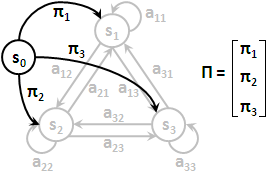
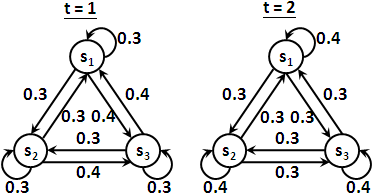
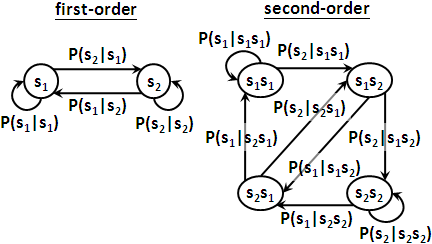
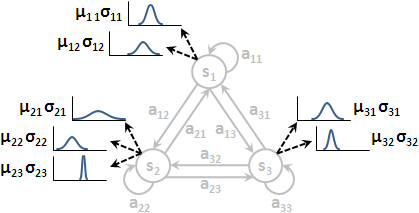
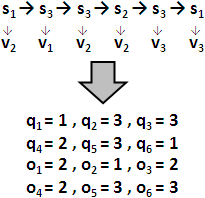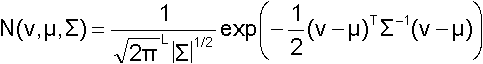observation, V

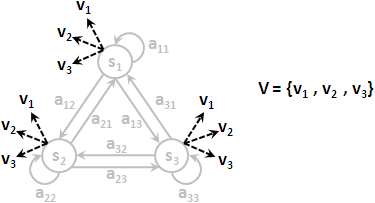
隱藏馬可夫模型添加了一個新要素：每當造訪一個狀態，就立刻從M個值當中，噴出其中一個值。每一個狀態都是噴出相同的M種值，這M個值通常標作v₁到v_M。M是我們自行設定的常數。

全部觀察構成的集合，標作大寫V。

observation probability, B

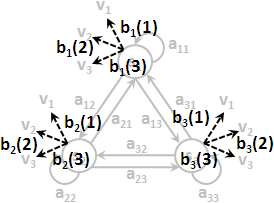
每一個狀態噴出這M種值的機率都不相同。

狀態sᵢ噴出vₖ的機率，通常標作bᵢ( k )或者簡單標作bᵢₖ。亦可標作條件機率P( vₖ | sᵢ )，意思是現在在狀態sᵢ、噴出觀察vₖ。亦可套用狀態序列與觀察序列，標作P( oₜ = k | qₜ = i )。

每個狀態各自的噴出機率構成的集合，標作B。通常把B看作N個函數，或者簡單地看作一個N×M矩陣。

observation sequence, o₁ o₂ ...... o_T

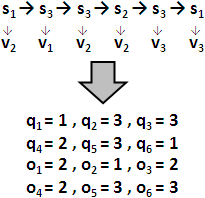
走T步後，一路上T個狀態個別噴出的值的編號。

有了狀態序列與觀察序列，一條路徑的機率，可以寫成π_q₁ × b_q₁( o₁ ) × a_q₁q₂ × b_q₂( o₂ ) × ...... × a_qT-1qT × b_qT( o_T )，也可以寫成P( s_q₁ ) × P( v_o₁ | s_q₁ ) × P( s_q₂ | s_q₁ ) × P( v_o₂ | s_q₂ ) × ...... × P( s_qT | s_qT-1 ) × P( v_oT | s_qT )。我想各位差不多眼花撩亂了。名可名也，非恒名也，若能領會原理就不用刻意背誦代數了。

const int N = 3, M = 3, T = 15; double π[N], a[N][N], b[N][M]; // HMM double probability(int* q, int* o, int T) { double p = π[q[0]] * b[q[0]][o[0]]; for (int i=1; i<T; ++i) p *= a[q[i-1]][q[i]] * b[q[i]][o[i]]; return p; }

hidden Markov model

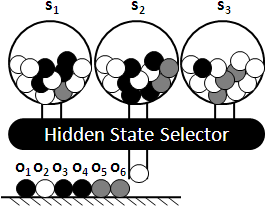
隱藏馬可夫模型的特色就是：我們只看到了觀察序列（果），但是我們看不到狀態序列（因）；我們只看到了依序噴出的T個值，但是我們看不到一路走過的是哪T個狀態。

「隱藏」二字便是指行蹤被隱藏了，狀態序列被隱藏了。

接下來要討論隱藏馬可夫模型的三個基本問題，以及演算法。

1. evaluation problem: forward-backward algorithm

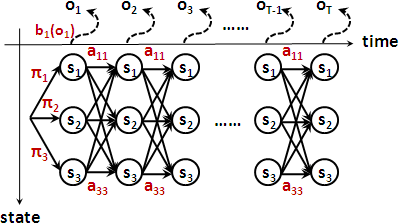
看到一個觀察序列o₁ o₂ ...... o_T，但是看不到狀態序列s₁ s₂ ...... s_T的情況下，找出所有可能的路徑的機率的總和。

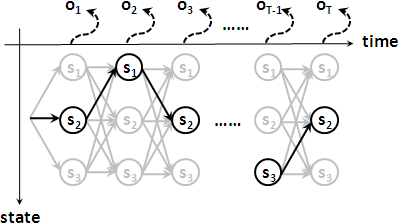
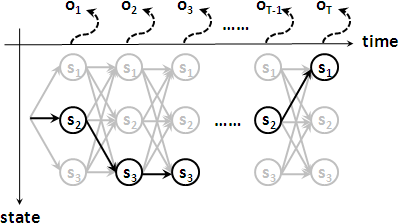
對於一個觀察序列來說，狀態序列有各式各樣的可能性，一共有Nᵀ種可能性。

運用窮舉法，時間複雜度O(NᵀT)。運用「動態規劃」，時間複雜度降低為O(N²T)。

原理是結合律，比如x×b×c + y×b×c + z×b×c = (x+y+z)×b×c，能加的先加一加。左端結合是forward，右端結合是backward；使用其中一種即可，計算結果都一樣。

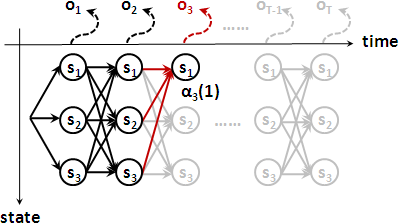
forward:
α₁(j) = πⱼ × bⱼ(o₁)
αt+1(j) = ∑i=1⋯N[ αₜ(i) × aᵢⱼ ] × bⱼ(ot+1)

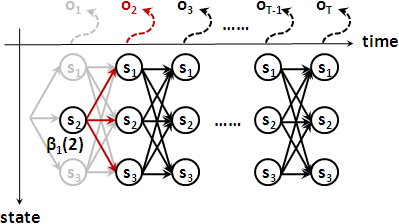
backward:
βT(i) = 1
βₜ(i) = ∑j=1⋯N[ aᵢⱼ × bⱼ(ot+1) × βt+1(j) ]

const int N = 3, M = 3, T = 15; double π[N], a[N][N], b[N][M]; // HMM double α[T][N]; // 可以簡化成α[2][N] double β[T][N]; // 可以簡化成β[2][N] double forward(int* o, int T) { for (int t=0; t<T; ++t) for (int j=0; j<N; ++j) if (t == 0) α[t][j] = π[j] * b[j][o[t]]; else { double p = 0; for (int i=0; i<N; ++i) p += α[t-1][i] * a[i][j]; α[t][j] = p * b[j][o[t]]; } double p = 0; for (int i=0; i<N; ++i) p += α[T-1][i]; return p; } double backward(int* o, int T) { for (int t=T-1; t>=0; --t) for (int i=0; i<N; ++i) if (t == T-1) β[t][i] = 1.0; else { double p = 0; for (int j=0; j<N; ++j) p += a[i][j] * b[j][o[t+1]] * β[t+1][j]; β[t][i] = p; } double p = 0; for (int j=0; j<N; ++j) p += π[j] * b[j][o[0]] * β[0][j]; return p; }

2. decoding problem: Viterbi algorithm

看到一個觀察序列o₁ o₂ ...... o_T，但是看不到狀態序列s₁ s₂ ...... s_T的情況下，從所有可能的路徑當中，找出機率最大的一條路徑，以及其機率。

這跟上一個問題如出一轍，運用「動態規劃」就可以解決。唯一的差別就是把∑換成max而已。

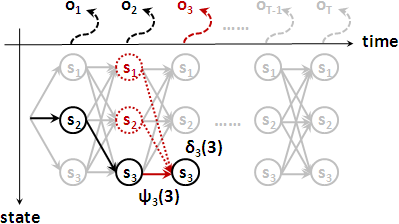
forward:
δ₁(j) = πⱼ × bⱼ(o₁)
δt+1(j) = maxi=1⋯N[ δₜ(i) × aᵢⱼ ] × bⱼ(ot+1)

path tracing:
ψₜ(j) = arg maxi=1⋯N[ δt-1(i) × aᵢⱼ ] × bⱼ(oₜ)
      = arg maxi=1⋯N[ δt-1(i) × aᵢⱼ ]

const int N = 3, M = 3, T = 15; double π[N], a[N][N], b[N][M]; // HMM double δ[T][N]; // 可以簡化成δ[2][N] int ψ[T][N]; double decode(int* o, int T, int* q) { for (int t=0; t<T; ++t) for (int j=0; j<N; ++j) if (t == 0) δ[t][j] = π[j] * b[j][o[t]]; else { double p = -1e9; for (int i=0; i<N; ++i) { double w = δ[t-1][i] * a[i][j]; if (w > p) p = w, ψ[t][j] = i; } δ[t][j] = p * b[j][o[t]]; } double p = -1e9; for (int j=0; j<N; ++j) if (δ[T-1][j] > p) p = δ[T-1][j], q[T-1] = j; for (int t=T-1; t>0; --t) q[t-1] = ψ[t][q[t]]; return p; }

3. training problem: EM algorithm

給定一個觀察序列o₁ o₂ ...... o_T，更新ABΠ使得evaluation problem算得的機率盡量大。

更新的原理，採用了「maximum likelihood estimation」，以樣本平均數作為分布平均數，出現這些樣本的機率就是最大。

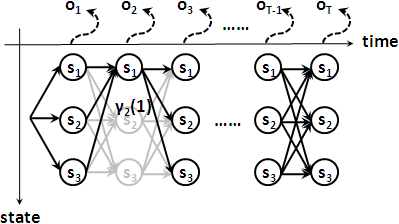
分子是穿越狀態sᵢ的所有路徑的機率的總和：

              αₜ(i) × βₜ(i)
γₜ(i) = ————————————————————————— = ∑j=1⋯N ξₜ(i,j)
         ∑i=1⋯N [ αₜ(i) × βₜ(i) ]

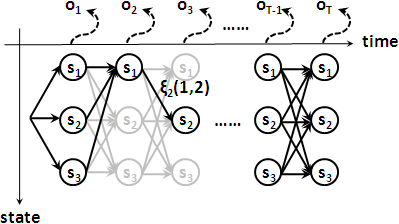
分子是穿越邊aᵢⱼ的所有路徑的機率的總和：

                  αₜ(i) × aᵢⱼ × bⱼ(ot+1) × βt+1(j)
ξₜ(i,j) = —————————————————————————————————————————————————
           ∑i=1⋯N ∑j=1⋯N [ αₜ(i) × aᵢⱼ × bⱼ(ot+1) × βt+1(j) ]

更新：

πᵢ    = γ₁(i)
aᵢⱼ   = ∑t=1⋯T-1 [ ξₜ(i,j) ] ÷ ∑t=1⋯T-1 [ γₜ(i) ]
bⱼ(k) = ∑t=1⋯T, oₜ=k [ γₜ(i) ] ÷ ∑t=1⋯T [ γₜ(i) ]

const int N = 3, M = 3, T = 15; double π[N], a[N][N], b[N][M]; // HMM double α[T][N], β[T][N]; // evaluation problem double δ[T][N]; int ψ[T][N]; // decoding problem double γ[T][N], ξ[T][N][N]; // training problem void learn(int* o, int T) { forward(o, T); backward(o, T); for (int t=0; t<T; ++t) { double p = 0; for (int i=0; i<N; ++i) p += α[t][i] * β[t][i]; assert(p != 0); for (int i=0; i<N; ++i) γ[t][i] = α[t][i] * β[t][i] / p; } for (int t=0; t<T-1; ++t) { double p = 0; for (int i=0; i<N; ++i) for (int j=0; j<N; ++j) p += α[t][i] * a[i][j] * b[j][o[t+1]] * β[t+1][j]; assert(p != 0); for (int i=0; i<N; ++i) for (int j=0; j<N; ++j) ξ[t][i][j] = α[t][i] * a[i][j] * b[j][o[t+1]] * β[t+1][j] / p; } // 更新Π for (int i=0; i<N; ++i) π[i] = γ[0][i]; // 更新A for (int i=0; i<N; ++i) { double p2 = 0; for (int t=0; t<T-1; ++t) p2 += γ[t][i]; assert(p2 != 0); for (int j=0; j<N; ++j) { double p1 = 0; for (int t=0; t<T-1; ++t) p1 += ξ[t][i][j]; a[i][j] = p1 / p2; } } // 更新B for (int i=0; i<N; ++i) { double p[M] = {0}, p2 = 0; for (int t=0; t<T; ++t) { p[o[t]] += γ[t][i]; p2 += γ[t][i]; } assert(p2 != 0); for (int k=0; k<M; ++k) b[i][k] = p[k] / p2; } }

延伸閱讀：取log

寫程式時，機率都是小於一的數字，連乘之後數字越來越小。然而，計算機的浮點數，精確度是有極限的，當T很大時，連乘之後那就變成零了。所以實作時我們會取log，連乘也就變成了連加，避免連乘之後變成零的窘境。

舉例來說，一條路徑的機率，取log之後，可以寫成：log( π_q₁ × a_q₁q₂ × b_q₁( o₁ ) × ...... ) = log( π_q₁ ) + log( a_q₁q₂ ) + log( b_q₁( o₁ ) ) + ......。預先把ABΠ的每個數值取log即可。

取log之後，處理decoding problem沒有什麼大問題，比較麻煩的是evaluation problem與training problem，除了乘法運算還有加法運算。實數乘法化作了log加法，那麼實數加法怎麼辦呢？可以使用下列公式：

利用log(p)與log(q)，求出log(p+q)，一般讓底數等於10。b可以是任意數。

if p ≥ q
  logb (p + q)  = log p + logb (1 + blogb q - logb p)
else
  logb (p + q)  = log q + logb (1 + blogb p - logb q)

知名的隱藏馬可夫模型套件HTK是這麼實作的：

#define LZERO (-1.0E10) // log(0) #define LSMALL (-0.5E10) // log values < LSMALL are set to LZERO #define minLogExp -log(-LZERO) // ~=-23 double LogAdd(double x, double y) { double temp, diff, z; if (x < y) { temp = x; x = y; y = temp; } diff = y-x; // notice that diff <= 0 if (diff < minLogExp) // if y' is far smaller than x' return (x < LSMALL) ? LZERO : x; else { z = exp(diff); return x + log(1.0 + z); } }

延伸閱讀：smoothing

training problem針對沒出現的觀察值，更新之後機率是零。往後，evaluation problem與decoding problem針對此觀察值，算得機率均是零。也就是說，一旦變成零，就無法恢復成非零了。

更新為零，可以改成更新為一個很小但是不等於零的數字，記得維持機率總和等於一。

只有離散版本HMM有此問題，稍後介紹的連續版本HMM就無此問題。

classification

   兩組調性不同的資料集
   data set 1    data set 2
1. ABBCABCAABC   BBBCCBC
2. ABCABC        CCBABB
3. ABCAABC       AACCBBB
4. BBABCAB       BBABBAC
5. BCAABCCAB     CCAABAB
6. CACCABCA      BBBCCBAA
7. CABCABCA      ABBBBABA
8. CABCA         CCCCC
9. CABCA         BBAAA

每一個資料集各自建立一個HMM，實施training problem，訓練旗下所有資料。每筆資料輪流訓練一次，然後循環L次。

如果不是輪流訓練，而是連著訓練L次，那麼HMM熟記了後面幾個，反而淡忘了前面幾個。

const int N = 3, M = 3, T = 15, L = 20; struct HMM { double π[N], a[N][N], b[N][M]; double forward(int* o, int T); double backward(int* o, int T); double decode(int* o, int T, int* q); void learn(int* o, int T); } hmm[2]; // 每個HMM可以共用的記憶體。 double α[2][N], β[2][N]; // evaluation problem double δ[2][N]; int ψ[T][N]; // decoding problem double γ[T][N], ξ[T][N][N]; // training problem void train(string dataset[2][9]) { for (int i=0; i<2; ++i) for (int l=0; l<L; ++l) for (int j=0; j<9; ++j) { // 把資料轉換成離散數值。最好可以預先轉換好。 int o[T]; for (int k=0; k<dataset[i][j].size(); ++k) o[k] = dataset[i][j][k] - 'A'; hmm[i].learn(o, dataset[i][j].size()); } }

如果每筆資料是不定期收到的、訓練好的HMM隨時要用於辨識，就無法輪流訓練。解決方式是記住之前的training problem表格，以比重求得這次training problem的平均數。

          1 × γ₁(i) + n × γ₁(n)(i)
πᵢ(n+1) = ——————————————————————————
                   1 + n

           1 × ∑t=1⋯T-1 [ ξₜ(i,j) ] + n × ∑t=1⋯T-1 [ ξₜ(n)(i,j) ]
aᵢⱼ(n+1) = ——————————————————————————————————————————————————————
               1 × ∑t=1⋯T [ γₜ(i) ] + n × ∑t=1⋯T [ γₜ(n)(i) ]

             1 × ∑t=1⋯T, oₜ=k [ γₜ(i) ] + n × ∑t=1⋯T, oₜ=k [ γₜ(n)(i) ]
bⱼ(n+1)(k) = ———————————————————————————————————————————————————————
                  1 × ∑t=1⋯T [ γₜ(i) ] + n × ∑t=1⋯T [ γₜ(n)(i) ]

pattern recognition

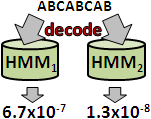
訓練好的HMM馬上可用於辨識。要辨識一筆資料，就窮舉每一個HMM，看看該筆資料最符合哪個HMM。所謂最符合，就是實施evaluation problem，取機率最大者，作為辨識結果。

為了加速，通常改用decoding problem。取log的情況下，evaluation problem要處理對數相加，而decoding problem不必，因此decoding problem效率略勝一籌。

經實驗觀察，採用evaluation problem與採用decoding problem的辨識結果幾乎相同。至于你信不信，我反正信了。

int recognize(int* o, int T) { int ans = -1; double p = -1e9; for (int i=0; i<2; ++i) { double pp = hmm[i].decode(o, T, q); if (pp > p) p = pp, ans = i; } return ans; }

ICPC 6147

Gaussian mixture model

之前說，每個狀態都會噴出M種固定的值。然而現實生活中，觀察值通常是實數，也通常有誤差，不見得恰好就是這M種值。

一個直覺的解決方案是假設誤差呈常態分布：以常態分布的平均數μ，代表正確的噴出數值；以常態分布的變異數σ²，控制誤差範圍。M個觀察值分別製作M個常態分布，標作N( v , μ₁ , σ₁² )到N( v , μ_M , σ_M² )。

狀態不再噴出k種值，而是有k種噴出管道。觀察值不再是固定的、離散的數值v₁到v_M，而是變動的、連續的數值v。

使用第k個噴出管道的機率，仍標作bᵢ( k )。在第k個噴出管道，噴出數值v的機率，是一個常態分布函數N( v , μₖ , σₖ² )；v代入一個實際數值，就能計算其噴出機率。

當各個常態分布的平均數很接近，或者變異數很大時，不同的噴出管道可能噴出相同數值。狀態sᵢ噴出數值v的機率，M個噴出管道都必須累計，為∑_i=1⋯M [ bᵢ( k ) × N( v , μₖ , σₖ² ) ]。

綜觀整個過程，是把M個常態分布以不同比重疊加起來，合成一個分布──此概念稱作高斯混合模型，可以應用在許多地方，連續版本的HMM便是一例。另外，通常會將bᵢ( k )重新標作cᵢₖ，以呼應加權比重的概念。

寫程式時，我們不會預先疊加起來，而是分別記錄M個常態分布的平均數和變異數。

每個狀態噴出不同的觀察值

套用高斯混合模型，觀察值從原先的離散數值變成了連續數值。換個觀點來看，套用高斯混合模型，就能製造任何一種我們想要的連續分布。

每個狀態可以使用不同平均數、不同變異數的常態分布，甚至可以使用不同數量的常態分布。狀態sᵢ使用的常態分布，標作N( v , μᵢₖ , σᵢₖ² )。

觀察值推廣到高維度

觀察值可以從一個值推廣為一個向量。其實也就是每個維度分開處理罷了。

至於training problem，則要額外更新常態分布的平均數、變異數、加權比重了：

　　　路徑第一步，穿過狀態sᵢ。
πᵢ  =  γ₁(i)

　　　分子是穿過邊aᵢⱼ。分母是穿過狀態sᵢ。
       ∑t=1⋯T-1 [ ξₜ(i,j) ]
aᵢⱼ = —————————————————————
         ∑t=1⋯T [ γₜ(i) ]

　　　分子是穿過狀態sᵢ、使用第k個噴出管道。分母是穿過狀態sᵢ。
          ∑t=1⋯T [ γₜₖ(i) ]
cᵢₖ = ————————————————————————
       ∑t=1⋯T ∑k=1⋯M [ γₜₖ(i) ]

　　　分子是穿過狀態sᵢ、使用第k個噴出管道、噴出數值的平均數。
       ∑t=1⋯T [ γₜₖ(i) ] * oₜ
μᵢₖ = ————————————————————————
          ∑t=1⋯T [ γₜₖ(i) ]

　　　分子是穿過狀態sᵢ、使用第k個噴出管道、噴出數值的共變異矩陣。
       ∑t=1⋯T [ γₜₖ(i) ] * (oₜ - μᵢₖ)(oₜ - μᵢₖ)T
Σᵢₖ = ——————————————————————————————————————————
                  ∑t=1⋯T [ γₜₖ(i) ]

至此產生了連續版本的HMM，已經可以應付各種情況了！

總結

未知輸入、未知函數、只知輸出，求輸入。

輸入是Markov chain、函數是HMM、輸出是數列。

針對一個已知的輸出數列，我們調整函數，讓該輸出數列的出現機率最大，同時求出機率多寡。（理論上應該要同時考慮所有輸出數列，讓整體的機率最大；但是這樣時間複雜度太高是指數時間，只好一次處理一個。）

針對一個新的輸出數列，我們找到可能性最高的輸入數列，同時求出機率多寡。

另外HMM可以用來分類數列。每一種類別，各自建立一個HMM。針對一個新的輸出數列，以機率多寡來判斷其分類。