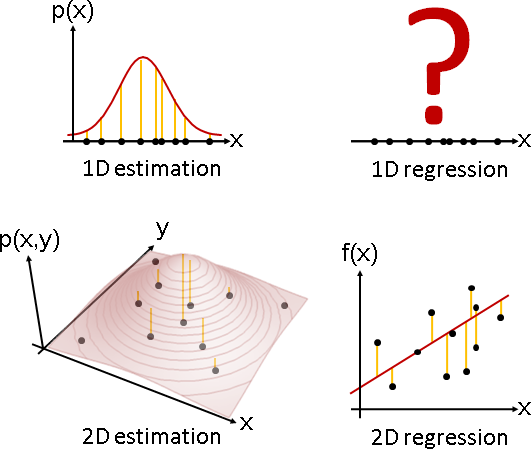
estimation（parameter estimation）

「估計」就是選定一種分布（例如常態分布、二項式分布、gamma分布），找到適當的參數（例如平均數、變異數、形狀參數），盡量符合手邊的一堆樣本。

「估計」也是迴歸，函數改成機率密度函數，函數點改成樣本。

Plot3D[PDF[MultinormalDistribution[{0, 0}, {{1, 0}, {0, 1}}], {x, y}], {x, -2, 2}, {y, -2, 2}, Boxed -> False, Axes -> False, Mesh -> Automatic, MeshFunctions -> {#3&}]

estimator

以函數進行迴歸，所謂最符合就是誤差最小，讓所有函數點的誤差總和盡量小，例如least squares。

以分布進行估計，所謂最符合就是機率最大，讓所有樣本的機率總乘積盡量大，例如maximum likelihood、maximum a posterior。

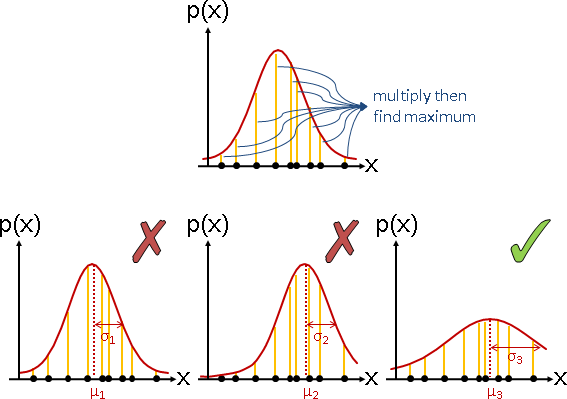
一、已知樣本，欲求分布的參數。
二、首先嘗試直接法，以樣本直接推導參數。
　　然而十分困難，無法得到數學公式。
三、於是嘗試試誤法，窮舉參數的各種可能數值，一一驗證。
　甲、針對一種數值：
　　回、採用ML：各個樣本一一代入分布、一一求得機率。
　　　　採用MAP：再乘上該分布參數的出現機率。
　　回、求得所有樣本的機率總乘積。
　乙、窮舉各種可能數值：
　　回、以機率總乘積最大者，推定為正確參數。
　　回、機率總乘積，可以取log，連乘化作連加。
　　　　以避免機率越乘越小、低於浮點數精確度而變成零。
　　　　（取log之後，最大值位置不變。）
四、窮舉法太慢，於是嘗試其他的最佳化演算法。
　　例如EM algorithm、牛頓法。

範例：店面一日人潮統計

我準備好筆記本、手錶、提神飲料，從半夜12點開始，坐在麵店門口24小時，痴痴地等著客人上門，登記每位客人的到訪時間，作為樣本。我認為到訪時間呈gamma分布，我想估計平均數和形狀參數是多少。

【待補圖片】

平均數可能是0點、1點、2點、……、24點，看起來每一種都有可能。這個時候就應該使用maximum likelihood。

【待補圖片】

不過根據我對真實世界的了解，我知道大家通常晚上六點下班，然後大家相約吃飯小酌一下。所以平均數是19點、20點、21點、22點的機率非常高！我也知道三更半夜，不太有人吃麵，所以平均數是2點、3點、4點的機率非常低！我認為平均數呈常態分布！這個時候就應該使用maximum a posterior。

【待補圖片】

estimation數學式子

以統計學慣用的代數符號，重新說明「估計」。

一、已知一堆樣本X = {x₁, ..., xₙ}。
　　已知特定分布的機率密度函數f(x, μ, σ², λ)。
　　不知特定分布的參數Θ = {μ, σ², λ, ...}，
　　像是機率密度函數的平均數μ、變異數σ²、形狀參數λ、……

二、已知與未知，寫成條件機率。

　　p( μ,σ,λ,... | x₁,...,xₙ,f ) 或者 p( Θ | X,f )

三、所謂最符合，就是機率最大。

　　max p( μ,σ²,λ,...  | x₁,...,xₙ,f ) 或者 max p( Θ | X,f )

四、找到此時平均數μ、變異數σ、形狀參數λ是多少。

　　argmax p( μ,σ²,λ,... | x₁,...,xₙ,f ) 或者 argmax p( Θ | X,f )
　　μ,σ²,λ,...                                  Θ

五、求得函數 p( Θ | X,f ) 的最大值，以及最大值所在位置。
　　雖然我們知道p函數一定存在，但是我們不知道p函數長什麼樣，無從計算。
　　只好改用ML或MAP。

maximum likelihood：找到其中一種分布參數，在此參數下，各個樣本的機率，乘積最大。

一、找到其中一種分布參數，在此參數下，這堆樣本的出現機率最大。

　　argmax f(X|Θ)
　　  Θ

二、推定樣本之間互相獨立（不互相影響、隨機取得），就可以套用乘法定理。

　　argmax f(X|Θ)
　　  Θ
　= argmax [ f(x₁|Θ) ⋅ ... ⋅ f(xₙ|Θ) ]
　　  Θ

三、取 log 將連乘化作連加。取 log 後最大值位置仍相同。

　　argmax log f(X|Θ)
　　  Θ
　= argmax log [ f(x₁|Θ) ⋅ ... ⋅ f(xₙ|Θ) ]
　　  Θ
　= argmax     [ log f(x₁|Θ) + ... + log f(xₙ|Θ) ]
　　  Θ

四、求得函數log f(X|Θ)的最大值，以及最大值所在位置。

maximum a posterior：找到其中一種分布參數，讓各個樣本、各個分布參數的機率，乘積最大。

一、找到其中一種分布參數，這堆樣本暨分布參數的出現機率最大。

　　argmax p(X,Θ)
　　  Θ

二、套用貝氏定理。

　　argmax p(X,Θ) = argmax { p(X|Θ) ⋅ p(Θ) }
　　  Θ               Θ

三、推定樣本之間互相獨立（不互相影響、隨機取得），就可以套用乘法定理。

　　argmax p(X,Θ) = argmax { p(X|Θ) ⋅ p(Θ) }
　　  Θ               Θ
　= argmax { f(x₁|Θ) ⋅ ... ⋅ f(xₙ|Θ) ⋅ p(Θ) }
　　  Θ

四、後面步驟如法炮製。只多了一項 p(Θ)。

　　argmax log p(X,Θ) = argmax log { p(X|Θ) ⋅ p(Θ) }
　　  Θ                   Θ
　= argmax log { f(x₁|Θ) ⋅ ... ⋅ f(xₙ|Θ) ⋅ p(Θ) }
　　  Θ
　= argmax     { log f(x₁|Θ) + ... + log f(xₙ|Θ) + log p(Θ) }
　　  Θ

五、求得函數log p(X,Θ)的最大值，以及最大值所在位置。

ML是MAP的特例。ML假設各種分布參數的出現機率均等，呈uniform distribution。MAP更加仔細考慮分布參數的出現機率，不見得要均等。

演算法（expectation–maximization algorithm）

專為ML和MAP設計的最佳化演算法，找到機率最大值。

http://www.seanborman.com/publications/EM_algorithm.pdf
http://www.cs.cmu.edu/~awm/10701/assignments/EM.pdf
https://ibug.doc.ic.ac.uk/media/uploads/documents/expectation_maximization-1.pdf

一、凹函數定義可以寫成加權平均：加權平均之後函數值必然上升。
　　註：凹函數的外觀是凸的。
二、機率函數的期望值，就是加權平均！
　　如果機率函數是凹函數，
　　想求極值，那就好辦，不斷求期望值即可！
三、改變ML函數、移動log位置，變成一個凹函數。
　　證明此凹函數小於等於原式，是ML函數的下界。
四、凹函數求期望值、往上爬，函數值嚴格上升。
　　ML函數的函數值必然同時跟著上升。
五、根據現在位置，
　　不斷求一個新的凹函數，不斷求期望值、往上爬。
　　最後就會得到局部極值，類似hill climbing演算法。

以統計學慣用的代數符號，此演算法利用貝氏定理，對調主角配角，重算加權平均。

【待補文字】

https://www.ptt.cc/bbs/Math/M.1570515880.A.029.html

bias / variance

我要怎麼知道一開始選擇的estimator是對的？我要如何判斷estimator是否適合用於該分布呢？

bias是指「窮舉各種樣本組成，分別估計參數，所有結果的平均數」與「真實參數」的差值。

bias是衡量估計參數對不對的指標。不好的estimator，可以證明估計參數鐵定失準。

variance就是變異數，此處我們是算「窮舉各種樣本組成，分別估計參數，所有結果的變異數」。

variance此處用來衡量估計參數的浮動範圍。我們希望對於奇葩的樣本組成，估計結果仍然差不多，浮動範圍越小越好。

bias和variace是兩件事情。即便正確，還是可以有浮動範圍。

仔細推導bias和variance的關係式。平方誤差的平均數，由bias和variance組成。完美的估計，令平方誤差達到極小值、為定值，而此時bias和variance此消彼長，魚與熊掌不可兼得。

mean square error = (bias)² + variance

儘管我們不可能知道真實參數是多少，不過卻可以得到魚與熊掌不可兼得的結論：無論採用哪種estimator，bias和variance無法同時令人滿意。

數學公式（sample mean / sample variance）

運氣差，套用最佳化演算法。運氣好，直接推導公式解。

經典的分布，諸如常態分布、二項式分布，估計參數時採用ML，恰好可以推導公式解：極值位於一次微分等於零的地方。

平均數的公式解稱作「母體平均數」，變異數的公式解稱作「母體變異數」。母體二字常省略。

μ = (x₁ + ... + xₙ) / n
σ² = [ (x₁ - μ)² + ... + (xₙ - μ)² ] / n

ML用於估計平均數沒有問題，其bias等於零。不必補救。

ML用於估計變異數時不可靠，其bias不是零。補救方式是將分母改成n-1，其bias才是零。證明省略。

補救版本稱作「樣本平均數」、「樣本變異數」。

x̄ = (x₁ + ... + xₙ) / n
s² = [ (x₁ - x̄)² + ... + (xₙ - x̄)² ] / (n-1)

數學公式（law of large numbers）

大數定律：當樣本無限多、樣本互相獨立，則母體平均數趨近分布平均數。

當樣本無限多，除了透過「maximum likelihood」與「極值位於一次微分等於零的地方」來推導平均數公式解，也可以透過大數定律來獲得平均數公式解。

只有經典的分布，才能順利的移項求解，相當麻煩。但是任意的分布，都能套用大數定律，相當方便。

真實世界當中，不存在「樣本無限多」，只好「樣本足夠多」。多少才叫足夠多？這屬於統計學的範疇，就此打住。

母體變異數（或者樣本變異數）趨近分布變異數，這部分我查不到任何資料。

model selection / model validation

我要怎麼知道一開始選擇的分布是對的？我要如何判斷到訪時間比較像gamma分布，或者比較像Poisson分布呢？

似乎大家都是自由心證。這屬於統計學的範疇，就此打住。

AIC = -2ln(likelihood) + 2k
BIC = -2ln(likelihood) + k⋅ln(N)
k = model degrees of freedom
N = number of observations

normal distribution

機率論課程有教，就不多介紹了。

           exp(-(k-μ)² / 2σ²)
P(X = k) = ——————————————————
                sqrt(2σ²)

若選定「normal distibution」進行估計，參數μ為樣本平均數，參數σ²為樣本變異數。

linear regression with normal error

一次迴歸，迴歸函數添上誤差項，誤差項推定為常態分布。此即訊號學的「additive white Gauss noise」。

現在要盡量符合樣本。由於迴歸函數含有常態分布，只好從迴歸改為估計，採用maximum likelihood。

由於是經典分布，式子漂亮，得直接運用「一次微分等於零」，推導公式解。

可以發現：添加誤差項、採用maximum likelihood實施估計，未添加誤差項、採用least squares實施迴歸，兩者結果恰好一致！

也就是說：普通的一次迴歸，已經內建「誤差項呈常態分布」的效果！我們直接實施普通的一次迴歸即可，大可不必設定誤差項，自尋煩惱。

網路上有人把這件事情解讀成：maximum likelihood是least squares的通例。雖然不那麼正確，但是也不能說完全錯誤。

normal regression

換個觀點解釋方才的事情。

一、每個樣本，最後一個維度，由不同的 1D normal distribution 產生。
　　每個樣本，前面幾個維度，用於各個 1D normal distribution 的平均數 μ。
二、推定各個 1D normal distribution 的平均數 μ 呈線性成長。
　　μ = ax + b
三、推定各個 1D normal distribution 的變異數 σ² 皆相同。
四、已知樣本們 (xᵢ, yᵢ)，求得參數 a b。採用ML。
　　argmin prod P(X = yᵢ ; μ = axᵢ + b, σ² = constant)
　　 a,b    i

2D sample: (x, y)        -->  μ = ax + b
3D sample: (u, v, y)     -->  μ = au + bv + c
4D sample: (u, v, w, y)  -->  μ = au + bv + cw + d

迴歸函數是一次函數，代表各個常態分布的平均數。

為何我們迫令變異數皆相同呢？N+1個關係式（N個樣本、平均數呈線性成長）、N+1個未知數（N種平均數、一種變異數），得到唯一解。

log-linear model

一次函數進行迴歸，容易推導公式解。於是統計學家以一次函數為基礎，產生各種函數。

此處要使用的是log-linear model，取log之後是一次函數。

y = exp(ax + b) , log(y) = ax + b

Poisson distribution

機率論課程有教，就不多介紹了。

P(X = k) = λᵏ exp(-k) / k!

若選定「Poisson distibution」進行估計，參數λ為樣本平均數。

Poisson regression

一、每個樣本，最後一個維度，由不同的 1D Poisson distribution 產生。
　　每個樣本，前面幾個維度，用於各個 1D Poisson distribution 的平均數 λ。
二、推定各個 1D Poisson distribution 的平均數 λ 呈指數成長。
　　λ = exp(ax + b)
三、已知樣本們 (xᵢ, yᵢ)，求得參數 a b。採用ML。
　　argmin prod P(X = yᵢ ; λ = exp(axᵢ + b))
　　 a,b    i

2D sample: (x, y)        -->  λ = exp(ax + b)
3D sample: (u, v, y)     -->  λ = exp(au + bv + c)
4D sample: (u, v, w, y)  -->  λ = exp(au + bv + cw + d)

Poisson regression推定平均數呈指數成長，符合真實世界的常見情況。當然也可以更換成別種成長方式。

演算法

【待補文字】

logistic function

「logistic function」初始成長緩慢、中途成長迅速、飽和成長緩慢，是真實世界的常見情況。

「logit function」是其反函數。

中文翻譯非常奇葩，沒有一個是符合原義的。

logistic：名稱源自古代數學名詞「logistic number比值」。意義源自指數與對數。

翻譯形形色色。狀似logic而譯作「邏輯」。狀似logarithmic而譯作「對數」。狀似人名而譯作「羅吉斯」。仿照logic的翻譯方式而譯作「逻辑斯谛」。

logit：原創詞彙，參考了「probit」這個字。

翻譯林林總總。狀似logic而譯作「邏輯」。狀似log而譯作「對數勝算」。狀似人名而譯作「羅吉特」。不知為何而譯作「分數對數」、「分对数」。

順帶一提，「logistics物流」是之後才出現的詞彙，其起源跟這兩個單字無關。不過logistic function恰好非常符合物流進度。

Bernoulli distribution

擲一次硬幣，正面機率p，反面機率1-p。

P(X = 1) = p
P(X = 0) = 1-p

若選定「Bernoulli distribution」進行估計，參數p為樣本平均數。注意到：樣本數值只能是0或1。

Bernoulli regression（logistic regression）

一、每個樣本，最後一個維度，由不同的 1D Bernoulli distribution 產生。
　　每個樣本，前面幾個維度，用於各個 1D Bernoulli distribution 的出現機率 p。
二、推定各個 1D Bernoulli distribution 的出現機率 p 呈logistic成長：
　　p = 1/(1+exp(-(ax+b)))
　　另一種等價解釋，推定其勝算（odds）呈指數成長：
　　p/(1-p) = exp(ax + b)
　　另一種等價解釋，推定其logit function呈線性成長：
　　log(p/(1-p)) = ax + b
三、已知樣本們 (xᵢ, yᵢ)，求得參數 a b。採用ML。
　　argmin prod P(X = yᵢ ; p = 1/(1+exp(-(axᵢ+b))))
　　 a,b    i

logistic regression推定平均數呈logistic成長，以便將數據粗略分成兩類，一類較高、一類較低。

演算法

採用maximum likelihood，經過偏微分，可以找到某兩個式子成立時，有最大值。

此二式難以推導公式解，故採用最佳化演算法Newton's method。

int x[10], y[10]; double a, b; double p(int i, int d) { double t = exp(a + b * x[i]); if (d == 0) return 1 - 1 / (1 + t); else if (d == 1) // d/da return t / ((1+t)*(1+t)); else // d/db return x[i]*t / ((1+t)*(1+t)); } double f(int k, int d) { double res = 0; for (int i = 0; i < 10; i++) res += (p(i, d) - (d==0?y[i]:0)) * (k==0?1:x[i]); return res; } void logistic_regression() { // x0 a = 0; b = 0; for (int k = 0; k < 50; k++) { // Jacobian matrix double J[2][2] = { { f(0,1), f(0,2) }, { f(1,1), f(1,2) } }; // Jacobian matrix inverse double det = J[0][0] * J[1][1] - J[0][1] * J[1][0]; double invJ[2][2] = { { J[1][1]/det, -J[1][0]/det }, { -J[0][1]/det, J[0][0]/det } }; // xn+1 = xn - inv(J(x)) * F(x) double F[2] = { f(0,0), f(1,0) }; a -= (invJ[0][0] * F[0] + invJ[0][1] * F[1]); b -= (invJ[1][0] * F[0] + invJ[1][1] * F[1]); } cout << a << b; }

UVa 10727

Gauss process regression（kriging）

多項式內插，引入機率的概念，讓內插函數擁有浮動範圍。