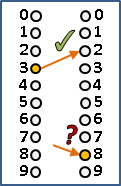linear function

「線性函數」。加權總和函數。

f(x₁, x₂, ..., xₙ) = w₁ x₁ + w₂ x₂ + ... + wₙ xₙ

線性函數是計算機科學經常使用的函數，熱門程度遠勝二元樹。現實世界相當複雜，經常出現難以計算的事物，此時工程師就會將事情簡化為線性函數。線性函數擁有強悍的數學性質和演算法，儘管艱深晦澀，但是質樸實用。

詳情請見本站文件「linear function」。

stochastic function

「隨機函數」。輸入是浮動數字。輸出顯然也是浮動數字。

f(X, Y, Z) = a X + Y Z     where X, Y, Z are random variable

古代數學家沒有仔細區分「浮動：有規矩」和「隨機：無規矩」的差別，把兩者都命名為隨機，混淆視聽。大家搞不清楚狀況的情況下，stochastic function跟random function被當作相同。

random function

「隨機函數」。輸入輸出隨機對應的函數。

隨機函數的輸入輸出，可以是連續數字、也可以是離散數字。

電腦做運算，數值皆離散。我們只能處理離散數字。

初次建立隨機函數，對應方式是隨機的；每次使用隨機函數，對應方式是固定的。

如果對應方式每次都是隨機的，那麼其實就是隨機數了。

// 產生隨機函數。輸入範圍[0,x)、輸出範圍[0,y)。 void make_random_function(int f[], int x, int y) { // 針對每一種輸入，產生[0,y)的隨機整數，作為輸出。 srand(time(0)); for (int i=0; i<x; ++i) f[i] = rand() % y; }

隨機函數是計算機科學的核心思想之一，經典程度堪比二元樹。例如稍後提到的hash function，其中一種變種就是均勻隨機函數，可以使用在伺服器負載平衡、網路資料庫存取。

random permutation

「隨機排列」。一對一隨機函數。

利用下個小節的演算法，來製造隨機排列。

// 產生隨機排列。輸入範圍[0,n)、輸出範圍[0,n)。 void make_random_permutation(int f[], int n) { for (int i=0; i<n; ++i) f[i] = i; random_permutation(f, n); // 請見下個小節 }

隨機排列是計算機科學的核心思想之一，經典程度堪比二元樹。隨機排列是加密演算法的基礎，加密演算法是網路傳輸的基礎，網路傳輸是上網閱讀文章、觀看影片的基礎。

random permutation（random shuffle）

方才是函數，此處是數列。

「隨機排列」或「隨機混洗」。兩種解讀方式：

一、所有排列挑出一種排列。機率都一樣。

二、一群數字不按順序排好、打亂順序。排序的相反。

隨機排列可以用於製造隨機輸入，用來測試程式是否穩健。隨機排列也可以用來製作視覺特效。

演算法是Fisher–Yates shuffle：跟後方任意數字交換、或者不交換。時間複雜度O(N)。

可以直接使用C++標準函式庫的shuffle()。

// 產生[0,x)的隨機整數。注意到x不能大於RAND_MAX。 int rand(int x) { return rand() % x; } // 產生[x,y)的隨機整數。 int rand(int x, int y) { return x + rand(y - x); } void random_permutation(int a[], int N) { // 設定亂數表，之後才能使用rand()。 srand(time(0)); for (int i=0; i<N-1; i++) swap(a[i], a[ rand(i, N) ]); } void random_permutation(int a[], int N) { srand(time(0)); for (int i=N-1; i>0; i--) // 倒過來做，省略一個參數。 swap(a[i], a[ rand() % (i+1) ]); }

random k-combination（simple random sampling）

「隨機k組合」或「簡單隨機抽樣」。兩種解讀方式：

一、所有組合挑出一種組合，其大小為k。機率都一樣。

二、一群數字打亂順序，然後挑出前k個數字。

演算法是reservoir sampling：依序讀取數字，取代當下組合的任意數字，或者不取代。online演算法，當下組合是當下答案。時間複雜度O(N)。

改良版本是Li's algorithm：跳躍讀取數字，節省時間。背後原理是幾何分布。時間複雜度O(K + Klog(N/K))，到達理論下限。

可以直接使用C++標準函式庫的sample()。

vector<int> random_combination(int a[], int N, int K) { srand(time(0)); vector<int> comb(K); for (int i=0; i<K; i++) comb[i] = a[i]; for (int i=K; i<N; i++) { int j = rand() % i; if (j < K) comb[j] = a[i]; } return comb; } vector<int> random_combination(int a[], int N, int K) { default_random_engine g; uniform_int_distribution<int> rand(0, K-1); uniform_real_distribution<double> uniform(0, 1); vector<int> comb(K); for (int i=0; i<K; i++) comb[i] = a[i]; double W = exp(log(uniform(g))/K); for (int i=K; i<N; i++) { i += floor(log(uniform(g))/log(1-W)); if (i >= N) break; comb[rand(g)] = a[i]; W *= exp(log(uniform(g))/K); } return comb; }

hash function

「雜湊函數」。限制輸出範圍的函數。

雜湊函數有著形形色色的變種：限寬、均勻、保距、量化、混亂、單向、編碼。大家視情況需要，混用多個變種。

hash是一種菜式：肉、馬鈴薯、蔬菜，剁碎攪拌成為餡泥，然後烤炸。hash具有諸多意涵：均勻隨機、範圍壓縮、型態變化。

1. hash function

限寬。限制輸出範圍。簡易方式是mod運算。

用途是縮減數字範圍。

int hash(int n) { return n % 10; // 輸出範圍是整數[0,9]。 } // C++標準函式庫的hash // 印出數字100的雜湊值 hash<int> h; cout << h(100);

2. uniform hash function

均勻。輸出數字使用機率均等。簡易方式是mod最大公因數。

用途是均勻分散儲存。知名應用是hash table。

3. isometric mapping / locality-sensitive hashing

保距。所有數對，變換前的差異，大致等於變換後的差異。簡易方式是線性變換。

同樣道理，還可以發明保長、保角、保秩、保序等變種。

用途是以雜湊值估計相似度。

4. quantization / projection

量化。刪除數字的細節，降低精確度。簡易方式是floor運算。

用途是簡化數字。知名演算法是PCA、KNN。

int hash(int n) { return n / 10 * 10; // 刪除個位數 }

5. random hash function

混亂。輸出是固定的隨機數。簡易方式是以輸入數字生成隨機數、隨機排列。

// linear congruential generator int hash(int n) { // 輸出是隨機數，位於[0, 2³¹-1]。 unsigned int hash = n; hash = hash * 1103515245U + 12345U; return int(hash % 2147483648U); }

6. one-way hash function

單向。難以從輸出推算輸入。簡易方式是餘數連乘、三角函數。

用途是密碼、摘要、簽章，讓外人難以偽造變換前的原始資料。知名演算法如SHA-2、MD5。

請見本站文件「encryption」。

7. coding / indexing

編碼。輸入不是數字，而是其他元件，例如字串。簡易方式是先化作多項式、再化作數字。

用途是建立索引表，知名演算法如murmur、xxHash。

請見本站文件「string」。

// 印出浮點數0.123的雜湊值 cout << hash<float>{}(0.123f); // 印出字串abc的雜湊值 cout << hash<string>{}("abc");

comparison function【尚無正式名稱】

「比較函數」。比較兩個元件。輸出是布林數。

例如實數運算之大於、小於、等於。

less-than function
f(x, y) = ⎰ true,   if x < y
          ⎱ false,  otherwise

bool less_than(int x, int y) { return x < y; }

例如集合運算之屬於、等於。

element-of function
f(x, A) = ⎰ true,   if x ∈ A
          ⎱ false,  otherwise

bool element_of(int x, vector<int> A) { for (int i=0; i<(int)A.size(); ++i) if (x == A[i]) return true; return false; }

Iverson function

「艾佛森函數」。布林數轉成實數。輸入是布林數。

另有數學符號Iverson bracket，可以縮短數學式子。

Iversion function
f(x) = ⎰ 1,  if x is true     f(x) = [x]
       ⎱ 0,  otherwise

(conditional equation)        (Iverson bracket)

int a = true; // C++自動將bool隱性轉型成int // C的bool其實就是int // 沒有人這樣寫 int iverson(bool x) { return x; }

conditional function【尚無正式名稱】

「條件函數」。函數內含比較函數與艾佛森函數。

條件函數主要用來設計計算流程，尤其是程式語言與演算法。不僅是計算機科學，各種科學、各種工程都會偶爾使用它們。

indicator function
IA(x) = ⎰ 1,  x ∈ A             I(x; A) = [x ∈ A]
        ⎱ 0,  otherwise

Kronecker delta function
δ(x; y) = ⎰ 1,  x = y           δ(x; y) = [x = y]
          ⎱ 0,  otherwise

threshold function
thr(x; y) = ⎰ 1,  x ≥ y         thr(x; y) = [x ≥ y]
            ⎱ 0,  otherwise

sign function
sgn(x) = ⎧ -1,  x < 0
         ⎨  0,  x = 0
         ⎩  1,  x > 0

absolute value function
abs(x) = ⎰ -x,  x < 0
         ⎱  x,  x ≥ 0

minimum function
min(x, y) = ⎰ x,  x < y
            ⎱ y,  otherwise

clamp function
clamp(x; [a, b]) = ⎧ a, x < a
                   ⎨ x, x ≥ a and x < b
                   ⎩ b, x ≥ b

稍微講解一下本文收錄的條件函數。

indicator function
指示函數：判斷元素是否存在。常見於數學。

Kronecker delta function
單位脈衝函數：一瞬間短暫的1。常見於數學、訊號處理。

threshold function
臨界值函數：判斷是否超過臨界值。常見於程式語言、訊號處理。

sign function
正負號函數：取得數值的正負號部分。常見於程式語言。

absolute value function
絕對值函數：取得數值的數字部分。常見於數學、程式語言。

minimum function
最小值函數：取得較小的數值。常見於數學、程式語言。

clamp function
鉗函數：取得範圍內的數值。常見於程式語言。

稍微實作一下本文收錄的條件函數。

int delta(int x, int y) {return x == y;} int thr(int x, int y) {return x >= y;} int sgn(int x) {return (x > 0) ? 1 : ((x < 0) ? -1 : 0);} int abs(int x) {return (x > 0) ? x : -x;} int min(int x, int y) {return (x < y) ? x : y;} int clamp(int x, int a, int b) {return min(max(x, a), b);}

順帶一提，分支的執行時間遠大於整數運算與布林數運算的執行時間。大家想方設法避開分支，改成整數運算、位元運算、組合語言指令。不過這不是本文主旨。

int sgn(int x) {return (x > 0) - (x < 0)}; int abs(int x) {return v * ((x > 0) - (x < 0));} int abs(int x) {int m = x >> 31; return (x ^ m) - m;} int min(int x, int y) {return y ^ ((x ^ y) & -(x < y));}

C++標準函式庫已經收錄絕大部分函數，已經想方設法降低執行時間。前人種樹後人乘涼，大可不必自己實作。

smooth function

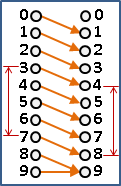
「不連續函數discontinuous function」。函數曲線上下斷開。

函數曲線不連續的地方，有兩種繪圖方式。嚴謹的方式是空心圓形和實心圓形，簡易的方式是鉛直線。

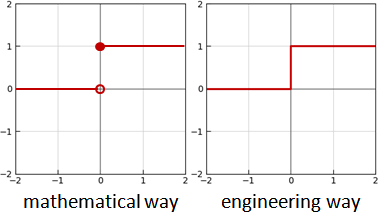
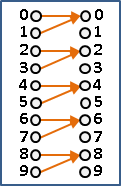
「連續函數continuous function」。處處緊密銜接。

左鄰居函數值、右鄰居函數值，兩者趨近相同。

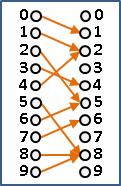
「可微函數differentiable function」。處處可以微分。

左鄰居導數值、右鄰居導數值，兩者趨近相同。

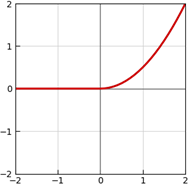
「k階可微函數Cᵏ function」。處處可以微分k次。

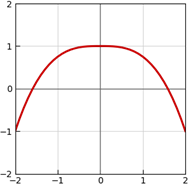
「平滑函數smooth function」。處處可以微分無限多次。

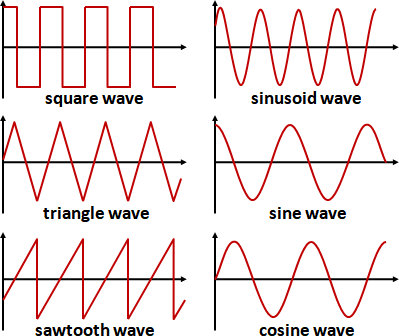
例如多項式函數（零函數、常數函數、一次函數、二次函數）、指數函數（自然指數函數）、弦型函數（正弦函數、餘弦函數）。

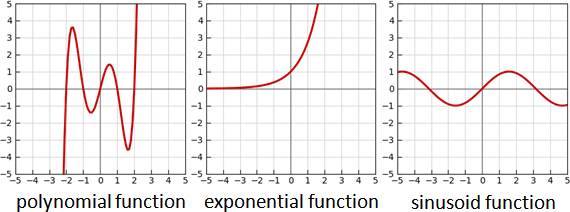
[polynomial function]
zero function                 f(x) = 0
constant function             f(x) = c
linear function               f(x) = ax + b
quadratic function            f(x) = ax² + bx + c

[exponential function]
natural exponential function  f(x) = exp(x)

[sinusoid function]
sine function                 f(x) = sin(x)
cosine function               f(x) = cos(x)

「平滑性smoothness」。函數的平滑程度。微積分是基本的函數運算。數學家利用微積分來描述平滑。數學家根據微分次數來區分平滑程度。

differentiable | name        | name
---------------+-------------+------------------------
for ≥ 0 times  | C⁰ function | continuous function
for ≥ 1 times  | C¹ function | differentiable function
:              | :           | :
for ∞ times    | C∞ function | smooth function

可微次數　　　　　　丨名稱　　　　　丨簡易名稱
一一一一一一一一一一十一一一一一一一十一一一一
處處可以微分０次以上丨零階可微函數　丨連續函數
處處可以微分１次以上丨一階可微函數　丨可微函數
　　　　：　　　　　丨　　　：　　　丨　：　　
處處可以微分無窮次　丨無窮階可微函數丨平滑函數

目前沒有詞彙可以表達「k次以下」和「恰好k次」。大家不得已沿用Cᵏ。例如Cᵏ function是「k次以上、至少k次」，Cᵏ continuity at a point是「k次以下、至多k次」，成為歷史共業。

根據微分次數，無法辨別不連續函數，成為歷史共業。

piecewise function

「分段函數」。許多段平滑函數，拼成一個函數。

分段函數主要用來設計外觀造型。不僅是計算機科學，各種科學、各種工程都會經常使用它們。

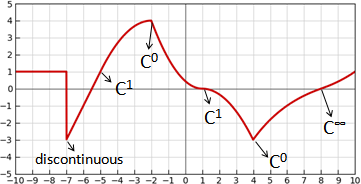
介紹三個分段函數。微分與積分恰巧得到彼此。

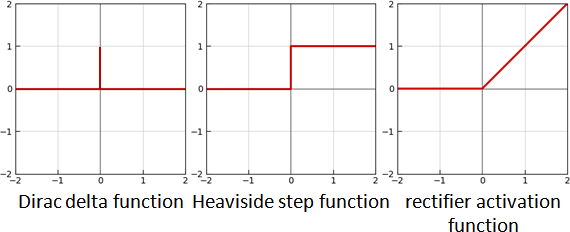
Dirac delta function
f(x) = ⎰ 1,  x = 0      f(x) = [x = 0]
       ⎱ 0,  x ≠ 0

Heavide step function
f(x) = ⎰ 0,  x < 0      f(x) = [x ≥ 0]
       ⎱ 1,  x ≥ 0

rectifier activation function (ReLU)
f(x) = ⎰ 0,  x < 0      f(x) = x [x ≥ 0]
       ⎱ x,  x ≥ 0

再介紹三個分段函數。

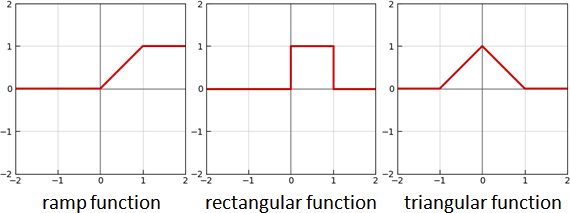
ramp function
f(x) = ⎧ 0,  x < 0
       ⎨ x,  x ≥ 0 and x < 1
       ⎩ 1,  x ≥ 1

rectangular function
f(x) = ⎧ 0,  x < 0
       ⎨ 1,  x ≥ 0 and x < 1
       ⎩ 0,  x ≥ 1

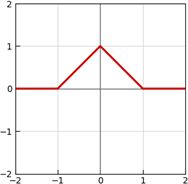
triangular function
f(x) = ⎧ 0,      x < -1
       ⎨ 1 + x,  x ≥ -1 and x < 0
       ⎪ 1 - x,  x ≥ 0 and x < 1
       ⎩ 0,      x ≥ 1

smooth approximation

「平滑近似」。分段函數，刻意改成平滑函數。

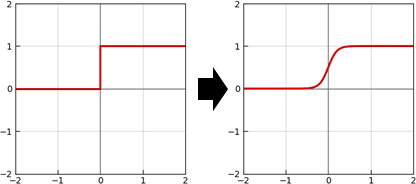
脈衝、步階、啟動的平滑近似。種類豐富，任君挑選。

自行調整x值範圍、y值範圍，以便符合分段函數曲線形狀。

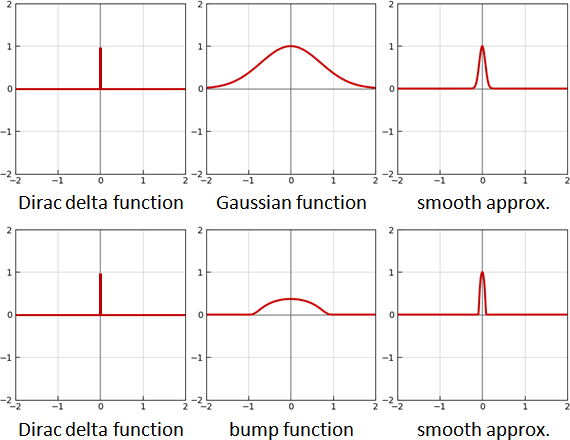
[smoothed Dirac delta function]

Gaussian function
f(x) = exp(-x²)
  ↓
f(x) = exp(-(kx)²)

bump function
f(x) = ⎰ exp(-1/(1-x²)),  -1 < x < 1
       ⎱ 0,               otherwise
  ↓
f(x) = ⎰ exp(-1/(1-(kx)²)) / exp(-1),  -1 < kx < 1
       ⎱ 0,                            otherwise

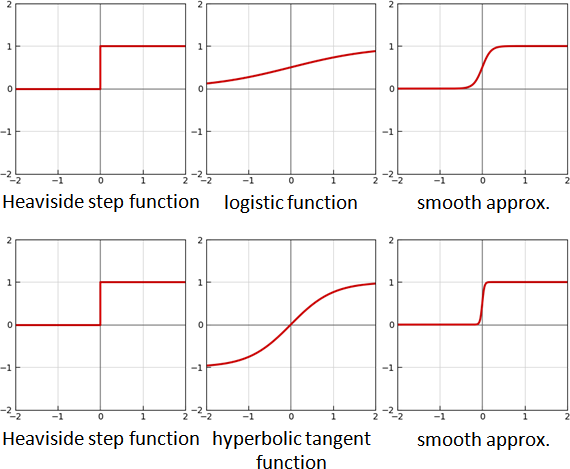
[smoothed Heaviside step function] [sigmoid]

logistic function
f(x) = 1 / (1 + exp(-x))
  ↓
f(x) = 1 / (1 + exp(-kx))

hyperbolic tangent function (tanh)
f(x) = tanh(x)
  ↓
f(x) = (tanh(kx) + 1) / 2

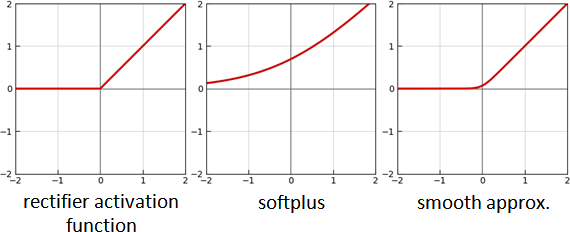
[smoothed rectifier activation function]

softplus
f(x) = log(1 + exp(x))
  ↓ 
f(x) = log(1 + exp(kx)) / k

最大值函數、箝函數的平滑近似。種類豐富，任君挑選。

[smoothed maximum function]

https://en.wikipedia.org/wiki/Smooth_maximum

smooth maximum
f(x, y) = x + y - sqrt((x - y)² + ε)

LogSumExp
f(x, y) = log(exp(x) + exp(y))

[smoothed clamp function]

smoothstep
f(x) = ⎧ 0,          x < 0
       ⎨ 3x² - 2x³,  x ≥ 0 and x < 1
       ⎩ 1,          x ≥ 1

cosine function
f(x) = ⎧ 0,                  x < 0
       ⎨ 0.5 - 0.5 cos(πx),  x ≥ 0 and x < 1
       ⎩ 1,                  x ≥ 1

spline

「樣條」。許多段內插函數，拼成一個函數。

兩個相鄰函數點，取左右鄰近函數點們做內插，只取兩個相鄰函數點之間那一段函數曲線。所有相鄰函數點，如法炮製。每一段函數曲線，一段一段接起來，形成樣條。

內插函數只能是多項式函數。大家都中邪了。

取k個函數點做多項式內插，得到k-1次多項式函數，銜接處的平滑性是Cᵏ⁻² continuity。也就是說，第k-1次微分的時候，左鄰居導數值、右鄰居導數值可能不相等。從第0次微分到第k-2次微分，左右鄰居導數值皆保證相等。

總而言之，函數點越多，銜接處越平滑。

fractal noise function

Weierstrass function：疊加各種餘弦波，頻率呈倍數，振幅呈指數。

Fourier–Wiener series：疊加各種弦波，頻率呈倍數，振幅為隨機數。

smooth noise function

計算學家運用「內插」，製造平滑雜訊。網路上已有詳細教學文章，請讀者自行參考。

value noise：等距設置隨機數值，內插得到其餘數值。內插是為了製造綿延感。

Perlin noise：等距設置遞迴碎形，內插得到其餘數值。有些規律、又不失隨機；好像有道理、又好像在鬼扯。非常奇葩。

http://mrl.nyu.edu/~perlin/noise/

fBm noise：疊加各種解析度（頻率）的雜訊。解析度是2的各種次方。雜訊可以是上述任意一種。隱含混沌與碎形的概念，更細膩、更自然。

wavelet noise：疊加各種頻率暨振幅的波。類似fBm noise。