傳送秘密

秘密：一件事情，只有我知，外人不知。

如何在眾目睽睽下傳送秘密呢？

這裡提供兩個策略：掩、飾。

第一個策略是遮掩資料、包裝資料，導致外人看不見。比如寄信，我們使用信封，讓外人無法偷看資料。要驗證外人是否偷看資料，可以使用易碎膠帶；要阻止外人偷看資料，可以使用保險箱。

第一個策略在電腦世界行不通。資料在網路線中、空氣中傳送，包裝薄弱。只需接線、接收，有心人皆可直接取得資料。

第二個策略是修飾資料、加工資料，導致外人看不懂。比如行話，我們去到夜店說要冰塊和鹽，只有熟人才能理解話中有話。

第二個策略在電腦世界行得通。資料套用四則運算，就變得完全令人看不懂。套用反運算，就看得懂了。比如說字母從零開始編號，每個字母乘三加三模二十六，然後字串頭尾對調。

想要實行第二個策略，當事人必須先有共識，你知我知、外人不知；否則外人也能看懂你我傳送的秘密了。比如「從零開始編號……頭尾對調」就是共識。又比如我和你當眾說「老地方見」，外人聽了不知道是哪裡，但是你我早知道老地方是哪裡。外人一旦知道老地方是指什麼，外人就知道你我的行蹤了。

也就是說：你我必須先有共同秘密，才能傳送秘密！雞生蛋蛋生雞，總得起個頭。兩種解法：一、你我事先私下見面，約定第一個共同祕密。二、你我當眾揣摩彼此、塑造共識，形成第一個共同秘密。

你我擁有第一個共同秘密之後，即可利用遞推法，傳送更多秘密。比如過幾天我又和你說「上次隔壁那一家，東西也很棒，待會一起去。」你我分享了更多秘密，但是外人仍舊霧裡看花。

一件事情通常有各式各樣的解讀方式，理論上外人永遠無法正確解讀秘密。但是當傳送秘密越來越多，則解讀方式就越來越少。安全起見，三不五時就要更換第一個共同秘密。

A1與A2事先見面。
A1: 我跟你說，當我說「跑」，我們就逃跑。
A2: 好。

B1與B2事先見面。
B1: 我跟你說，當我說「跑」，我們就往前衝。
B2: 好。

後來A1A2B1B2通通上戰場，
C聽到他們說跑，但是不知道他們打算逃跑還是往前衝。

encrypt / decrypt

「加密」是改變資料外觀。「解密」是回復原本外觀。

資料加密之前叫做「明文plaintext」，加密之後叫做「密文ciphertext」。「加密」是明文變密文，「解密」是密文變明文。

            encrypt
thank you! --------> 3Q!
           <--------
            decrypt

                    encrypt
Fibonacci sequence --------> 13-3-2-31-1-1-8-5
                   <--------
                    decrypt

UVa 425 11220 11385

attack（crack）（cryptanalysis）

「攻擊」、「破解」、「密文分析」就是給定密文，找出明文，在不知道加密解密方式的情況下。

[ciphertext]
O, Draconian devil! Oh, lame saint. P.S. Find Robert Langdon.

please find plaintext.

即便外人不知道加密解密方式，外人還是可以用試誤法，窮舉各種加密解密可能性，一一嘗試解密，總有一種會成功。即便密文有很多種解讀方式，外人仍然可以大概猜出個端倪。

UVa 795 828 11697

加密解密基本原理：substitution與transposition

現今的加密演算法，通通都是換字面（substitution）、換位置（transposition）。這是最符合電腦運作特性的方式。

你我事先見面約定換字面、換位置的表格，不讓外人知道；如此一來，只有你我可以加密解密。

設計表格時，要注意密文是否可以正確還原成明文。用數學的術語來說就是：表格必須擁有反函數。

void substitution_encrypt() { char s[10] = "Hello!", t[10] = ""; // 建立轉換表格 char table[128]; for (int i=0; i<128; i++) table[i] = i; table['!'] = 'w'; table['H'] = 'Y'; // 開始轉換 int n; for (n=0; s[n] != '\0'; n++) t[n] = table[ s[n] ]; t[n] = '\0'; } void substitution_decrypt() { // 省略 } void transposition_encrypt() { char s[10] = "Hello!", t[10] = ""; // 建立轉換表格 int table[50]; for (int i=0; i<50; ++i) table[i] = i; table[2] = 3; table[3] = 5; table[5] = 2; // 開始轉換 int n; for (n=0; s[n] != '\0'; n++) t[n] = table[ s[n] ]; t[n] = '\0'; } void transposition_decrypt() { // 省略 }

UVa 306 458 468 554 641 726 850 856 865 10082 10222 10896 11278 11541 11946

攻擊基本原理：frequency analysis與dictionary attack

俗話說：「兵來將擋、水來土掩」。凡有加密解密方式，就有破解方式。

XPUBKPIU ZPKB O QOTUW OTRG JINWT GEJT SERROIN PF
IEZPFW NPXXWTWIK XTER XPUBKPIU ZPKB O FROQQ EIW
PK PF RWTWQG O HJWFKPEI EX PIFKPKJKPIU FPUIF OIN FPUIOQF

換字面的知名破解方式是統計出現頻率（frequency analysis）。首先統計英文對話當中每個英文字母的出現頻率，由高到低依序是etaoinshrdlucmfwypvbgkjqxz。通常密文出現最多次的符號八九不離十就是e！如果e讀起來不通順，那就試t，以此類推。

亦可統計英文對話當中每個英文單字的出現頻率，由高到低依序是the be to of and a in that等等。通常密文多半含有這些單字。

除了針對單一字母、單一單字進行統計，亦得針對雙字母、仨字母、雙單字、仨單字等進行統計，效果更佳。

HET TEGAR SUREAQ SAH ON SCERNOR

換位置的知名破解方式是查字典（dictionary attack）。窮舉字典裡面每一個單字，一一跟密文比對，看看字母數量是否一致、讀起來是否通順。anagram就是這樣的遊戲。

以上提到的攻擊過程都是人工作業。想要寫程式自動作業，那麼讀者必須利用「natural language processing」領域的知識，判斷破解之後的明文是不是可讀的句子、判斷最有可能出現的句子。

其他加密解密的原理

除了換字面、換位置以外，還有很多神奇的加解密原理，不過我沒有仔細研究，大家可以自行研究。

基於符號。換成看不懂的符號。例如火星文、顏文字。事實上我們可以拿編碼演算法、壓縮演算法，當作加密演算法。隨機取一個演算法，稍作修改，不告訴外人，就能利用此演算法加解密。

[ciphertext]
99，3qㄋ姑力i讀豬，偶會+ Uㄉ！

[plaintext]
舅舅，謝謝你鼓勵我讀書，我會加油的！

基於取樣。插入字母拼貼字母。例如《聖經密碼》固定間隔取字母、《火鳳燎原》的城下一聚。

[ciphertext]
Rips ExplAineD thaT eacH codE is a Case Of adDing

[plaintext]
READ THE CODE

基於推理。分析探索已知未知。例如猜數字魔術。例如下面的益智謎題：

X先生、Y先生都具有足夠的推理能力。
這天，他們正在接受推理面試。
他們知道桌子的抽屜裡有如下16張撲克牌:
紅心 A、Q、4
黑桃 J、8、4、2、7、3
梅花 K、Q、5、4、6
方塊 A、5

約翰教授從這16張牌中挑出一張牌來，
並把這張牌的點數告訴X先生，
把這張牌的花色告訴Y先生。

這時，
約翰教授問X先生和Y先生:
你們能從已知的點數或花色中推知這張牌是什麼牌嗎?
X先生:「我不知道這張牌。」
Y先生:「我知道你不知道這張牌。」
X先生:「現在我知道這張牌了。」
Y先生:「我也知道了。」

請問:這張牌是什麼牌?

UVa 10030

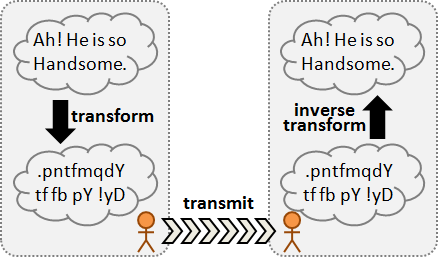
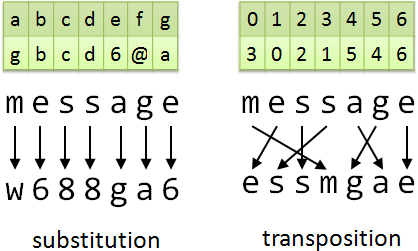
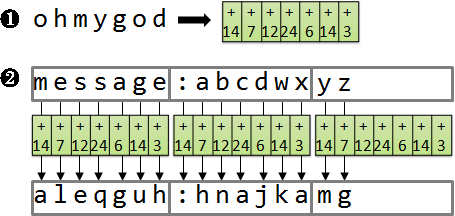
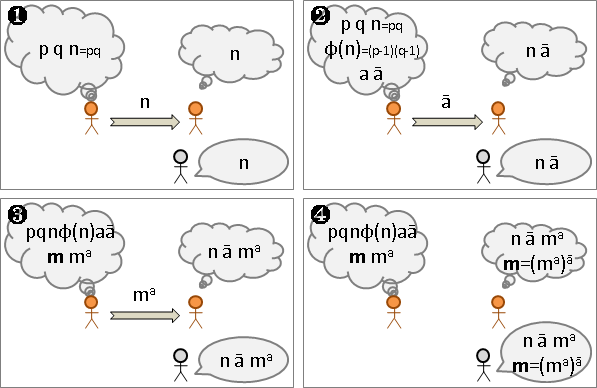
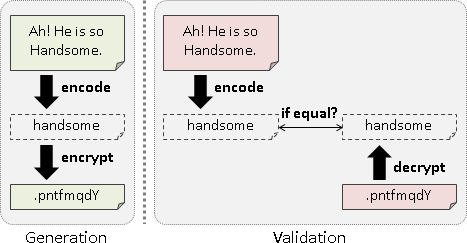
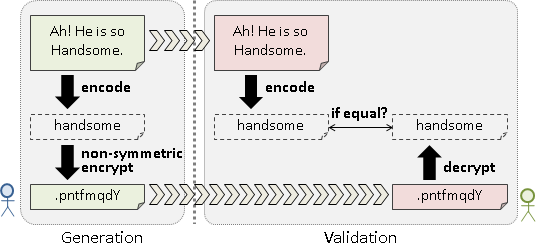
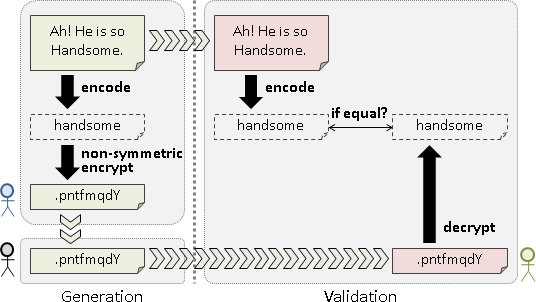
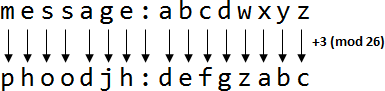Caesar cipher

羅馬帝國時期的演算法。原理是換字面。

加密：明文每個字元加三成為密文。解密：密文每個字元減三成為明文。三是事先約定的秘密，可以改成任意數。

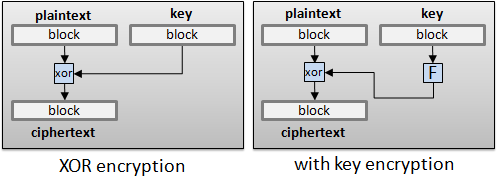
引入密鑰的觀念：事先約定的秘密，只需要一個數字，不需要加密解密方式。加密解密方式可以公諸於世；只要密鑰沒有公諸於世，外人就無法解密。

大小寫、空白鍵、標點符號等細節，請自行制定規則。

string encrypt(string s, int key) { string t; t.resize(s.size()); for (int i=0; i<s.size(); ++i) if (s[i] >= 'a' && s[i] <= 'z') t[i] = (s[i] - 'a' + key) % 26 + 'a'; else t[i] = s[i]; return t; } string decrypt(string t, int key) { string s; s.resize(t.size()); for (int i=0; i<t.size(); ++i) if (t[i] >= 'a' && t[i] <= 'z') s[i] = (t[i] - 'a' - key + 26) % 26 + 'a'; else s[i] = t[i]; return s; }

攻擊方式：頻率分析。甚至可以直接窮舉26種加法量，一一嘗試解密。

ENIGMA

二戰時期的演算法。Caesar cipher的加強版。

引入區塊的觀念：各區塊各自加密解密。事先約定一個短字串當作秘密。

跳著抓字母，就是Caesar cipher。攻擊方式：窮舉各種區塊長度；針對一種區塊長度，跳著抓字母，實施頻率分析。

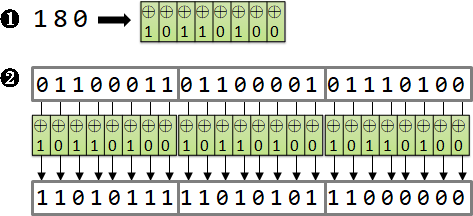
XOR cipher

電腦草創時期的演算法。ENIGMA的加強版。

引入位元的觀念：以位元為基本單元。XOR的意義：位元是否需要改變。事先約定一個二進位整數當作秘密。

偶數次的XOR具有抵消的功效。加密、解密，過程一模一樣！

想要避免頻率攻擊，一種方式是取消區塊。優點：每個位元的改變機率都是1/2，互相獨立，無法分辨明文，形成完美的加密。缺點：事先約定的秘密，必須跟明文一樣長，導致傳輸量遽增。

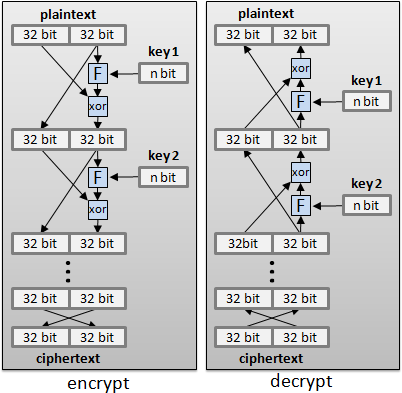
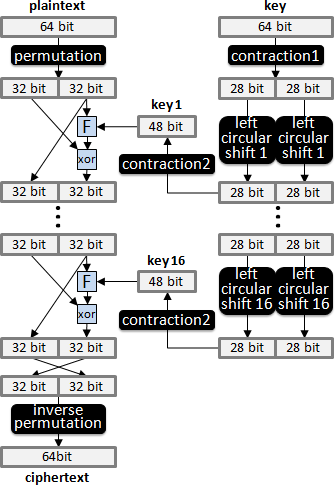
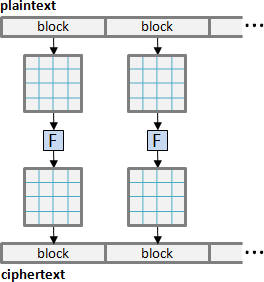
Feistel cipher

XOR cipher的加強版。

事先約定的秘密跟明文一樣長，傳輸量大，無法破解。事先約定的秘密很短，傳輸量小，容易破解。此演算法介於中間。

引入多回合的觀念：盡量讓密文「看起來似乎很亂」。

區塊長度是64 bit。

F是任意的加密演算法，例如換字面、換位置，例如Caesar cipher、ENIGMA。

F也可以是任意的函數，而且F不必擁有反函數！偶數次的XOR具有抵消的功效，因此解密時不必使用F的反函數！

key是事先約定的秘密，自行制定長度；每回合都用不一樣的秘密，以增強加密效果。

最後一回合結束，另外再左右交換一下，打亂文字先後順序。

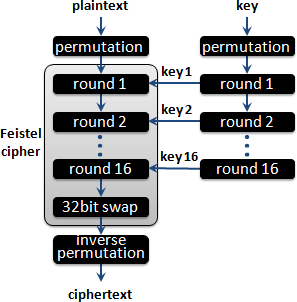
data encryption standard（DES）

Feistel cipher的加強版。已被淘汰，參考看看就好。

引入密鑰調度的觀念：讓每回合的密鑰「看起來似乎很亂」。

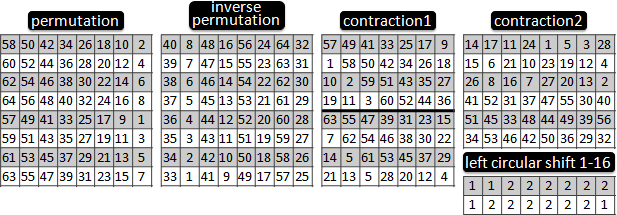
加密的詳細架構如下：

permutation是重新排列換位置。contraction是重新排列並且剔除一些位元。每回合key都被分為兩段，分別往高位數循環位移，位移量只有1和2兩種可能，請查表格；所有回合的位移量總和28，剛好等於位元長度28，剛好繞一圈。

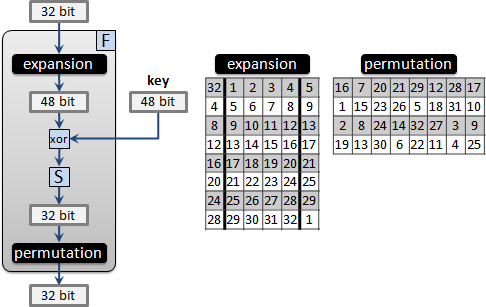
F的構造如下：

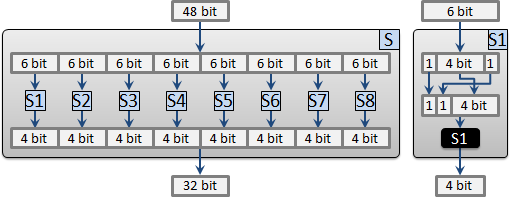
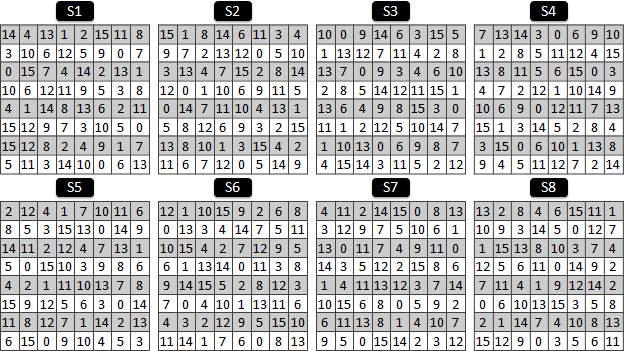
S的構造如下：

附帶一提，每個函數S1到S8的最高位元、最低位元，對應到expansion所拓展的位元。這兩個位元被調整成最高位元。

表格S1到S8是查表：輸入n，輸出表格第n個數。

Hill cipher

經濟大蕭條時期的演算法。

引入線性變換的觀念。加密：套用線性函數（矩陣）。解密：套用反函數（反矩陣）。

advanced encryption standard（AES）
Rijndael cipher

正在使用的演算法。美國國家安全局NSA公開徵選而得。

引入方塊的觀念：區塊排成方塊，方便攪亂順序。

區塊：排成4×4方塊，每格8 bit，總共128 bit。直向排列。

┌───┬───┬───┬───┐
│ 0 │ 4 │ 8 │12 │
├───┼───┼───┼───┤
│ 1 │ 5 │ 9 │13 │   ┌───┐
├───┼───┼───┼───┤   │   │ = 8 bit
│ 2 │ 6 │10 │14 │   └───┘
├───┼───┼───┼───┤
│ 3 │ 7 │11 │15 │
└───┴───┴───┴───┘

四種加密演算法：SubBytes換字面、ShiftRows換位置、MixColumns線性變換、AddRoundKey位元XOR。

加密：四種加密演算法，依序重複N+1回合。第0回合只做AddRoundKey，第N回合不做MixColumns。解密：反過來做。

SubBytes：格子為單位，換字面，請查表格。

                         encrypt
  lsb  0  1  2  3  4  5  6  7  8  9  a  b  c  d  e  f
msb ┌─────────────────────────────────────────────────┐
  0 │ 63 7c 77 7b f2 6b 6f c5 30 01 67 2b fe d7 ab 76 │
  1 │ ca 82 c9 7d fa 59 47 f0 ad d4 a2 af 9c a4 72 c0 │
  2 │ b7 fd 93 26 36 3f f7 cc 34 a5 e5 f1 71 d8 31 15 │
  3 │ 04 c7 23 c3 18 96 05 9a 07 12 80 e2 eb 27 b2 75 │
  4 │ 09 83 2c 1a 1b 6e 5a a0 52 3b d6 b3 29 e3 2f 84 │
  5 │ 53 d1 00 ed 20 fc b1 5b 6a cb be 39 4a 4c 58 cf │
  6 │ d0 ef aa fb 43 4d 33 85 45 f9 02 7f 50 3c 9f a8 │
  7 │ 51 a3 40 8f 92 9d 38 f5 bc b6 da 21 10 ff f3 d2 │
  8 │ cd 0c 13 ec 5f 97 44 17 c4 a7 7e 3d 64 5d 19 73 │
  9 │ 60 81 4f dc 22 2a 90 88 46 ee b8 14 de 5e 0b db │
  a │ e0 32 3a 0a 49 06 24 5c c2 d3 ac 62 91 95 e4 79 │
  b │ e7 c8 37 6d 8d d5 4e a9 6c 56 f4 ea 65 7a ae 08 │
  c │ ba 78 25 2e 1c a6 b4 c6 e8 dd 74 1f 4b bd 8b 8a │
  d │ 70 3e b5 66 48 03 f6 0e 61 35 57 b9 86 c1 1d 9e │
  e │ e1 f8 98 11 69 d9 8e 94 9b 1e 87 e9 ce 55 28 df │
  f │ 8c a1 89 0d bf e6 42 68 41 99 2d 0f b0 54 bb 16 │
    └─────────────────────────────────────────────────┘

                         decrypt
  lsb  0  1  2  3  4  5  6  7  8  9  a  b  c  d  e  f
msb ┌─────────────────────────────────────────────────┐
  0 │ 52 09 6a d5 30 36 a5 38 bf 40 a3 9e 81 f3 d7 fb │
  1 │ 7c e3 39 82 9b 2f ff 87 34 8e 43 44 c4 de e9 cb │
  2 │ 54 7b 94 32 a6 c2 23 3d ee 4c 95 0b 42 fa c3 4e │
  3 │ 08 2e a1 66 28 d9 24 b2 76 5b a2 49 6d 8b d1 25 │
  4 │ 72 f8 f6 64 86 68 98 16 d4 a4 5c cc 5d 65 b6 92 │
  5 │ 6c 70 48 50 fd ed b9 da 5e 15 46 57 a7 8d 9d 84 │
  6 │ 90 d8 ab 00 8c bc d3 0a f7 e4 58 05 b8 b3 45 06 │
  7 │ d0 2c 1e 8f ca 3f 0f 02 c1 af bd 03 01 13 8a 6b │
  8 │ 3a 91 11 41 4f 67 dc ea 97 f2 cf ce f0 b4 e6 73 │
  9 │ 96 ac 74 22 e7 ad 35 85 e2 f9 37 e8 1c 75 df 6e │
  a │ 47 f1 1a 71 1d 29 c5 89 6f b7 62 0e aa 18 be 1b │
  b │ fc 56 3e 4b c6 d2 79 20 9a db c0 fe 78 cd 5a f4 │
  c │ 1f dd a8 33 88 07 c7 31 b1 12 10 59 27 80 ec 5f │
  d │ 60 51 7f a9 19 b5 4a 0d 2d e5 7a 9f 93 c9 9c ef │
  e │ a0 e0 3b 4d ae 2a f5 b0 c8 eb bb 3c 83 53 99 61 │
  f │ 17 2b 04 7e ba 77 d6 26 e1 69 14 63 55 21 0c 7d │
    └─────────────────────────────────────────────────┘

ShiftRows：橫條為單位，左循環移位，位移量漸增。

             ┌───┬───┬───┬───┐     ┌───┬───┬───┬───┐
left shift 0 │ 0 │ 4 │ 8 │12 │     │ 0 │ 4 │ 8 │12 │
             ├───┼───┼───┼───┤     ├───┼───┼───┼───┤
left shift 1 │ 1 │ 5 │ 9 │13 │     │ 5 │ 9 │13 │ 1 │
             ├───┼───┼───┼───┤ ——→ ├───┼───┼───┼───┤
left shift 2 │ 2 │ 6 │10 │14 │     │10 │14 │ 2 │ 6 │
             ├───┼───┼───┼───┤     ├───┼───┼───┼───┤
left shift 3 │ 3 │ 7 │11 │15 │     │15 │ 3 │ 7 │11 │
             └───┴───┴───┴───┘     └───┴───┴───┴───┘

MixColumns：直條為單位，實施固定的線性變換。

┌─           ─┐ ┌───┐   ┌───┐   ┌─           ─┐ ┌───┐   ┌───┐
│ 02 03 01 01 │ │ 0 │   │ 0'│   │ 02 03 01 01 │ │ 4 │   │ 4'│
│             │ ├───┤   ├───┤   │             │ ├───┤   ├───┤
│ 01 02 03 01 │ │ 1 │   │ 1'│   │ 01 02 03 01 │ │ 5 │   │ 5'│
│             │ ├───┤ = ├───┤   │             │ ├───┤ = ├───┤
│ 01 01 02 03 │ │ 2 │   │ 2'│   │ 01 01 02 03 │ │ 6 │   │ 6'│
│             │ ├───┤   ├───┤   │             │ ├───┤   ├───┤
│ 03 01 01 02 │ │ 3 │   │ 3'│   │ 03 01 01 02 │ │ 7 │   │ 7'│
└─           ─┘ └───┘   └───┘   └─           ─┘ └───┘   └───┘
┌─           ─┐ ┌───┐   ┌───┐   ┌─           ─┐ ┌───┐   ┌───┐
│ 02 03 01 01 │ │ 8 │   │ 8'│   │ 02 03 01 01 │ │12 │   │12'│
│             │ ├───┤   ├───┤   │             │ ├───┤   ├───┤
│ 01 02 03 01 │ │ 9 │   │ 9'│   │ 01 02 03 01 │ │13 │   │13'│
│             │ ├───┤ = ├───┤   │             │ ├───┤ = ├───┤
│ 01 01 02 03 │ │10 │   │10'│   │ 01 01 02 03 │ │14 │   │14'│
│             │ ├───┤   ├───┤   │             │ ├───┤   ├───┤
│ 03 01 01 02 │ │11 │   │11'│   │ 03 01 01 02 │ │15 │   │15'│
└─           ─┘ └───┘   └───┘   └─           ─┘ └───┘   └───┘

    encrypt           decrypt
┌─           ─┐   ┌─           ─┐
│ 02 03 01 01 │   │ 0e 0b 0d 09 │
│             │   │             │
│ 01 02 03 01 │   │ 09 0e 0b 0d │
│             │   │             │
│ 01 01 02 03 │   │ 0d 09 0e 0b │
│             │   │             │
│ 03 01 01 02 │   │ 0b 0d 09 0e │
└─           ─┘   └─           ─┘

AddRoundKey：格子為單位，XOR本回合密鑰。

┌───┬───┬───┬───┐   ┌───┬───┬───┬───┐   ┌───┬───┬───┬───┐
│ 0 │ 4 │ 8 │12 │   │k0 │k4 │k8 │k12│   │ 0'│ 4'│ 8'│12'│
├───┼───┼───┼───┤   ├───┼───┼───┼───┤   ├───┼───┼───┼───┤
│ 1 │ 5 │ 9 │13 │   │k1 │k5 │k9 │k13│   │ 1'│ 5'│ 9'│13'│
├───┼───┼───┼───┤ ⊕ ├───┼───┼───┼───┤ = ├───┼───┼───┼───┤
│ 2 │ 6 │10 │14 │   │k2 │k6 │k10│k14│   │ 2'│ 6'│10'│14'│
├───┼───┼───┼───┤   ├───┼───┼───┼───┤   ├───┼───┼───┼───┤
│ 3 │ 7 │11 │15 │   │k3 │k7 │k11│k15│   │ 3'│ 7'│11'│15'│
└───┴───┴───┴───┘   └───┴───┴───┴───┘   └───┴───┴───┴───┘

KeyExpansion：密鑰調度。活用上述四種加密演算法，求得每回合密鑰。細節請見維基百科：

美國國家安全局NSA提供的演算法標準文件：

網路上找到的實作程式碼：

ChaCha cipher

正在使用的演算法。以XOR cipher為基礎，參考Rijndael cipher改良而得。

引入密鑰加密【尚無正式名稱】的觀念：XOR cipher不需修飾明文，只需修飾密鑰。只對密鑰實施加密演算法，以節省計算時間。

區塊：排成4×4方塊，每格32 bit。橫向排列。

┌───┬───┬───┬───┐
│ 0 │ 1 │ 2 │ 3 │
├───┼───┼───┼───┤
│ 4 │ 5 │ 6 │ 7 │   ┌───┐
├───┼───┼───┼───┤   │   │ = 32 bit
│ 8 │ 9 │10 │11 │   └───┘
├───┼───┼───┼───┤
│12 │13 │14 │15 │
└───┴───┴───┴───┘

方塊包含四種數字：常數constant、密鑰key、區塊編號block count、亂數種子nonce。排版請見下圖。

┌───┬───┬───┬───┐
│ c │ c │ c │ c │
├───┼───┼───┼───┤
│ k │ k │ k │ k │
├───┼───┼───┼───┤
│ k │ k │ k │ k │
├───┼───┼───┼───┤
│ b │ n │ n │ n │
└───┴───┴───┴───┘

常數：0x657870616e642033322d62797465206b。

常數是expand 32-byte k的ASCII編碼。想必是作者的提示。

密鑰：256 bit，只佔8格。其餘格子用其他三種數字補足。

區塊編號：從0開始。

亂數種子：事先指定一個隨機數。範例請見下圖。

constant    = (65:78:70:61:6e:64:20:33:32:2d:62:79:74:65:20:6b)
key         = (00:01:02:03:04:05:06:07:08:09:0a:0b:0c:0d:0e:0f:
               10:11:12:13:14:15:16:17:18:19:1a:1b:1c:1d:1e:1f)
block count = 1
nonce       = (00:00:00:09:00:00:00:4a:00:00:00:00)

┌──────────┬──────────┬──────────┬──────────┐
│ 65787061 │ 6e642033 │ 322d6279 │ 7465206b │
├──────────┼──────────┼──────────┼──────────┤
│ 00010203 │ 04050607 │ 08090a0b │ 0c0d0e0f │
├──────────┼──────────┼──────────┼──────────┤
│ 10111213 │ 14151617 │ 18191a1b │ 1c1d1e1f │
├──────────┼──────────┼──────────┼──────────┤
│ 00000001 │ 00000009 │ 0000004a │ 00000000 │
└──────────┴──────────┴──────────┴──────────┘

byte reversal：每個格子，以byte為單位，頭尾顛倒。

65:78:70:61 ---> 61:70:78:65
6e:64:20:33 ---> 33:20:64:6e
     :                :

quarter round：選定四個格子abcd進行加密，融合了線性變換、位元XOR、位元左循環移位（換字面）。換位置太麻煩不做。

a += b; d ^= a; d <<<= 16;
c += d; b ^= c; b <<<= 12;
a += b; d ^= a; d <<<= 8;
c += d; b ^= c; b <<<= 7;

方塊加密流程：一、byte reversal。二、四個直條、四個反斜線，依序進行quarter round。重複10回合。格式請見下圖。三、步驟一和步驟二的結果相加（換字面）。四、byte reversal。

/ a▪▪▪   ▪a▪▪   ▪▪a▪   ▪▪▪a   a▪▪▪   ▪a▪▪   ▪▪a▪   ▪▪▪a \
⎸ b▪▪▪ → ▪b▪▪ → ▪▪b▪ → ▪▪▪b → ▪b▪▪ → ▪▪b▪ → ▪▪▪b → b▪▪▪ ⎹ × 10
⎸ c▪▪▪   ▪c▪▪   ▪▪c▪   ▪▪▪c   ▪▪c▪   ▪▪▪c   c▪▪▪   ▪c▪▪ ⎹
\ d▪▪▪   ▪d▪▪   ▪▪d▪   ▪▪▪d   ▪▪▪d   d▪▪▪   ▪d▪▪   ▪▪d▪ /

加密暨解密：方塊還原成區塊，明文區塊和該區塊做XOR。

網際網路工程任務組IETF提供的演算法標準文件：

演算法作者的實作程式碼：

加密解密基本原理：block cipher mode與key schedule

「區塊加密模式」。利用先前區塊的密文，改良當前區塊的密文。目前已有多種手法，但是缺乏科學根據。詳情請見維基百科：

「密鑰調度」。區塊之間也可以做密鑰調度。利用先前區塊的密鑰，改良當前區塊的密鑰。目前沒有固定手法，大家自由發揮。

最後講個八卦

相傳圖靈帶頭破譯ENIGMA，然而他只是破譯團隊當中的一員、破譯過程當中的一段。類似的神話故事還有愛迪生發明電燈。

cryptographic function

加密是明文變成密文。一個東西變成另一個東西，概念等同於數學術語「函數」。加密可以視作函數，稱作「密碼學函數」。

一種方式：輸入明文，輸出密文。密鑰用來製造函數。

fkey(plaintext) = ciphertext
g(key) = fkey

另一種方式：輸入明文與密鑰，輸出密文。

f(plaintext, key) = ciphertext

什麼是優秀的加密、差勁的加密呢？目前沒有定論！

要避免外人從密文猜出明文，有時候也要避免外人看穿明文如何變成密文。大致能想到的有：

一、明文與密文一一對應。
二、明文與密文隨機對應。（關於隨機，請見本站文件「random number」。）
三、明文與密文相差極大。
四、明文稍微改動，密文劇烈變動。
五、密文稍微改動，明文劇烈變動。

many-to-one function / one-to-one function

f(x) = y，相同的x對應相同的y，有些不同的x對應相同的y，這樣的f稱作「多對一函數」。

f(x) = y，相同的x對應相同的y，不同的x對應不同的y，這樣的f稱作「一對一函數」。

hash function

f(x) = y，自訂y的範圍大小，這樣的f稱作「雜湊函數」。

學過資料結構「hash table」的讀者應該不陌生才對。

如果讓y的範圍小於x的範圍，就會形成多對一函數。一般來說，大家提到雜湊函數，習慣預設y的範圍小於x的範圍。

pseudorandom function / pseudorandom permutation

「偽隨機函數」。x與y的對應，看起來似乎很亂。

「偽隨機排列」。x與y一樣多＆一對一函數＆偽隨機函數。

計算機只能接受明確指令，大家只好使用明確演算法來製造隨機排列。具備明確規律，卻假裝隨機，於是稱之為「偽」。

大家努力讓偽隨機排列「看起來似乎很亂」。但由於缺乏「亂」的明確定義，所以無法精準評比優劣。一切都是靠感覺，很不科學。

換字面、換位置，其實都是偽隨機排列。先前介紹的加密演算法，其實都是偽隨機排列，除了XOR cipher系列。

one-way function

f(x) = y，給x求y算很快，給y求x算很久，這樣的f稱作「單向函數」。

所謂單向函數，是指很難反向，不是指無法反向。凡是離散函數，窮舉法必能反向。

知名範例是整數乘法、整數分解。

f(a,b) = ab
整數乘法：給a和b求ab。時間複雜度是一次整數乘法。
整數分解：給ab求a和b。試除法，時間複雜度是sqrt(ab)次整數除法。

知名範例是餘數次方、餘數開方。

f(a) ≡ aᵏ (mod m)   k m是常數
餘數次方：給a求aᵏ。時間複雜度是log(k)次餘數乘法。
餘數開方：給aᵏ求a。NP-complete。

collision-free function（collision-resistant function）

f(x₁) = f(x₂)，符合條件的x₁與x₂稱作「碰撞」。

f(x₁) = f(x₂)，求得符合條件的x₁與x₂要算很久，這樣的f稱作「無碰撞函數」。

所謂無碰撞函數，是指很難找到碰撞，不是指沒有碰撞。凡是多對一函數，必有碰撞。

cryptographic hash function（cryptographic many-to-one collision-free one-way pseudorandom hash function）

「密碼學雜湊函數」。加密很快，解密很久。

大家的需求，目前是這五樣，以後還可能更多：

雜湊函數的用途：密文限制長度。
隨機函數的用途：密文看起來似乎很亂。
單向函數的用途：難以還原明文。
無碰撞函數的用途：難以偽造明文。
多對一函數的用途：難以確定明文。

不必解密、不被解密，這種情況下適合使用密碼學雜湊函數。例如XOR cipher，解密不需要反函數，可用此函數做密鑰加密。

不必解密、不被解密，因此密碼學雜湊函數不含密鑰。

攻擊基本原理：rainbow table attack

尋找碰撞的知名方式是彩虹表攻擊。

曾經計算過的x與y，一對一對儲存起來，以後直接查表。

攻擊基本原理：brute-force attack與birthday attack

尋找碰撞的知名方式是暴力攻擊和生日攻擊。

暴力攻擊：依序窮舉x。根據鴿籠原理，最差N+1次，必定成功。N是y的數量。

生日攻擊：隨機窮舉x。根據生日問題，經過sqrt(N)次，成功機率可過半。N是y的數量。

簡單起見，假設一年365天，假設每天出生機率均等。

鴿籠原理：366人之中，一定有人生日碰巧相同。

生日問題：K人之中，有人生日碰巧相同的機率如下。

所有可能性　　　　365ᴷ = 365×365×365×...
生日皆異的可能性　P(365,K) = 365×364×363×...
生日相同的可能性　365ᴷ - P(365,K)
生日相同的機率　　(365ᴷ - P(365,K)) / 365ᴷ
N日K人版本　　　　(Nᴷ - P(N,K)) / Nᴷ

想讓機率過半，固定N的情況下，那麼K要足夠大，K ≈ sqrt(N)。推導過程請見：

延伸閱讀：pseudorandom generator theorem

有人利用機率學的均勻分布，重新定義隨機函數、單向函數。

並且發現以下性質：一、隨機數能產生隨機函數，隨機函數能產生隨機排列。反之亦然。二、隨機函數能產生單向函數。反之亦然。

但是注意到，「均勻分布」只是「隨機」的需求之一，「隨機」只是「加密」的需求之一，而「隨機」和「加密」的需求至今仍然沒有明確規範。因此，實務上沒人利用這些性質建立加密演算法。

此處不介紹這些性質。有興趣的讀者請自行查閱維基百科：

MD5

容易找到碰撞，已被淘汰。

SHA-2

正在使用的演算法。美國國家安全局NSA自行開發而得。

SHA-3

尚未使用的演算法。美國國家標準技術局NIST公開徵選而得。

BLAKE3

加密解密基本原理：one-way compression function

「單向壓縮函數」。利用先前區塊的雜湊值，改良整體的雜湊值。目前已有多種手法，但是缺乏科學根據。詳情請見維基百科：

「單向壓縮函數」的地位宛如先前章節的「區塊加密模式」。雖然名稱有壓縮二字，但是其實毫無關聯。命名品味不太好。

Diffie–Hellman key exchange

本單元的先備知識是「residue」！

想要傳送秘密，你我必須事先私下見面約定共同秘密。然而在電腦世界當中，你我無法事先私下見面。因此有人想出在公開場合建立共同秘密的演算法。由於非常簡單易用，似乎沒人再去設計其他演算法了。

g^(a×b) ≡ (g^a)^b ≡ (g^b)^a (mod p)

一、甲乙公開協議一個質數p。p作為模數。
　　甲乙公開協議一個數字g。
二、甲心中隨便想一個數字a。
　　乙心中隨便想一個數字b。
三、甲計算g^a，傳送給乙，乙獲得g^a。
　　乙計算g^b，傳送給甲，甲獲得g^b。
四、甲計算(g^b)^a，乙計算(g^a)^b，
　　兩人求得共同秘密(g^a)^b。

外人只知道g、g^a、g^b、p，外人無法快速計算(g^a)^b。
想破解，必須求得a，必須計算log(g^a)求得a。（或者是b）
然而log得花很多時間！

遺珠之憾是不能控制共同秘密為何。

當數字很小，餘數次方的時間複雜度是O(log(n))，建立速度極快；餘數對數的時間複雜度是O(sqrt(n))，破解速度也算快。

當數字夠大，餘數對數演算法的記憶體便不敷使用，必須改用試誤法，時間大幅成長為O(n)！利用餘數次方與餘數對數的時間差，讓外人一時無法破解；當外人破解時，秘密早就傳送完畢了！

然而外人只要肯花時間，總有一天還是能破解秘密。實務上的應對方式是資料分段加密、資料分流傳送，讓外人永遠無法追上最新進度，讓外人無法獲得資料全貌。

餘數系統改成finite field、改成elliptic curve

此處的餘數系統，基本單元是整數。我們可以進一步把整數改成餘數多項式、改成橢圓曲線格點，讓對數更難計算、計算更久。

最後講個八卦

演算法作者其實不是這兩人。原作者創造許多傳送秘密的重要觀念，然而太過突發奇想、太過簡潔單純，不被指導教授接受。原作者只好跨校找Hellman協助完成論文、完成學業。後來此演算法變成網路傳輸的重要關鍵，這兩人藉勢得了圖靈獎。

以Diffie–Hellman key exchange得到的共同秘密來加密解密
【目前稱作symmetric-key encryption】

用來加密解密的共同秘密，英文稱作key，中文譯作「金鑰」或「密鑰」。共同秘密宛如鑰匙，開啟得到明文、關閉得到密文。

壹、Diffie–Hellman key exchange：
　一、甲乙公開協議一個質數p。p作為模數。
　　　甲乙公開協議一個數字g。
　二、甲心中隨便想一個數字a。
　　　乙心中隨便想一個數字b。
　三、甲計算g^a，傳送給乙，乙獲得g^a。
　　　乙計算g^b，傳送給甲，甲獲得g^b。
　四、甲計算(g^b)^a，求得共同秘密(g^a)^b = s。
　　　乙計算(g^a)^b，求得共同秘密(g^a)^b = s。
貳、任意一個加密演算法：
　一、甲利用s加密。
　二、乙利用s解密。

接收端口【目前稱作public-key encryption】

調整步驟順序，引入接收端口的觀念。

壹、乙建立接收端口：
　一、甲乙公開協議一個質數p。p作為模數。 （乙公佈一個質數p）
　　　甲乙公開協議一個數字g。　　　　　　（乙公佈一個數字g）
　二、乙心中隨便想一個數字b。　　　　　　（乙心中隨便想一個數字b）
　　　乙計算g^b，傳送給甲，甲獲得g^b。　 （乙公佈g^b）
貳、甲加密：
　一、甲心中隨便想一個數字a。
　　　甲計算g^a，傳送給乙，乙獲得g^a。
　二、甲計算(g^b)^a，求得共同秘密(g^b)^a = s。
　三、甲利用s加密。
參、乙解密：
　一、乙計算(g^a)^b，求得共同秘密(g^a)^b = s。
　二、乙利用s解密。

隱藏數字a，英文稱作private key，中文譯作「私鑰」。公開數字g^b，英文稱作public Key，中文譯作「公鑰」。

甲每次加密都可以重新想一個數字a，密文更不容易破解；乙每次解密都可以用同一個數字g^b，密文更容易接收。

人人都知道g^b，人人都可以利用g^b傳送秘密給乙，人人都無法窺伺彼此秘密！

機制類似聯絡地址、聯絡電話。乙提供服務專線0800-092-000，人人皆可撥打專線聯絡乙，人人皆無法獲知其他人的電話內容！

此演算法的特色：人人都能加密，只有乙能解密！

發送端口【目前稱作digital signature】

追加單向函數，引入發送端口的觀念。

甲傳送密文給大家，並且公布解密方式，讓大家都可以解密。資料沒有任何保密效果，但是大家可以確信資料來自同一人。

機制類似產品商標。甲請大家認明三支雨傘標，人人都可以進行檢視，確信產品來自同一人！

此演算法的特色：只有甲能加密，人人都能解密！

傳送秘密現在有了三種模式：一到一、多到一、一到多。

餘數加法

餘數加法有著換字面的功效。對象是小寫英文字母，模數設定成26。對象是位元組，模數設定成2⁸ = 256。

餘數加法、餘數減法（餘數加法反運算），一加一減相互抵銷。我們可以以此設計一個超級簡單的加密演算法：

加密：明文加s成為密文。解密：密文減s成為明文。s是事先約定的秘密。

Caesar cipher

餘數加法。報告完畢。

餘數乘法

餘數乘法有著換字面的功效。乘法是加法來的。

餘數乘法、餘數除法（餘數乘法反運算），一乘一除相互抵銷。我們可以以此設計一個超級簡單的加密演算法：

加密：明文乘以s成為密文。解密：密文乘以s的倒數成為明文。s是事先約定的秘密。

模數必須是質數，才有乘法反運算，才能解密。餘數系統改成finite field、改成elliptic curve，模數就有更多選擇。

ElGamal encryption

餘數乘法。接收端口。

餘數次方

餘數次方有著換字面的功效。次方是乘法來的。

餘數次方、餘數開方（餘數次方反運算），次方開方相互抵消。我們可以以此設計一個超級簡單的加密演算法：

加密：明文的s次方成為密文。解密：密文的s倒數次方成為明文。s是事先約定的秘密。

明文必須是原根，才有次方反運算，才能解密。餘數系統改成finite field、改成elliptic curve，明文就不受限制。

注意到次方值的模數是φ(n)，次方值的倒數要用φ(n)來算。

注意到m是明文、n是模數。符號使用方式與數論領域不同。

餘數乘法加密解密：(m×s)×s ≡ m (mod n)     where s×s ≡ 1 (mod n)
餘數次方加密解密：(m^s)^s ≡ m (mod n)     where s×s ≡ 1 (mod φ(n))

RSA encryption

餘數次方。接收端口。

壹、乙建立接收端口：
　一、乙公佈一個質數p。p作為模數。
　　　乙公佈一個數字g。
　二、乙心中隨便想一個數字b。
　　　乙公佈g^b。
貳、甲加密：
　一、甲心中隨便想一個數字a。
　　　甲計算g^a，傳送給乙，乙獲得g^a。
　二、甲計算(g^b)^a，求得共同秘密(g^a)^b = s。
　三、甲有明文m，甲計算m^s，傳送給乙，乙獲得m^s。
參、乙解密：
　一、乙計算(g^a)^b，求得共同秘密(g^a)^b = s。
　二、乙有密文m^s。
　　　乙計算次方的模數φ(p) = p-1。
　　　乙計算s的倒數s，模數是φ(p)。
　　　乙計算(m^s)^s，乙求得明文m。

儘管可以運作，但是一堆次方，看了就煩，乾脆簡化。

壹、乙建立接收端口：
　　乙公佈一個質數p。p作為模數。
　　乙公佈一個數字a。a作為公鑰。
貳、甲加密：
　　甲有明文m。甲計算m^a，傳送給乙，乙獲得m^a。
參、乙解密：
　　乙有密文m^a。
　　乙計算次方的模數φ(p) = p-1。
　　乙計算a的倒數a，模數是φ(p)。
　　乙計算(m^a)^a，乙求得明文m。

再把計算倒數的步驟往前挪，預先計算，不必每次重算。

壹、乙建立接收端口：
　　乙公佈一個質數p。p作為模數。
　　乙公佈一個數字a。a作為公鑰。
　　乙計算a的倒數a，模數是φ(p) = p-1。
貳、甲加密：
　　甲有明文m。甲計算m^a，傳送給乙，乙獲得m^a。
參、乙解密：
　　乙有密文m^a。乙計算(m^a)^a，乙求得明文m。

然而外人知道p、a、m^a，
可以計算φ(p) = p-1，
然後計算a，
然後計算(m^a)^a，求得明文m。

為了不讓外人輕鬆計算a的倒數，把模數從一個質數改成兩個質數相乘，而且不讓外人知道是哪兩個質數。

壹、乙建立接收端口：
　一、乙心中隨便想兩個質數p與q。
　　　乙計算p×q = n。
　　　乙公佈一個數字n。n作為模數。
　二、乙心中隨便想一個數字a。
　　　乙計算a的倒數a，模數是φ(n) = φ(p×q) = (p-1)×(q-1)。
　　　乙公佈一個數字a。a作為公鑰。（a亦可）
貳、甲加密：
　　甲有明文m。甲計算m^a，傳送給乙。
參、乙解密：
　　乙有密文m^a。乙計算(m^a)^a，乙求得明文m。

外人只知道n、a、m^a，外人無法快速計算(m^a)^a。
一、想破解，必須得到m，必須計算ᵃ√m^a得到m。
　　然而開a次方得花很多時間！
二、想破解，另一種方式是求得a。
　　必須計算a的倒數才能求得a，所以必須求得模數φ(n)。
　　必須計算(p-1)×(q-1)才能求得φ(n)，所以必須求得p與q。
　　必須計算n是哪兩個數相乘才能求得p與q。
　　然而質因數分解得花很多時間！

餘數倒數、餘數次方，遠小於餘數開方、整數分解的時間複雜度。原理如同Diffie–Hellman key exchange，利用時間差，讓外人一時無法破解。

ICPC 4353

RSA signature

餘數次方。發送端口。

壹、甲建立發送端口：
　一、甲心中隨便想兩個質數p與q。
　　　甲計算p×q = n，n作為模數。
　　　甲公佈一個數字n。n作為模數。
　二、甲心中隨便想一個數字a。
　　　甲計算a的倒數a，模數是φ(n) = φ(p×q) = (p-1)×(q-1)。
　　　甲公佈一個數字a。a作為公鑰。
貳、甲加密：
　　甲有明文m。甲計算m^a，傳送給乙，乙獲得m^a。
參、乙解密：
　　乙有密文m^a。乙計算(m^a)^a，乙求得明文m。

最後講個八卦

這三位作者跑去申請專利，開了一間公司叫做RSA security。然後美國政府將演算法實作列為軍事管制商品，禁止出口，詳情請見crypto wars與pretty good privacy。然後美國政府兜售自製晶片、埋入監聽系統，該公司登高一呼、挺身對抗，詳情請見clipper chip。然後三位作者藉勢得了圖靈獎。然後媒體爆料該公司被美國政府買通，使用美國政府設計的、藏有後門的演算法，讓美國政府可以破解秘密、監聽訊息，詳情請見RSA backdoor。然後其中一位作者被美國政府拒發入境簽證，理由不明。貴圈真亂。

man-in-the-middle attack

「中間人攻擊」。傳送秘密時，他人佯裝接收對象。得進一步推廣為雙向版本，他人兩面討好、居中斡旋。

勞保黃牛、信用卡客服詐騙、社交工程等等都是中間人攻擊。

中間人攻擊的精髓：接洽對象全是壞人。假的檢察官、假的行員、假的電話號碼、假的法規。極端案例是《楚門的世界》。

中間人攻擊是必勝攻擊手法，所有的加密演算法一律失效！

一種破解方式是確認對象身分。不幸的是，電腦世界當中，訊息在網路上傳輸，可以隨時攔截；而且無法見到對方。

一種破解方式是測量溝通時間。不幸的是，電腦世界當中，訊息在電腦中處理，計算速度飛快，難以察覺差異。

最後大家只好依賴「認證」。

certification

「認證」。傳送秘密前，預先諮詢他人，確認接收對象的身分；或者請對方出具他人頒發的良民證。得進一步推廣為雙向版本，他人列席旁聽、居中調解。

見證人、身分證、印鑑證明、合格標章等等都是認證。

認證的精髓：接洽對象全是好人。由第三方公正人士親自驗明正身，頒發證書，昭告天下。極端案例是「好人好事代表」。

「中間人攻擊」和「認證」皆運用了第三者的概念，本質相同、卻又相對，正所謂陰陽相生相剋。第三者可以為善、可以為惡。

confidentiality

一份資料，只給自己人知道，不給外人知道。

如何確認是自己人？

password

「通行碼」。中文習慣稱作「密碼」，翻譯不太準確。

通行碼的機制很簡單。雙方事先約定關鍵字，一方說出關鍵字，另一方驗證關鍵字。例如《阿里巴巴和四十大盜》的芝麻開門、《魔戒》《指环王》的mellon。

通行碼通常不需要加密。大家習慣背記抄寫明文、而非密文。

通行碼通常需要保密。主要是為了避免他人冒用身分為非作歹。也可以不保密，與他人分享。

password保密版本

事先做最好的準備、最壞的打算。使用者必須防止外人得知通行碼，管理者必須預設外人入侵伺服器、盜取通行碼。

一、設計通行碼。讓通行碼毫無規律、難以聯想。例如不要使用生日。甚至以亂數演算法決定通行碼。令外人難以猜中。

二、傳送通行碼。使用者加密通行碼，傳送密文，管理者解密通行碼。令外人無法窺視。

三、保存通行碼。管理者加密通行碼，儲存密文。只有管理者知道密鑰。即便外人盜取通行碼密文，也不知道如何解密。

四、驗證通行碼。甲、收到的通行碼實施加密、伺服器的通行碼密文，比對兩者；乙、收到的通行碼、伺服器的通行碼密文實施解密，比對兩者。大家傾向採用甲，只需加密，不需解密。令外人無法盜取解密程式、無法解密通行碼密文。

保護通行碼：cryptographic hash function

管理者儲存通行碼密文，理應使用一對一函數，然而大家習慣採用多對一函數。

一對一函數，不同的通行碼，對應不同的通行碼密文。優點是避免外人亂敲亂打通行碼，碰巧通行碼密文一樣，導致驗證通過。

多對一函數，有些不同的通行碼，碰巧通行碼密文一樣。優點是即使外人竊取通行碼密文，也無法從反向推導通行碼，可能性太多。

製作通行碼密文的密碼學雜湊函數有bcrypt、PBKDF2、scrypt、Argon2。

authentication

一份資料，作者身分為真，未經他人冒名頂替。

如何確認資料是否為他人偽作？

signature

「簽名」。創立獨門絕技，只有本人能達成，避免冒名頂替。

integrity

一份資料，資料內容為真，未經他人竄改造假。

如何確認資料未經竄改？

digest

「摘要」。增加檢查項目，確認是否相符，避免竄改造假。

大家把簽名與摘要混為一談，使用相同的演算法。

digest私藏版本

首先利用編碼演算法製作摘要！

避免他人只竄改本文、只竄改摘要：相同本文得到相同摘要，不同本文得到不同摘要；從本文到摘要是一對一函數。

壹、製作摘要：
　一、甲心中隨便想一個編碼演算法。
　二、甲編碼本文，得到摘要。
貳、檢查摘要：
　一、甲編碼本文，得到新摘要。
　二、甲比對舊摘要、新摘要。
　　　若一致，本文未竄改。
　　　若不一致，本文已竄改。

接著利用加密演算法掩飾摘要！

避免他人同時竄改本文和摘要：加密本文、或者加密摘要、或者兩者皆加密。一般僅加密摘要，節省時間。

壹、製作摘要：
　一、甲心中隨便想一個編碼演算法。
　二、甲編碼本文，得到摘要。
　三、甲心中隨便想一個加密演算法。（以及密鑰）
　四、甲加密摘要，得到摘要密文。
貳、檢查摘要：
　一、甲編碼本文，得到新摘要。
　二、甲加密新摘要，得到新摘要密文。
　三、甲比對舊摘要密文、新摘要密文。
　　　若一致，本文未竄改。
　　　若不一致，本文已竄改。

第二三步可以改成：甲解密舊摘要密文，然後改為比對舊摘要、新摘要。

此方式僅適用單人。一旦他人知道密鑰，那麼他人就可以解密、竄改、重新加密，令偽本文、偽摘要兩相符合。

digest公開版本

繼續利用非對稱式加密來製作摘要！

避免他人只竄改本文、只竄改摘要：只允許本人製作摘要！如此一來，他人擅自改動本文，也無法重製摘要；他人擅自改動摘要，也無法與本文的編碼結果相符。

一種實踐方式是非對稱式加密：只有本人知道如何加密，他人不知道如何加密。

壹、製作摘要：
　一、甲公佈一個編碼演算法。
　二、甲編碼本文，得到摘要。
　三、甲公佈一個非對稱式加密演算法。（只有甲知道如何加密，他人不知。）
　四、甲加密摘要，得到摘要密文。
　五、本文、摘要密文一併傳送給他人。
貳、檢查摘要：
　一、他人編碼本文，得到摘要。
　二、他人解密摘要密文，得到摘要。
　三、他人比對兩份摘要。
　　　若一致，本文未竄改。
　　　若不一致，本文已竄改。

避免他人同時竄改本文和摘要：找公證人登記摘要密文，先登記先贏。再由公證人宣布解密方式。

壹、製作摘要：
　一、甲公佈一個編碼演算法。
　二、甲編碼本文，得到摘要。
　三、甲心想一個非對稱式加密演算法。（只有甲知道如何加密，他人不知。）
　四、甲加密摘要，得到摘要密文。
　五、甲洽詢公證人，登記㊣摘要密文、㊣解密方式。
　六、本文、摘要密文一併傳送給他人。
貳、檢查摘要：
　一、他人編碼本文，得到摘要。
　二、他人洽詢公證人，搜尋摘要密文，得到㊣解密方式。
　三、他人解密摘要密文，得到摘要。
　四、他人比對兩份摘要。
　　　若一致，本文未竄改。
　　　若不一致，本文已竄改。

不幸的是，如果公證人變成海邊的消波塊、山上的堆肥桶，就無法確認本文是否被竄改了。

因而又衍生許多攻防技術，例如台灣的白色恐怖時期、《進撃の巨人》的雷斯家族、《ONE PIECE》的歷史本文。這已經超出加密演算法的範圍，就此打住。

縮短摘要長度：cryptographic hash function

縮短摘要長度，可以節省時間與空間！

製作摘要理應使用一對一函數。摘要盡量短，又滿足一對一函數，其極限是壓縮演算法！如果摘要更短，便無法滿足一對一函數，而形成多對一函數。有失有得。

衍生的副作用：一、不同的明文得到一樣的密文；二、外人難以從密文猜中原文。

製作摘要的演算法有ECDSA、EdDSA。

password vs. signature

通行碼、簽名，兩者都是驗證身分的機制。

通行碼，多傳一，對稱式加密。

簽名，一傳多，非對稱式加密。

兩者都使用了密碼學雜湊函數，製造通行碼密文、縮短簽名。