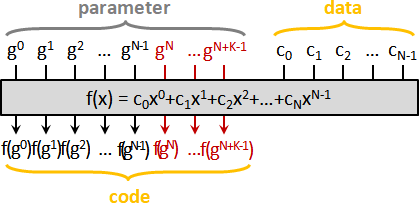
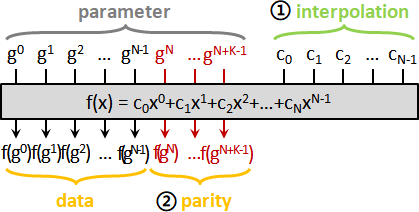
Error Detection

「錯誤偵測」。判斷資料是否損毀變異。

Channel

天有不測風雲，人有旦夕禍福。

電腦世界當中，資料通常是經過傳輸而損毀。於是數學家想像有一個「通道」，宛如函數，一筆資料經過通道得到一筆資料，可能不變，可能出錯。

數學家引入機率的概念、引入遞增法化整為零的概念，令每一個位元有固定機率出錯。現實生活有著千奇百怪的出錯原因；數學家便設計了各式各樣的通道，儘量符合現實情況。

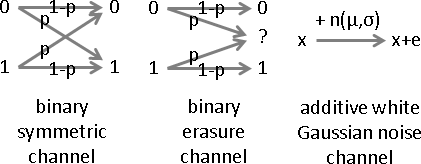
以下文章不談通道，讓事情單純一點！

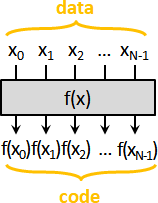
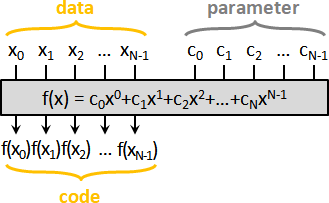
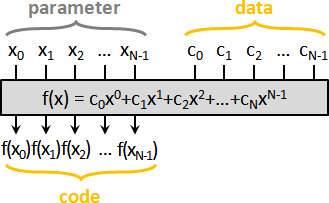
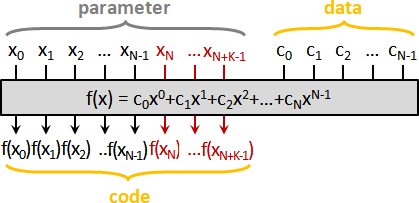
Encode / Decode

不像壓縮和加密特別訂立新名詞，偵測和更正直接沿用舊名詞。

「編碼」是資料變碼。「解碼」是碼變資料。碼經過「通道」將有一定機率損毀變異。

「編碼」是補強資料。「解碼」是復原資料。

         encode
0010001 -------> 001000100100010010001
                           ↓ channel
0010001 <------- 001100110100010010000
         decode
    (detect/correct)

以指數指標偵測錯誤

設立指數指標，判斷指數指標是否一致。

資料：時今
筆劃：14

資料：時令
筆劃數量不同，發現錯誤。

Checksum

以雜湊值偵測錯誤。

編碼：資料代入雜湊函數，得到雜湊值，添在資料尾端。

偵測：資料代入雜湊函數，得到雜湊值，檢查是否相符。

仿照字串搜尋「Karp–Rabin Algorithm」。

Luhn Algorithm

Hill Code

雜湊函數是一次函數。

資料長度n。挑選n個權重，形成1個加權平均數。挑選m組權重，形成m個加權平均數，併成雜湊值。雜湊值長度m。

一種方便的設置：挑選一組權重a₁ a₂ ... aₙ。權重分別1次方、2次方、...、m次方，得到m組權重。

一種方便的設置：建立大矩陣，從中挑選一個m×n子矩陣。

仿照「Hill Cipher」。

Damm Algorithm

以餘數偵測錯誤

資料視作被除數，自行挑選除數，求得餘數，添在資料尾端。

Parity Check：除數是2。
Cyclic Redundancy Check：除數是自訂數字。

Parity Check

奇偶檢查。計算資料有幾個位元1。資料尾端添上一個位元，偶數添0、奇數添1，使得碼有偶數個位元1。

編碼：資料所有位元XOR（求和、模2），得到一個位元（稱作parity），添在資料尾端。

00110001 ---> 001100011
0+0+1+1+0+0+0+1 ≡ 1 (mod 2)

10101001 ---> 101010010
1+0+1+0+1+0+0+1 ≡ 0 (mod 2)

偵測：碼所有位元XOR，等於0則對，等於1則錯。

001100011
0+0+1+1+0+0+0+1+1 ≡ 0 (mod 2) ✔

101011010
1+0+1+0+1+1+0+1+0 ≡ 1 (mod 2) ✖

錯零個位元、錯一個位元，保證正確偵測錯誤。錯兩個位元以上，不保證正確偵測錯誤。

UVa 541

Cyclic Redundancy Check（CRC）

資料視作餘數多項式。係數模2。

11100010 ←—→ x⁷ + x⁶ + x⁵ + x (mod 2)

事先約定一個除數。

11000101 ←—→ x⁷ + x⁶ + x² + 1 (mod 2)

編碼：資料尾端補零（向左移位），數量是除數長度減一，以便置放餘數。

11100010 ---> 111000100010111
111000100000000 ÷ 11000101 ≡ 10111011 ... 0010111 (mod 2)

偵測：整除即正確，不整除即錯誤。

111000100010111 ÷ 11000101 ≡ 0 (mod 2) ✔

錯誤位元數量，少於除數長度，則保證正確偵測錯誤。

UVa 128

Erasure Correction

「抹消更正」。已知損毀變異的地方，嘗試修復資料。

以指數指標修復錯誤

我不確定是否有這種東西。

關鍵字可能是Homomorphic Hashing。

以餘數修復錯誤

看看損毀變異的地方，應該改成多少數字，才能整除。

Parity Check

更正：碼所有正確位元XOR，得到一個位元，作為損毀位元。

00110001 ---> 10110001
0+1+1+0+0+0+1 ≡ 1 (mod 2) 

10101001 ---> 10101001
1+0+1+0+1+0+1 ≡ 0 (mod 2)

損毀位元數量，少於2個，則保證正確修復錯誤。

Cyclic Redundancy Check（CRC）

更正：化作一次方程組求解。

損毀位元數量，少於除數長度，則保證正確修復錯誤。

Fountain Code

Luby Transform Code

Tornado Code

Raptor Code

以多項式內插修復錯誤

函數。N個輸入，作為資料。N個輸出，作為碼。

多項式函數。N個輸入，作為資料。N個輸出，作為碼。

多項式函數。N個係數，作為資料。N個輸出，作為碼。

編碼：多項式求值。指定N個輸入，計算N個輸出。

解碼：多項式內插。N個輸入、N個輸出，計算N個係數。

追加K個輸入，用來容錯。計算N+K個輸出，作為碼。

解碼：尚未損毀變異的地方，挑出N個輸出，輔以N個輸入，實施多項式內插，得到N個係數，成功還原資料。

錯誤數量小於等於K個，則保證正確修復錯誤。

Unisolvence Theorem

多項式函數：考慮N-1次多項式，總共N個係數。

唯一解定理：隨意選定N個輸入（不可重複）。N個係數、N個輸出，形成一對一轉換！

詳情請見本站文件「Polynomial Interpolation」。

Finite Field

實數改成有限體，唯一解定理依然成立。【尚待確認】

電腦採用二進位，有限體適合採用GF(2ⁿ)。

如此一來，係數、輸入、輸出，都是二元碼了。

詳情請見本站文件「Finite Field」。

Generator

輸入設定成原元素g的各種次方：g⁰ g¹ g² ... gᴺ⁺ᴷ⁻¹。

如此一來，只需事先約定一個數字g，就能求得N+K個輸入，同時確保輸入不重複。

如此一來，編碼就是傅立葉轉換了。

詳情請見本站文件「Fourier Transform」。

Reed–Solomon Code原始版本

資料視作係數。事先約定N+K個輸入，代入多項式，求得N+K個輸出，作為碼。

缺點是資料產生變換。無人使用此方法。

Reed–Solomon Code現行版本

資料視作輸出。事先約定N+K個輸入。前N個用來求得內插多項式；後K個用來求得K個輸出，作為parity。