approximation
approximation
「近似」就是找一個柔順的函數,盡量符合手邊的函數。此函數稱作「近似函數」。
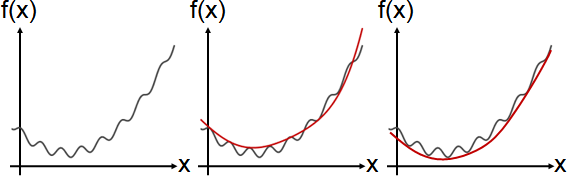
簡易方式:擷取適量的函數點,求得內插函數,作為近似函數。
重大缺點:雖然函數點完全符合,但是其餘部分不保證符合。
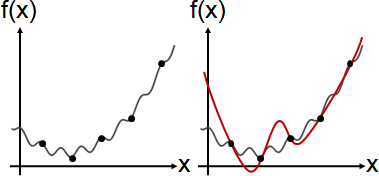
以下介紹保證足夠符合的演算法。
approximation
approximation
「近似」就是找一個柔順的函數,盡量符合手邊的函數。此函數稱作「近似函數」。

簡易方式:擷取適量的函數點,求得內插函數,作為近似函數。
重大缺點:雖然函數點完全符合,但是其餘部分不保證符合。

以下介紹保證足夠符合的演算法。
Weierstrass approximation
先備知識
「binomial expansion」:二項式展開。(x+y)ⁿ展開。
「binomial series」:二項式級數。(x+1)ⁿ展開。
不知道也沒關係。可以暫且跳過。
binomial expansion of 1
1刻意二項式展開。
1 = 1ᴺ = ((1-x) + x)ᴺ = C(N,0)(1-x)⁰xᴺ + C(N,1)(1-x)¹xᴺ⁻¹ + ... + C(N,N)(1-x)ᴺx⁰
按照本站風格重寫數學式子。N是項數,N-1是次方數。
1 = 1ᴺ⁻¹ = ((1-x) + x)ᴺ⁻¹ = C(N-1,0)(1-x)⁰xᴺ⁻¹ + C(N-1,1)(1-x)¹xᴺ⁻² + ... + C(N-1,N)(1-x)ᴺ⁻¹x⁰
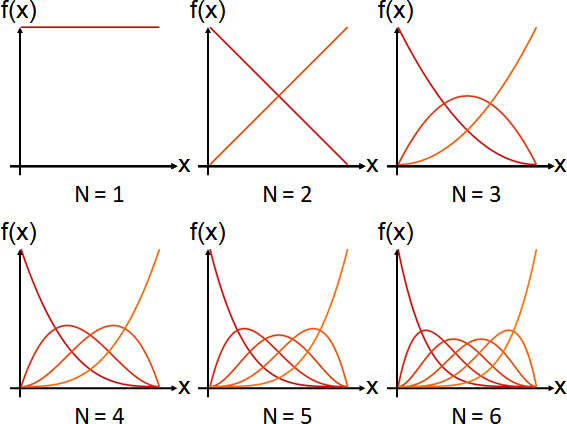
Bernstein polynomial
每一項各是一個Bernstein polynomial。
C(N-1,0)(1-x)⁰xᴺ⁻¹
C(N-1,1)(1-x)¹xᴺ⁻²
:
C(N-1,N)(1-x)ᴺ⁻¹x⁰
Weierstrass approximation
近似函數是N個多項式的加權總和。
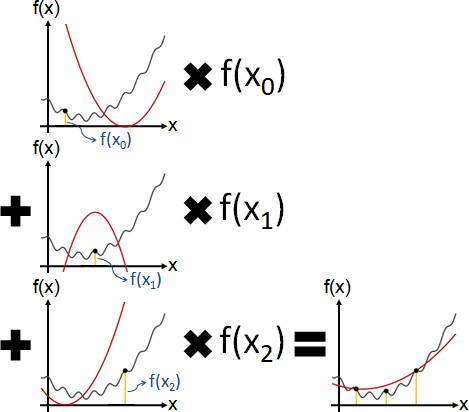
多項式是Bernstein polynomial C(N-1,n) (1-t)ⁿ tᴺ⁻¹⁻ⁿ,權重是函數值f(xₙ),索引值n從0到N-1。
擷取N個位置x₀ ... xɴ₋₁。位置必須等距遞增,依序對應每個多項式。多項式必須縮放平移,[0,1]縮放平移至[x₀,xɴ₋₁]。
多項式縮放平移,想像成原本函數反向縮放平移。大家習慣代入t = (x-x₀) / (xɴ₋₁-x₀)至多項式。t的意義是比例:x₀是t = 0、x₁是t = 1/(N-1)、x₂是t = 2/(N-1)、……、xɴ₋₁是t = 1。
「Weierstrass approximation theorem」:N越大,越符合!
Weierstrass approximation vs. basis interpolation
Weierstrass approximation類似於「basis interpolation」,但是不必穿過所有函數點,也不必解方程組以求得權重,而是直接取函數值作為權重。
Bézier curve
「Bézier curve」使用了Weierstrass approximation。
B-spline approximation
B-spline approximation
Weierstrass approximation進行微調。
優點:函數點不必等距。
原理類似於「B-spline interpolation」,但是不必解方程組以求得權重,而是直接取函數值作為權重。
B-spline curve
「B-spline curve」使用了B-spline approximation。
Taylor approximation
先備知識
「Taylor expansion」:泰勒展開。多項式更換底數。
「Taylor series」:泰勒級數。泰勒展開用於任意函數。
不知道也沒關係。可以暫且跳過。
Taylor series另一種形式
泰勒級數可以改寫成二項式(x-k)ⁿ的加權總和。
k是任意數,例如0。但是注意到f(k) f′(k) f″(x) ...必須存在,而且不能是正負無限大。
f(k) f′(k) f″(k)
f(x) = ————— (x-k)⁰ + ————— (x-k)¹ + ————— (x-k)² + ...
0! 1! 2!
項數越大,係數越小。縮小速度呈階乘倒數。縮小速度勝過多項式倒數、指數倒數。
順帶一提,第34項係數分母1/34! ≈ 3.38716e-39,已經小於浮點數最小值FLT_MIN ≈ 1.17549e-38。
只需保留開頭幾項,就跟f(x)相差無幾。但是注意到只在x = k的附近相差無幾。
f(k) f′(k) f″(k)
f(x) ≈ ————— (x-k)⁰ + ————— (x-k)¹ + ————— (x-k)²
0! 1! 2!
Taylor polynomial
每個partial sum各是一個Taylor polynomial。
先前的Bernstein polynomial不需要partial sum。習慣就好。
f(k)
————— (x-k)⁰
0!
f(k) f′(k)
————— (x-k)⁰ + ————— (x-k)¹
0! 1!
f(k) f′(k) f″(k)
————— (x-k)⁰ + ————— (x-k)¹ + ————— (x-k)²
0! 1! 2!
:
:
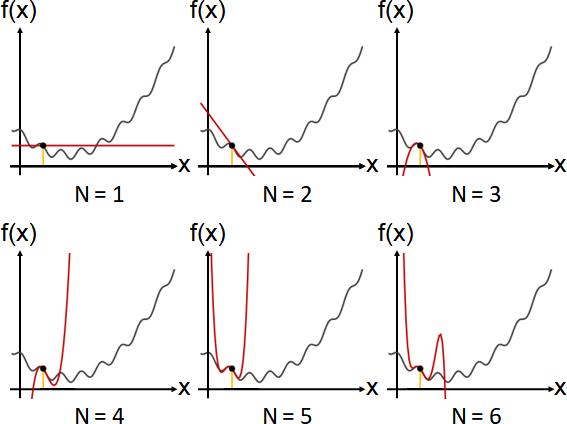
Taylor approximation
「泰勒近似」。近似函數是N個多項式的加權總和。
採用泰勒級數前N項。多項式是(x-k)ⁿ,權重是f⁽ⁿ⁾(k) / n!,索引值n從0到N-1。
自由調整k,以決定近似函數所在地點。k的幾何意義是平移量:k = 0是不平移、k = 1是往右平移一單位。
「Taylor approximation theorem」:N越大,越符合!
Taylor approximation vs. Hermite interpolation
Taylor approximation類似於「Hermite interpolation」,但是只有x = k的各階導數相等。
linear approximation(linearization)
「一次近似」或「一次化」。泰勒近似的特例,只取前2項。
f(k) f′(k)
f(x) = ————— (x-k)⁰ + ————— (x-k)¹ + ...
0! 1!
f(x) ≈ f(k) + f′(k) (x-k)
Taylor series又一種形式
泰勒級數可以改寫成各階導數f⁽ⁿ⁾(x)的加權總和。
f(x) (Δx)⁰ f′(x) (Δx)¹ f″(x) (Δx)²
f(x + Δx) = —————————— + —————————— + ——————————— + ...
0! 1! 2!
當x略微增減,得知f(x)如何增減。
從x處走一步,得知f(x)升降何處。
finite difference
順帶一提,微分、積分,可以使用泰勒級數,設計數學公式。
有限差分,源自泰勒級數前2項。甚至更多項。
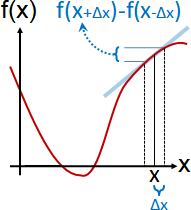
f(x) (Δx)⁰ f′(x) (Δx)¹ f″(x) (Δx)²
f(x + Δx) = —————————— + —————————— + ——————————— + ...
0! 1! 2!
f(x) (Δx)⁰ f′(x) (Δx)¹ f″(x) (Δx)²
f(x - Δx) = —————————— - —————————— + ——————————— - ...
0! 1! 2!
1st-order central derivative f(x+Δx) - f(x-Δx) ≈ 2 f′(x) Δx f′(x) ≈ [f(x+Δx) - f(x-Δx)] / 2Δx 2nd-order central derivative f(x+Δx) + f(x-Δx) ≈ 2 f(x) + f″(x) (Δx)² f″(x) ≈ [f(x+Δx) + f(x-Δx) - 2 f(x)] / (Δx)²
若Δx介於±1,則(Δx)ⁿ介於±1,則係數介於±1。
令Δx足夠微小,則係數迅速縮小、微不足道、無關緊要。只需保留開頭幾項,就跟正解相差無幾。
泰勒近似需要計算f(k) f′(k) f″(k) ...。如果難以手工推導公式解,那麼可以使用有限差分。
finite quadrature
有限求積,源自泰勒級數前2項。甚至更多項。
1st-order central integral f′(x) ≈ [f(x+Δx) - f(x-Δx)] / 2Δx f(x) ≈ [∫f(x+Δx) - ∫f(x-Δx)] / 2Δx f(x-Δx) ≈ [∫f(x) - ∫f(x-2Δx)] / 2Δx ∫f(x) ≈ ∫f(x-2Δx) + f(x-Δx) ⋅ 2Δx ∫f(x) ≈ [... + f(x-3Δx) + f(x-Δx)] ⋅ 2Δx
root finding
順帶一提,求根、求極值,可以使用泰勒級數,設計演算法。
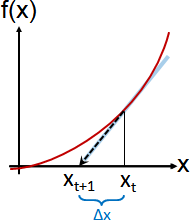
牛頓法求根,源自泰勒級數前2項。
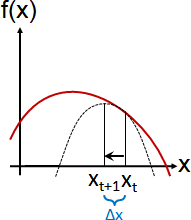
f(x) (Δx)⁰ f′(x) (Δx)¹
f(x + Δx) = —————————— + —————————— + ...
0! 1!
let f(x + Δx) = f(x) + f′(x) Δx 1st-order taylor expansion
let f(x + Δx) = 0 root position
f(x) + f′(x) Δx = 0
Δx = -f(x) / f′(x)
xₜ₊₁ - xₜ = -f(xₜ) / f′(xₜ) Newton's method for root finding
optimization
牛頓法求極值,源自泰勒級數前3項。
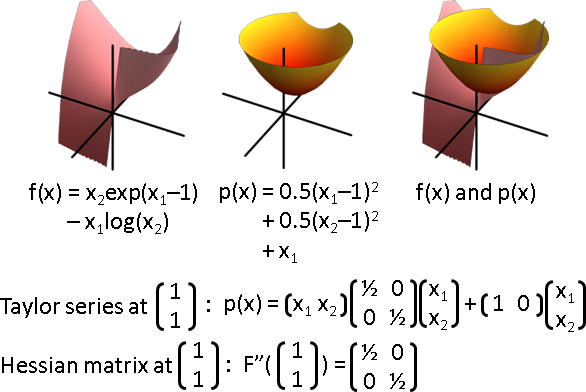
f(x) (Δx)⁰ f′(x) (Δx)¹ f″(x) (Δx)²
f(x + Δx) = —————————— + —————————— + ——————————— + ...
0! 1! 2!
let f(x + Δx) = f(x) + f′(x) Δx + ½ f″(x) (Δx)²
f(x + Δx) - f(x) = f′(x) Δx + ½ f″(x) (Δx)²
let d/dΔx [ f(x + Δx) - f(x) ] = 0 extremum position
d/dΔx [ f′(x) Δx + ½ f″(x) (Δx)² ] = 0
f′(x) + f″(x) Δx = 0
Δx = -f′(x) / f″(x)
xₜ₊₁ - xₜ = -f′(xₜ) / f″(xₜ) Newton's method for optimization
multivariable optimization
多元函數版本。x和Δx變成向量。
二次微分f″(x)是Hessian matrix。根據Hessian matrix屬於正定、負定、未定,推測x位於極小值、極大值、鞍點。

syms x y f = y*exp(x - 1) - x*log(y); taylor(f, [x, y], [1, 1], 'Order', 3)
g1 = Plot3D[y*Exp[x-1] - x*Log[y], {x, -3, 3}, {y, -3, 3}, PlotRange -> {-3, 3}, BoxRatios->{1,1,1}, ClippingStyle -> None, Mesh-> None, Axes->None, Boxed -> False, ColorFunction -> (ColorData["CherryTones"][Rescale[#3, {-2, 2}]] &)]; g2 = Plot3D[x + ((x-1)^2)/2 + ((y-1)^2)/2, {x, -3, 3}, {y, -3, 3}, PlotRange -> {-3, 3}, BoxRatios->{1,1,1}, ClippingStyle -> None, Mesh-> None, Axes->None, Boxed -> False, ColorFunction -> "SolarColors"];
f(x) f′(x)ᵀ Δx Δxᵀ f″(x)ᵀ Δx
f(x + Δx) = ———— + ————————— + ————————————— + ...
0! 1! 2!
xₜ₊₁ - xₜ = -f″(x)⁻¹ f′(x) Newton's method for multivariable optimization
constrained optimization
投影梯度法,約束函數進行泰勒近似,擷取泰勒級數前2項,以便迅速判斷是否偏離約束條件。
f(x) f′(x)ᵀ Δx
f(x + Δx) = ———— + ————————— + ...
0! 1!
c(x) ≥ 0 c(x + Δx) ≈ c(x) + (c′(x) dot Δx) ≥ 0
Padé approximation
Padé approximation
Taylor approximation進行微調。
優點:函數曲線抖動(Runge's phenomenon)變平緩。
泰勒近似的結果,再度近似。近似函數是多項式分式。
a₀x⁰ + a₁x¹ + a₂x²
c₀x⁰ + c₁x¹ + c₂x² + c₃x³ = ——————————————————
b₀x⁰ + b₁x¹
Taylor approximation
(when k = 0) polynomial fraction
令分子與分母的次方數相加,等於泰勒近似結果的次方數。
分子與分母的次方數習慣對半分、或者分子多一。
deg(c) = deg(a) + deg(b) deg(a) = deg(b) or deg(b) + 1
分母移項,展開,對應項係數相等,形成大量等式。
只取前deg(c) + 1項形成等式,令b₀ = 1,以得到唯一解。
(c₀x⁰ + c₁x¹ + c₂x² + c₃x³)(b₀x⁰ + b₁x¹) = a₀x⁰ + a₁x¹ + a₂x² ⎧ c₀b₀ = a₀ ⎨ c₀b₁ + c₁b₀ = a₁ ⎪c₀b₂ +c₁b₁ + c₂b₀ = a₂ ⎩c₀b₃ + c₁b₂ +c₂b₁ + c₃b₀ = 0
解法是兩個一次方程組。所有等式分成前deg(a) + 1道等式(等於a)、後deg(b)道等式(等於零)。先以後段等式解出b,再以前段等式解出a。
進階解法請見《Robust Padé Approximation via SVD》。