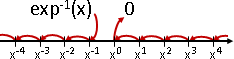
natural logarithmic function
自然指數函數的反函數
自然指數函數是嚴格遞增函數,擁有反函數。
自然指數函數的反函數,擁有多種寫法。畢竟可以進位和借位。
自然指數函數的反函數,經典的寫法是「Mercator series」。
(x-1)¹ (x-1)² (x-1)³
exp⁻¹(x) = —————— - —————— + —————— - ...... (0 < x ≤ 2)
1 2 3
1 ⎛x-1⎞¹ 1 ⎛x-1⎞² 1 ⎛x-1⎞³
exp⁻¹(x) = — ⎜———⎟ + — ⎜———⎟ + — ⎜———⎟ + ...... (x > 1/2)
1 ⎝ x ⎠ 2 ⎝ x ⎠ 3 ⎝ x ⎠
兩種計算方式:
一、二項式反演(拉格朗日展開的特例)。
二、函數複合、一次微分。
「自然指數函數的反函數」屬於「對數函數」
「指數函數的反函數」稱作「對數函數」。
對數函數:a的幾次方是x。a是任意數。
f(x) = loga(x)
對數函數的等價定義:輸入相乘等同輸出相加。
f(xy) = f(x) + f(y)
natural logarithmic function
「自然指數函數的反函數」重新稱作「自然對數函數」。
(x-1)¹ (x-1)² (x-1)³
ln(x) = logₑ(x) = —————— - —————— + —————— - ...... (0 < x ≤ 2)
1 2 3
並且重新設計數學符號:
ln(x)稱作「自然對數函數」。
e稱作「歐拉數」。
natural logarithmic function上界
近似公式,但是不等於。證明請見維基百科。
(x-1)¹ (x-1)² (x-1)³ (x-1)ⁿ
ln(x,n) = —————— - —————— + —————— - ... + ——————
1 2 3 n
1 1 1 1
< ——— + ——— + ——— + ... + ———
1 2 3 n
(x-1)¹ (x-1)² (x-1)³
ln(x) = —————— - —————— + —————— - ......
1 2 3
1 1 1
< ——— + ——— + ——— + ......
1 2 3
「自然指數函數的反函數」恰是x⁻¹的積分
反函數即是函數圖形沿著45°斜線翻面。
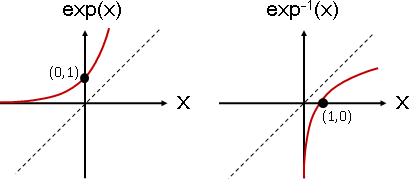
斜率是高度除以寬度。反函數翻轉高度和寬度,讓斜率變成倒數。以此推導出exp⁻¹(x)的斜率是x⁻¹。
斜率就是微分結果。以此推導出exp⁻¹(x)是x⁻¹的積分。
exp⁻¹(x) = y
d/dx exp⁻¹(x) = 1 / (d/dy exp(y)) 反函數的斜率變成倒數
d/dx exp⁻¹(x) = 1 / exp(y) 微分不動點
d/dx exp⁻¹(x) = 1 / x exp(y) = x
exp⁻¹(x) = ∫ (1 / x) dx
「自然指數函數的反函數」完成了整數次方的微積分
微分讓次方值減一,唯一例外是0次方。0次方微分之後,不是-1次方,而是回歸虛無。
積分讓次方值加一,唯一例外是-1次方。-1次方積分之後,不是0次方,而是涵蓋萬物。「自然指數函數的反函數」涵蓋所有非負次方。