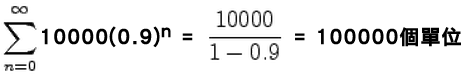Sequences and Series

將一個等差數列各項依序加起來，就稱為一個等差級數
＠s_n=(n(a₁+a_n)) ⁄ 2 (已知首項、末項及項數)
＠s_n=(n[2a₁+(n-1)d]) ⁄ 2 (以隻首項、公差及項數)
＠第n項可以用級數來算，a_n=s_n-s_(n-1)

將一個等比數列各項依序加起來，就稱為一個等比級數
＠s_n=[a₁ (rⁿ-1)] ⁄ (r-1)或者是s_n=[a₁ (1-rⁿ)] ⁄ (1-r)
＠第n項可以用級數來算，a_n=s_n-s(n-1)

將小數代表1/3是個簡單的例子可以寫成無限加總。

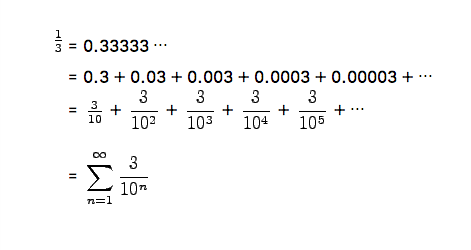
這最後的符號∑稱為加總符號或總和符號。
有限和 a₁ + a₂ + a₃ + ^... + a_n 可以寫成

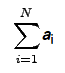
字母 i 是總和的指標，而且 1 和 n 分別是總和的下極限和上極限。
利用總和符號

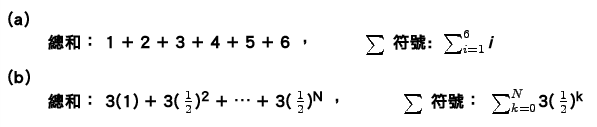
無窮總和
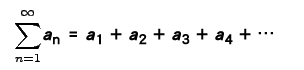
稱做一個無窮級數。這數列的部分和是一個極數標記為

考慮一個無窮級數 a₁ + a₂ + a₃ + ^... 。如果這個序列的部分和 {s_n} 收斂到 s ，則這個無窮級數收斂到 s 。
這極限被標註為

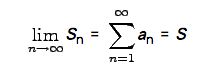
並且 s 被稱做為這個極數的和。如果這個序列的極限是部份和 {s_n} 不存在，則這個級數發散。

如果 a 是一個非負實數，則無窮級數

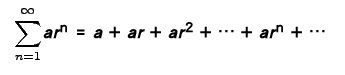
被稱做以公比為 r 的幾何級數
幾何級數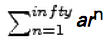， n 項部分和是

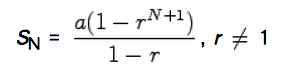
市場安穩定的模型
一個製造商每年賣出10000單位的產品.再任一給定的年份中，每個單位有百分之10的製造減少率。
經過一年後你期望只有9000個單位產生在之前一年10000個單位仍被使用中.經過下一年，
這數字又下降了百分之10到8100個單位產生，繼續以此類推。有多少個單位在20年之後是被使用中？
有多少單位是穩定的被使用?如果可以，找出穩定的點.
解:你可以用幾何數列模擬這個情況,如下圖。

經過 20 年後，被使用的單位數字將是

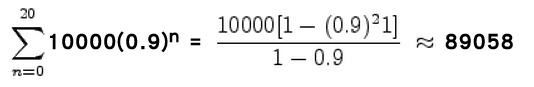
在圖10.3有一個說明，被使用的單位數字會趨近於一個安定的點。