Sequences and Series

在一個數列中，如果任意相鄰兩項中的後項減前項之差都相等，我們就稱此數列為等差數列，而這個差稱為公差。
＠公差：公差代表著每項之間的差，例如首項為a，公差為d，則第二項為a+d，第三項為a+2d…..，第n項為a+(n-1)d
＠等差中項：從第二項開始，前一項加後一項的和的値為該項的兩倍，意同於

在一個數列中，其後項比前項的比值為一個定值，我們就把這些有順序的數列叫做等比數列，而兩項的比值就稱為公比。
＠公比：公比代表著兩項之間的比值，例如首項為a，公比為r，則第二項為ar，第三項為ar^2…，第n項為ar^(n-1)，意同於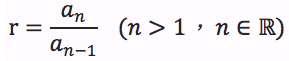

＠等比中項：從第二項開始，前一項與後一項的乘積為該項的平方，意同於

又譯為「費波那契數列」或「斐波那契序列」；中世紀的意大利數學家費波那契（Leonardo Fibonacci，西元1170-1250年）發現了這樣的一個數列：1、1、2、3、5、8、13、……；後人稱之為費氏數列，並且對其性質加以研究與應用、發揚光大。
費氏數列是是由一連串的數字所組成的（假設為 　a1、a2、a3……an-1、an），而且這串數字之間具有一定的規則，就是：每一個數字必須是前兩個數字的和 (an = an-1 + an-2 )。
後人也發現費氏數列有一些耐人尋味的有趣性質，例如：當費氏數列一直算到很大或無限大的時候 ( 也就是 n值無限大時 )，後項除以前項的極限是黃金分割的值；而數學家也發現在大自然中，可以費氏數列來描述某些植物的生長規則，例如雛菊的花瓣的生長數目。

即一數列，若其倒數所成的數列為等差數列，則此數列為調和數列。
例如：2,5,8,11,14.....成等差數列，則1/2,1/5,1/8,1/11,1/14.....成調和數列

又叫高階等差數列、質數相關數列，是指二階或二階以上的等差數列。把一個數列的所有後項與前一項之差組成一個新的數列，如果這個新的數列是普通等差數列，原數列就是二階等差數列。例如，數列：１、２、４、７、１１、１６、２２、２９．．．它的前後項之差所組成的新數列：１、２、３、４、５、６、７．．．為普通等差數列，所以原數列為二階等差數列。
依此類推，把一個數列的所有後項與前一項之差組成一個新的數列，再把這個新的數列的所有後項與前一項之差組成另一個新的數列，如此進行下去，直到最後的數列如果是普通等差數列，那麼原數列就是多階等差數列。
普通等差數列可以視為一階等差數列，因而常數數列實際就是零階等差數列。
舉一個簡單的例子
有一數列1，6，15，28，45，66，91，120，153，190
後項減前項後，得
6-1，15-6，28-15，45-28，66-45，91-66，120-91，153-120，190-153
即5，9，13，17，21，25，29，33，37 為一等差數列
我們就稱 1，6，15，28，45，66，91，120，153，190 為一 階差數列

OEIS A274119 數列的故事
一切的故事從一題 2003 倍數開始，題目是：
請問 (1 x 3 x 5 x ..... x 2001) + (2 x 4 x 6 x ..... x 2002) 是否為 2003 的倍數？
利用 modular arithmetic 可以輕易證明答案是整除的，這方法是網友 z423x5c6 所提供。簡單說除法餘數可以加減乘除，如以下範例：
5 / 11 = 0 ... 5
2 / 11 = 0 ... 2
(5 + 2) / 11 = 0 ... 7
(5 x 2) / 11 = 0 ... 10
(5 + 11) / 11 = 1 ... 5
(5 - 11) / 11 = 0 ... -6

A / B = C ... D 在數學上除法餘數會用右式表示，A ≡ D mod B
只要證明 (1 x 3 x 5 x ..... x 2001) + (2 x 4 x 6 x ..... x 2002) ≡ 0 mod 2003，就可解出來，
(1 x 3 x 5 x ..... x 2001) + (2 x 4 x 6 x ..... x 2002)
≡ [1 x 3 x 5 x ..... x 2001 + (2-2003) x (4-2003) x (6-2003) x ..... x (2002-2003)] mod 2003
≡ [1 x 3 x 5 x ..... x 2001 + (-2001) x (-1999) x (-1997) x ..... x (-1)] mod 2003
≡ [1 x 3 x 5 x ..... x 2001 - 2001 x 1999 x 1997 x ..... x 1] mod 2003
≡ 0 mod 2003 整除

在求解時，發現以下規則
(1 + 2) / 3 = 1
(1 x 3 x 5 + 2 x 4 x 6) / 7 = 9
(1 x 3 x 5 x 7 x 9 + 2 x 4 x 6 x 8 x 10) / 11 = 435
1, 9, 435, ... 在 OEIS 是一個全新數列，名為 A273889

關於OEIS，是由數學家尼爾·斯洛恩 (Neil James Alexander Sloane) 在1960年代中開始搜集整數數列，於 1996 年設置網站供大眾查閱，每年有上萬件各類研究者提供新數列登錄。

OEIS A273916 數列的故事 (Bingo-4)
如同五子棋，在棋盤上只要四子就可以一連線，可以直線、橫線、45度斜線，請問最少需要幾顆子可以排列三連線？(超過四子的連線不計，來自四子三連線)
當這問題被貼文到研發養成所的訓練數學感系列文章經過熱烈討論之後，發現四子連線的問題還隱藏著一個未被發現的數列，因此這系列數列研究從此展開。
這就是 A273916 數列的由來。
0, 4, 7, 9, 11, 12, 12, 14, 15, 16, 16, 18, 19, 20, 22, 24, ...