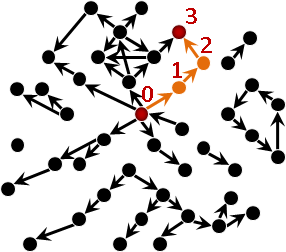
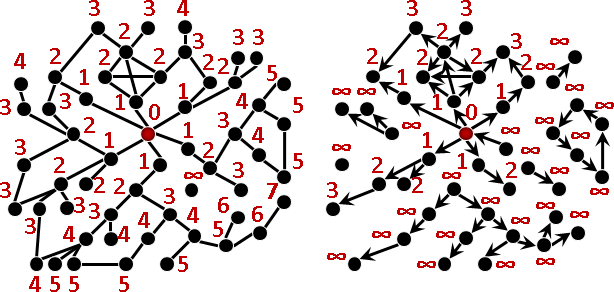
intersection graph
圖用來表達兩兩之間的關係。例如一群人,我們可以建立「朋友關係」的圖,兩個人是朋友就連一條邊,兩個人不是朋友就沒有邊。只要是兩兩之間的關係,就得以轉化成圖,運用圖論知識來分析問題。
其中有個值得一提的關係是「交集關係」,是聯集交集的那個交集。兩個東西有交集就連一條邊(交集不是空集合)、沒交集就沒有邊(交集是空集合),最後得到的圖叫做「交集圖」。
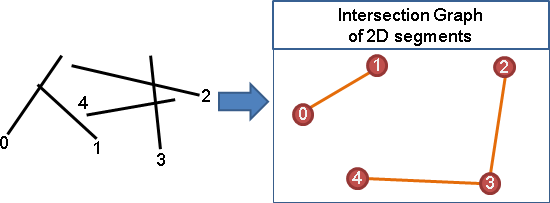
例如一堆線段,把互相接觸的線段,表示成圖:
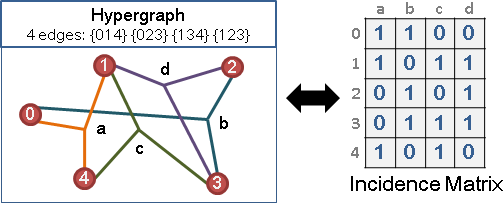
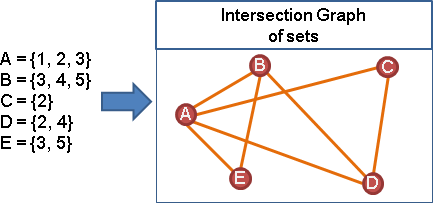
例如一堆集合,把有交集的集合,表示成圖:
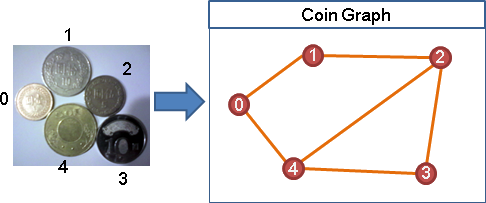
比較特別的交集圖,數學家會特地取名。例如一堆硬幣,平鋪在桌上,把互相接觸的硬幣,表示成圖,稱作coin graph。數學家發現硬幣圖和平面圖兩者完全等價,每一種平面圖都可以利用硬幣接觸兜出來。
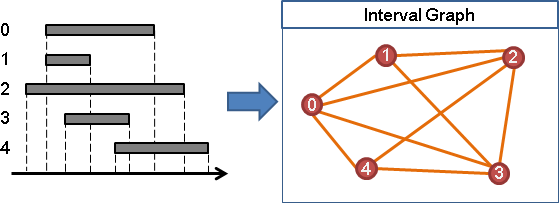
例如行程表,把撞期的行程,表示成圖,稱作interval graph,有著很特別的數學性質。
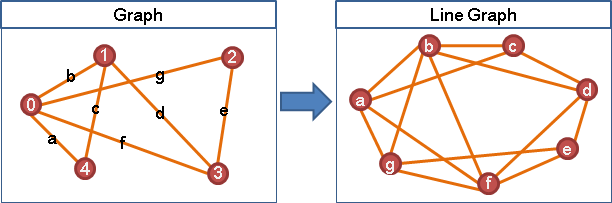
例如一張圖論的圖,把共用端點的邊,表示成圖,稱作line graph。
為什麼數學家特別重視交集圖呢?我也不知道。
很多人把交集圖看做是一個物品。但是交集圖其實是一種變換的概念,可以看做是一個函數。
dependency graph【尚無正式名稱】
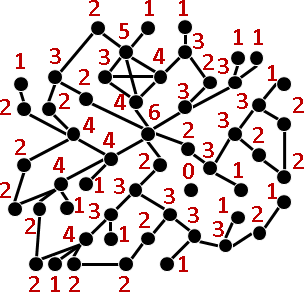
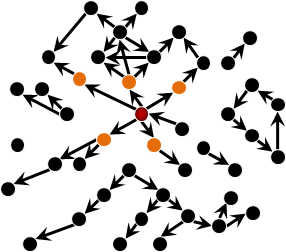
除了「交集關係」之外,數學家也很重視「依賴關係」。把各個東西的仰賴對象表示成圖,最後得到的圖叫做「依賴圖」。
例如一堆不等式,把變數大小關係,表示成圖:
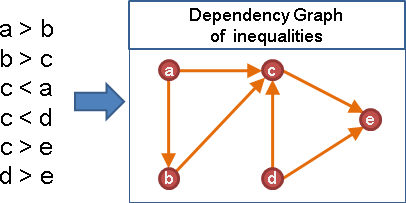
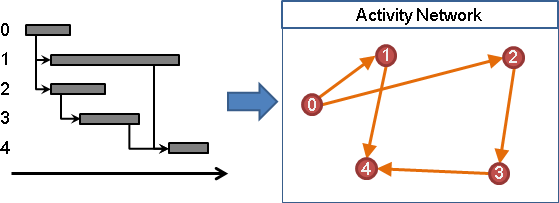
比較特別的依賴圖,數學家會特地取名。例如專案管理領域,把工作先後次序,表示成圖,稱作「activity network」。
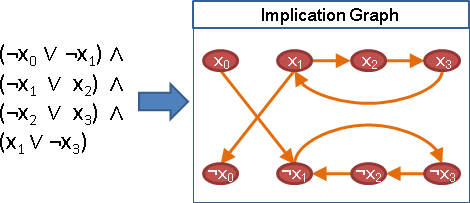
例如2-SAT問題,把各個clause裡面的兩個變數的取捨關係,表示成圖,稱作「implication graph」。
交集圖是無向圖、依賴圖是有向圖,剛好一對。
UVa 10926
subgraph / supergraph
一張圖,刪除一些點、一些邊,得到的圖稱作「子圖」。
原圖(沒有刪除)、空圖(完全刪除),也算是「子圖」。
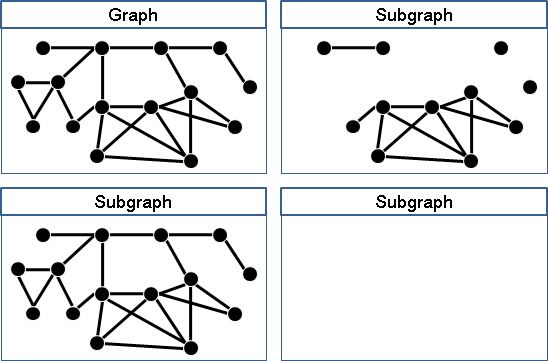
一張圖,增加一些點、一些邊,得到的圖稱作「父圖」。
原圖(沒有增加)也算是「父圖」。
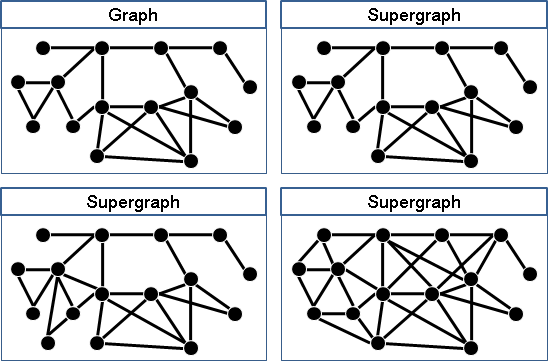
subgraph和supergraph是相對的。如果A是B的子圖,那麼B就是A的父圖。我們習慣只講子圖,講一個就等於兩個都講了。
induced subgraph / induced supergraph
一張圖,保留一些點、以及這些點之間的所有邊,得到的圖稱作「導出子圖」。
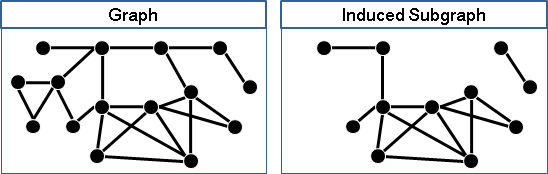
一張圖,增加一些點、一些邊,但是不在原本的點之間增加邊,使得原本的圖是導出子圖,得到的圖稱作「導出父圖」。
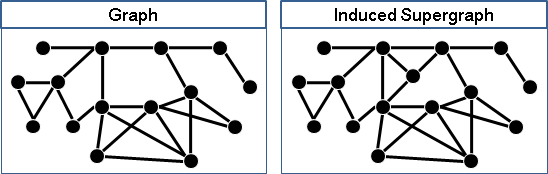
induced subgraph和induced supergraph是相對的。如果A是B的導出子圖,那麼B就是A的導出父圖。我們習慣只講導出子圖,講一個就等於兩個都講了。
minor / subdivision
一張圖,收縮一些邊、合併一些點,得到的圖稱作minor。
收縮的邊,有人視情況刪除,也有人視情況不刪除、而變成連向自己的邊。
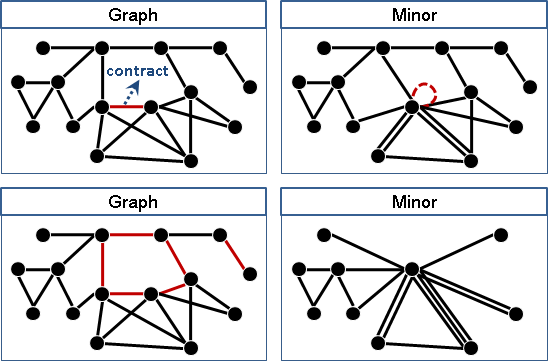
一張圖,在邊上植入點,得到的圖稱作subdivision。
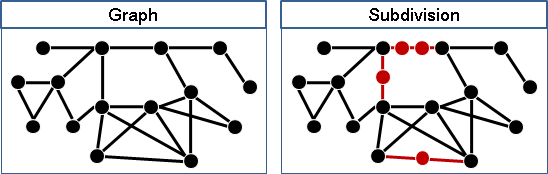
minor和subdivision是相對的。一般只討論minor。
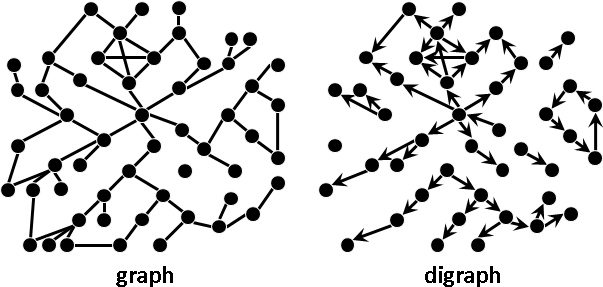
oriented graph / underlying graph
一張無向圖,無向邊改成有向邊,稱作「定向圖」。
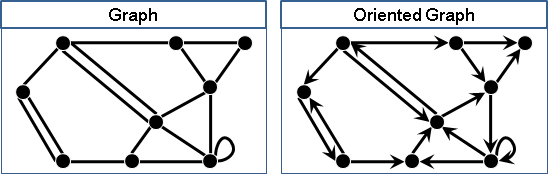
一張有向圖,有向邊改成無向邊,稱作「底圖」。
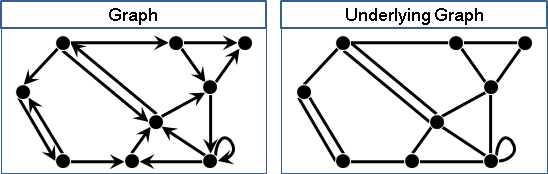
定向圖和底圖是相對的。一般只討論定向圖。
complement graph(complement)
一張圖,兩點之間沒邊變有邊、有邊變沒邊,稱作「補圖」。
原圖暨補圖的所有邊,合起來是完全圖。
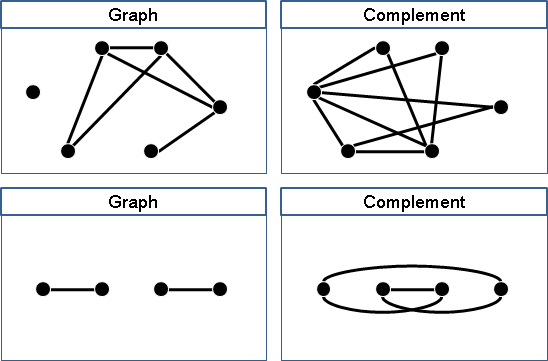
朋友變仇人、有關變無關,整個相反顛倒,就是補圖的用處。
reverse graph(transpose)
一張有向圖,邊的方向顛倒,稱作「反向圖」。
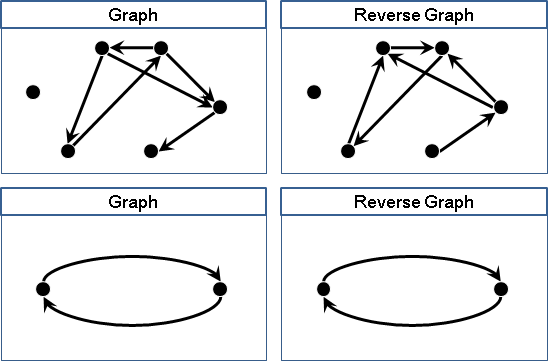
主動變被動、前進變後退,整個相反顛倒,就是反向圖的用處。
line graph
一張圖當中,觀察邊與邊關係,相鄰的邊表示成一張圖,稱作「線圖」。
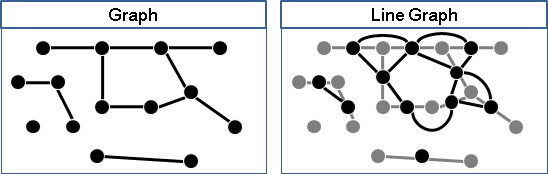
UVa 10988 11175
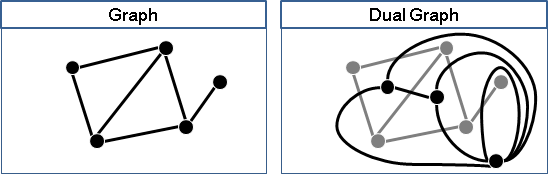
dual graph
一張平面圖當中,觀察面與面關係,共邊的面表示成一張圖,稱作「對偶圖」。詳情請參考「planar graph」。