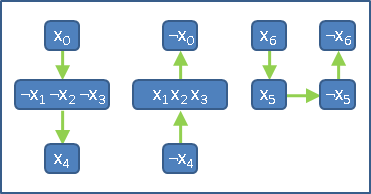
connected component（maximal connected subgraph）
（1-connected component in undirected graph）

譯作「連通分量」、「連通成分」、「連通元件」、「連通單元」，簡稱「分量」，沒有正式翻譯。

當一張無向圖不連通、分隔成幾個區塊的時候，每一個區塊都是一個「連通分量」。一個獨立的點也是一個連通分量。

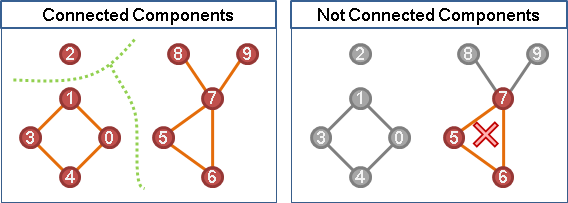
一張無向圖的連通分量們，不可能互相重疊。一個連通分量是指在連通的情況下，點數盡量最多、擴展範圍最大的一個子圖；因此，從一個連通分量當中，切下一小塊仍舊連通的子圖，並不能叫做連通分量。

運用graph traversal就能找到一張無向圖的所有連通分量。

UVa 459 10765

biconnected component（block）
（2-vertex-connected component in undirected graph）

一張無向圖上，不會產生關節點的連通分量，稱作「雙連通分量」。一張無向圖的雙連通分量們，通常會互相重疊，重疊的部分都是原圖的關節點。

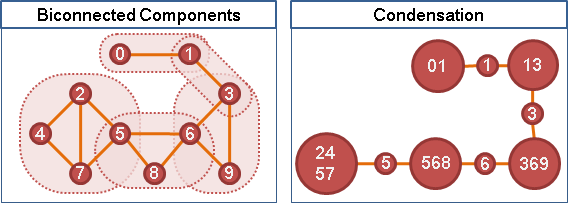
把一個雙連通分量視作一個點，把一個關節點也視作一個點，凡有接觸就添上一條邊，如此可以建立出一棵樹，通常稱作block-cutvertex tree或者block-cutvertex graph。

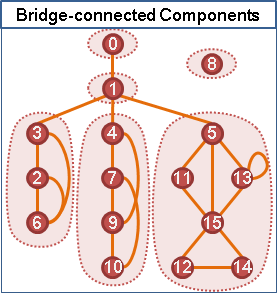
bridge-connected component
（2-edge-connected component in undirected graph）

一張無向圖上，不會產生橋的連通分量，稱作「橋連通分量」。

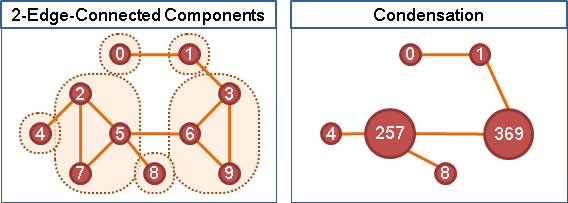
兩個點之間沒有橋，就至少有兩條不同的路徑。這兩條路徑勢必形成一個環。一個橋連通分量，想必是由很多環交疊而成的。

把一個這樣的連通分量視作一個點，凡有接觸就添上一條邊，如此可以建立出一棵樹。

ICPC 5135 4839 7605

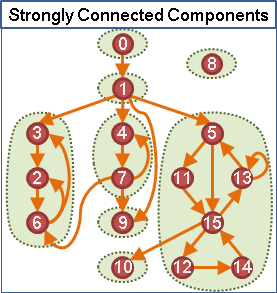
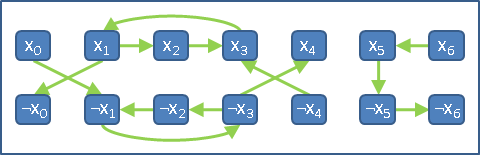
strongly connected component
（1-connected component in directed graph）

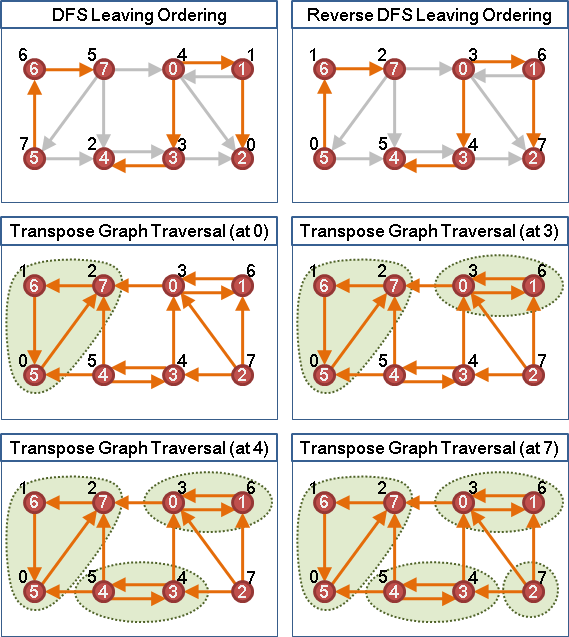
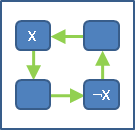
一張有向圖的「強連通分量」，是所有兩點之間，雙向皆有路可通的連通分量。一張有向圖的強連通分量們，不可能互相重疊。

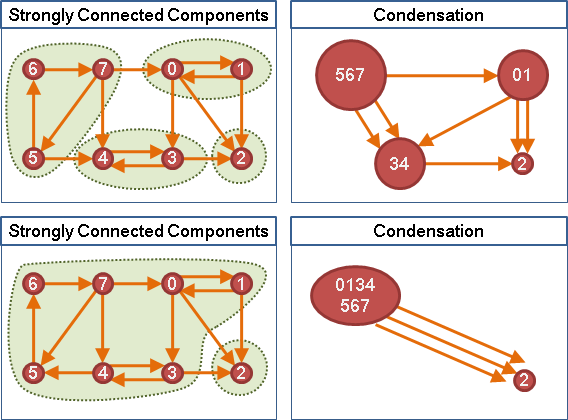
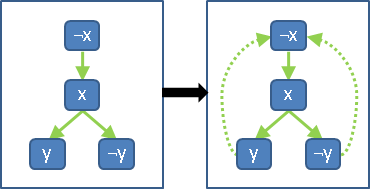
兩個點來回都有路徑，這兩條路徑勢必形成一個有向環。一個強連通分量，想必是由很多有向環交疊而成的。

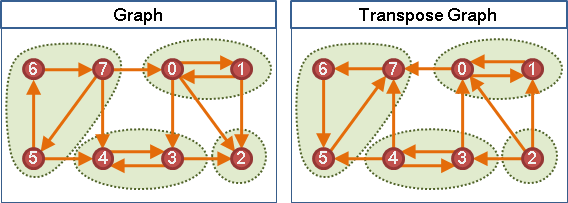
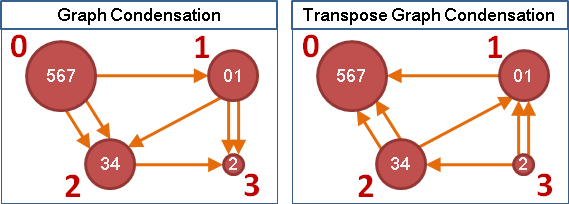
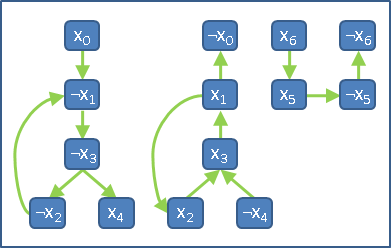
要是把一張圖的各個強連通分量，各自收縮成一個點，如此圖上就沒有環，形成有向無環圖（DAG）。這個手法很有用處──沒有環的圖，常常會有效率極佳、令人眼睛一亮的演算法。當遇到一張有環的圖，不妨先把每個強連通分量統統收縮，簡化問題的複雜程度。

UVa 11504 11709 11770 11838

weakly connected component

一張有向圖的「弱連通分量」，是所有兩點之間，至少單向有路可通的連通分量。一張有向圖的弱連通分量們，通常會互相重疊。

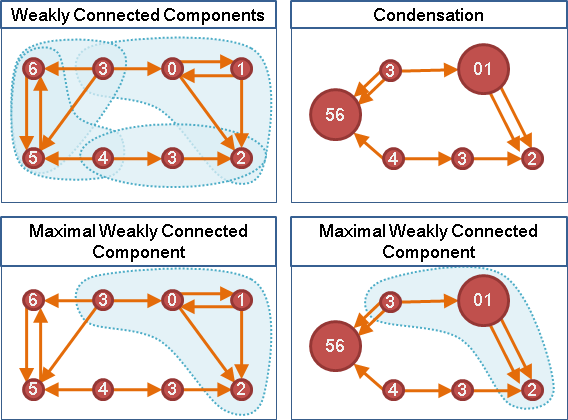
一個弱連通分量，可以看作是強連通分量的縮圖當中的一條有向路徑。要找最大的弱連通分量，即是縮圖當中，涵蓋最多原點的一條有向路徑。

UVa 11324

演算法

一張無向圖，找到所有的bridge-connected component。亦可進一步收縮所有的BCC、收縮所有的環，讓原圖變成一叢森林。

一張有向圖，找到所有的strongly connected component。亦可進一步收縮所有的SCC、收縮所有的環，讓原圖變成一張有向無環圖。

為什麼要收縮呢？當圖上有環，難以設計有效率的演算法。收縮所有的環，讓圖變成樹、有向無環圖，就容易解決問題了！

無向圖：
尋找所有的bridge-connected component、收縮所有的環

利用尋找所有橋的演算法，輔以堆疊，找到所有的BCC。

一、實施DFS。
二、拜訪階段，
　　針對每一個點，計算自身與子孫所能觸及的最高祖先。
　　（觸及是指：不斷往下走tree edge、往上走back edge。）
三、回溯階段，
　　每當發現某一點恰是最高祖先，即表示此點與子孫已經形成BCC。
　　從堆疊之中刪除BCC，避免再次處理。

時間複雜度等於一次DFS的時間。圖的資料結構為adjacency matrix是O(V²)；圖的資料結構為adjacency lists是O(V+E)。

int adj[9][9]; // 記錄邊數，支援多重邊 int visit[9], low[9], t = 0; int stack[9], top = 0; // 堆疊 int contract[9]; // 每個點收縮到的點 void DFS(int i, int p) { visit[i] = low[i] = ++t; stack[top++] = i; // push i for (int j=0; j<9; ++j) if (adj[i][j]) { // tree edge if (!visit[j]) DFS(j, i); // tree/back edge if (!(j == p && adj[i][j] == 1)) low[i] = min(low[i], low[j]); } // 形成BCC。 // BCC裡面，最早拜訪的點是i點。 if (visit[i] == low[i]) { // cout << "block:"; int j; do { j = stack[--top]; // pop j // cout << j; contract[j] = i; } while (i != j); } } void tarjan() { memset(visit, 0, sizeof(visit)); t = 0; for (int i=0; i<9; ++i) if (!visit[i]) DFS(i, i); }

有向圖：
尋找所有的strongly connected component、收縮所有的環

與無向圖幾乎相同。不必擔心多重邊的問題，但是要小心處理forward edge和cross edge。

一、實施DFS。
二、拜訪階段，
　　針對每一個點，計算自身與子孫所能觸及的最高祖先。
　　觸及是指：不斷走任意邊，但是不能走到曾經形成的SCC。
　　（forward edge和cross edge可能連往已經移除的SCC，不得計算。）
三、回溯階段，
　　每當發現某一點恰是最高祖先，即表示此點與子孫已經形成SCC。
　　從堆疊之中刪除SCC，避免再次處理。

bool adj[9][9]; int visit[9], low[9], t = 0; int stack[9], top = 0; // 堆疊 bool instack[9]; // 記錄DFS forest目前尚存哪些點 int contract[9]; // 每個點收縮到的點 void DFS(int i) { visit[i] = low[i] = ++t; stack[top++] = i; instack[i] = true; for (int j=0; j<9; ++j) if (adj[i][j]) { // tree edge if (!visit[j]) DFS(j); // tree/back/forward/cross edge // 已經遍歷過、但是尚未形成SCC的點 if (instack[j]) low[i] = min(low[i], low[j]); } // 形成SCC，從目前的DFS forest移除它。 // SCC裡面，最早拜訪的點是i點。 if (visit[i] == low[i]) { int j; do { j = stack[--top]; instack[j] = false; contract[j] = i; } while (j != i); } } void tarjan() { memset(visit, 0, sizeof(visit)); t = 0; for (int i=0; i<9; ++i) if (!visit[i]) DFS(i); }

演算法

一張有向圖，找到所有的strongly connected component。亦可進一步收縮所有的SCC、收縮所有的環，讓原圖變成一張有向無環圖。

原圖，顛倒每一條邊的方向，得到新圖。所有SCC的位置依舊相同！

縮圖亦然！原縮圖、新縮圖都是有向無環圖。以原縮圖的拓樸順序，遍歷新縮圖，依序摘下每個點，每個點都是一個SCC。而且只有入邊、沒有出邊。

改以尚未收縮的原圖、新圖來詮釋。以原圖的「偽」拓樸順序，遍歷新圖，依序摘下每個連通分量，每個連通分量都是一個SCC。而且沒有出邊，不怕走過頭。

原圖有環，沒有拓樸順序，只好以偽物代替：「DFS離開點的順序，然後頭尾顛倒」或簡述為「DFS離開點的逆序」。雖然這個順序既非原圖、亦非縮圖的拓樸順序，但是可以優先遇見應該摘下的連通分量。

一、原圖實施DFS，找偽拓樸順序。
　　（每一棵SCC子樹，必然連續遍歷。）
二、新圖實施DFS/BFS，以偽拓樸順序找連通分量。
　　每一棵DFS tree/BFS tree，對應到每一個SCC。
　　（確認哪些點是同一個SCC。）

時間複雜度是兩次DFS的時間，以及顛倒所有邊的時間。

圖的資料結構為adjacency matrix，不必變動資料結構就可以達到顛倒所有邊的效果，時間複雜度O(V²)；圖的資料結構為adjacency lists，需要特地顛倒所有邊，時間複雜度O(V+E)。

int adj[9][9]; // adjacency matrix bool visit[9]; // DFS visit record vector<int> finish; // DFS離開點的順序 int scc[9]; // 每個點的強連通分量編號 void DFS1(int i) { visit[i] = true; for (int j=0; j<9; ++j) if (adj[i][j] && !visit[j]) DFS1(j); finish.push_back(i); } void DFS2(int i, int c) { cout << "第" << c << "個強連通分量"; cout << "包含第" << i << "點"; scc[i] = c; // 設定第i點屬於第c個強連通分量 visit[i] = true; for (int j=0; j<9; ++j) if (adj[j][i] && !visit[j]) // 顛倒所有邊的方向 DFS2(j, c); } void kosaraju() { finish.clear(); memset(visit, false, sizeof(visit)); for (int i=0; i<9; ++i) if (!visit[i]) DFS1(i); int c = 0; memset(visit, false, sizeof(visit)); for (int i=9-1; i>=0; --i) if (!visit[finish[i]]) // 原圖的偽拓撲順序 DFS2(finish[i], c++); // 找到一個強連通分量 } int adj[9][9]; bool visit[9]; vector<int> finish; // 依照離開順序排好所有點 int contract[9]; // 每個點收縮到的點 void DFS1(int i) { if (visit[i]) return; visit[i] = true; for (int j=0; j<9; ++j) if (adj[i][j]) DFS1(j); finish.push_back(i); } void DFS2(int i, int p) { if (visit[i]) return; visit[i] = true; for (int j=0; j<9; ++j) if (adj[j][i]) // 顛倒所有邊的方向 DFS2(j, i); contract[i] = p; // 收縮至第p點 } void kosaraju() { finish.clear(); memset(visit, false, sizeof(visit)); for (int i=0; i<9; ++i) DFS1(i); memset(visit, false, sizeof(visit)); for (int i=9-1; i>=0; --i) DFS2(finish[i], finish[i]); }

有向圖：尋找所有的2-connected component

《Finding 2-Edge and 2-Vertex Strongly Connected Components in Quadratic Time》

O(V²)。

有向圖：尋找所有的2-connected component

《Faster Algorithms for Computing Maximal 2-Connected Subgraphs in Sparse Directed Graphs》

O(EsqrtE)。

有向圖：在線尋找所有的2-connected component

《Incremental Strong Connectivity and 2-Connectivity in Directed Graphs》

O(VE)。

兩個至少選一個

首先介紹嘮叨媽媽和偏食小孩的討價還價問題。

青椒、菠菜至少選一個。青椒、番茄至少選一個。番茄、苦瓜至少選一個。苦瓜、菠菜至少選一個。不吃苦瓜、不吃青椒，至少選一個。選擇哪些菜色，才能成全媽媽的愛心，滿足小孩的任性？

2-satisfiability（2-SAT）

邏輯學有一個相似的問題。

變數X₀、X₁、……，變數值true或false。變數可以重複出現。變數可以加上not。括號之間是and，括號裡面是or，格式是固定的。

括號之間是and：每個括號都是true，整個式子才是true。

括號裡面是or：「左右皆true」或者「左true右false」或者「右true左false」，整個括號才是true。

如何設定變數值，讓整個式子成為true呢？

2-satisfiability另一種觀點

N個變數。每個變數都要設定數值為true或false。

一個變數X，要嘛X = true，要嘛X = false。換句話說，要嘛X = true，要嘛¬X = true。兩個元件X與¬X二選一。

N個變數，一共2N個元件。最後選出N個元件。

一個括號裡面有兩個元件，括號必須成為true。

正向思考：左右皆選、左選右不選、左不選右選。

可選可不選。這樹立了模稜兩可的規則，難以設計演算法。

逆向思考：不選這個，就必須選另外一個。

一定要選。這樹立了一定要遵守的規則，容易設計演算法。

以有向圖作為模型

把元件之間的「依賴關係」建立成有向圖。

一、依序處理每個括號。
　甲、變數不同。例如(X or Y)。
　　回、不選X（選了¬X），就一定要選Y：建立一條有向邊¬X → Y。
　　回、不選Y（選了¬Y），就一定要選X：建立一條有向邊¬Y → X。
　乙、變數相同。例如(X or X)。
　　回、一定要選X，一定不能選¬X：建立一條有向邊¬X → X。
　　　　（一旦選¬X，就連帶選X，產生矛盾。只好選X。） 
　丙、變數相同，一正一反。例如(X or ¬X)。
　　回、無論選X或選¬X都行：不必建立邊。

判斷是否有解

無解⇔遞移閉包上必有一個環同時穿過X與¬X。證明如下。

(⇐)選了一個點，可及之處也得選。X與¬X必須二選一。當X與¬X同屬一環，無論選哪一個，都會連帶選到對方，導致無解。

(⇒)引發無解的情況是X必選，而X同時可及Y與¬Y。既然X⤳Y，則同時存在逆否命題¬Y⤳¬X。既然X⤳¬Y，則同時存在逆否命題Y⤳¬X。最後使得X和¬X同屬一環。

實作時，判斷X與¬X是否在同一個SCC即可。SCC裡面是一群交織的環，SCC之間沒有環。

找出其中一組解

依序檢查每一對元件X與¬X。若是祖孫，則選擇孫，避免矛盾；若不是祖孫，則任一皆可，但是必須避免跟先前元件產生衝突。

可以找出字典順序最小的解。時間複雜度O(VE)。

一、建立有向圖。
二、依序判斷每一對元件X與¬X何者為解：
　甲、嘗試X作為解：若X可及之處存在非解者，則X非解。
　乙、嘗試¬X作為解：若¬X可及之處存在非解者，則¬X非解。
　丙、確認X與¬X何者為解之後，將其可及之處全數標記為解。

const int N = 10; // 變數數量 bool adj[20][20]; // adjacency matrix int visit[20]; // DFS visit record int sat[20]; // 解 int not(int a) {return a<N ? a+N : a-N;} //int not(int a) {return a&1 ? a : a+1;} //int not(int a) {return a^1;} bool dfs_try(int i) { if (visit[i] == 1 || sat[i] == 1) return true; if (visit[i] == 2 || sat[i] == 2) return false; visit[i] = 1; visit[not(i)] = 2; for (int j=0; j<N+N; ++j) if (adj[i][j] && !dfs_try(j)) return false; return true; } void dfs_mark(int i) { if (sat[i] == 1) return; sat[i] = 1; sat[not(i)] = 2; for (int j=0; j<N+N; ++j) if (adj[i][j]) dfs_mark(j); } void two_satisfiability() { // 一次輸入一個括號 memset(adj, false, sizeof(adj)); int a, b; while (cin >> a >> b) { map[not(a)][b] = true; map[not(b)][a] = true; } // 找出一組解 for (int i=0; i<N; ++i) { memset(visit, 0, sizeof(visit)); if (dfs_try(i)) {dfs_mark(i); continue;} memset(visit, 0, sizeof(visit)); if (dfs_try(not(i))) {dfs_mark(not(i)); continue;} // 無解則立即結束。 return; } // 印出一組解。 for (int i=1; i<N; ++i) if (sat[i] == 1) cout << i; else /*if (sat[i] == 2)*/ cout << "not" << i; }

找出其中一組解

採用逆向拓樸順序。時間複雜度O(V+E)。

一、建立有向圖。
二、尋找所有SCC。
三、收縮每個SCC，成為有向無環圖DAG。
　　（同一個SCC裡面的點，必須同進退；要嘛全選，要嘛全不選。）
四、尋找縮圖的拓樸順序。
五、在縮圖上，以逆向拓樸順序，設定解。

const int N = 10; bool adj[20][20]; int visit[20]; int sat[20]; int finish[20], scc[20], n = 0; void DFS1(int i) { visit[i] = true; for (int j=0; j<N+N; ++j) if (map[i][j] && !visit[j]) DFS1(j); finish[n++] = i; } void DFS2(int i) { scc[i] = n; visit[i] = true; for (int j=0; j<N+N; ++j) if (map[j][i] && !visit[j]) DFS2(j); } void two_satisfiability() { // 一次輸入一個括號 memset(adj, false, sizeof(adj)); int a, b; while (cin >> a >> b) { map[not(a)][b] = true; map[not(b)][a] = true; } // Kosaraju's algorithm：尋找拓撲順序。 n = 0; // 時刻 memset(visit, false, sizeof(visit)); for (int i=0; i<N+N; ++i) if (!visit[i]) DFS1(i); // Kosaraju's algorithm：找出強連通分量。 n = 0; // 強連通分量的編號 memset(visit, false, sizeof(visit)); for (int k=N+N-1; k>=0; --k) { int i = finish[k]; if (!visit[i]) DFS2(i), n++; } // 檢查是否有解，無解則立即結束。 for (int i=0; i<N; ++i) if (scc[i] == scc[inv(i)]) return; // 找出一組解 memset(sat, 0, sizeof(sat)); for (int k=0; k<N+N; ++k) { int i = finish[k]; if (!sat[scc[i]]) { sat[scc[i]] = 1; sat[scc[not(i)]] = 2; } } // 印出一組解 for (int i=1; i<N; ++i) if (sat[scc[i]] == 1) cout << i; else /*if (sat[scc[i]] == 2)*/ cout << "not" << i; }

兩個只能選一個

把or改成xor。留給讀者解決。

UVa 10319 11294 11861 11930 ICPC 3211 3713 4452 4849

三個至少選一個

括號裡面改成三個變數，稱作3-SAT。NP-complete。沒有快速的演算法。

3-SAT被認為是最根本的NP-complete問題。凡是NP-complete問題都可以重新改寫成3-SAT問題，再用3-SAT演算法求解。然而式子繁雜冗長，導致實務上沒有人這麼做。