Lecture 5 迴歸分析- 線性模式與廣義線性模式
5.1 線性模式lm的估計
本節的範例資料檔是餐廳的小費數據 tips.csv,這筆資料有244筆紀錄。 餐廳發現每張帳單的小費,差距頗大。因此想知道,有哪些因素影響了小費額度。資料如圖 5.1
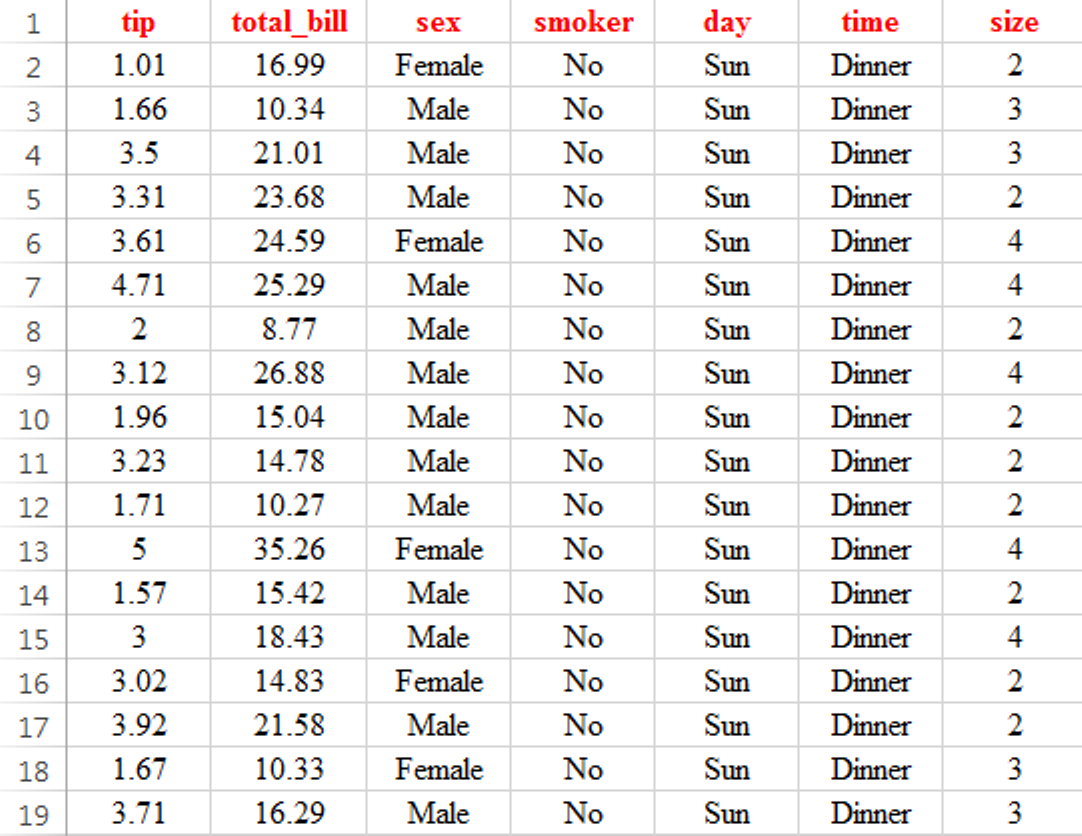
圖 5.1: tips.csv 資料格式
圖 5.1 欄位說明
tip =小費金額,美金
total_bill =帳單金額, 美金
sex = 結帳者性別
smoker=結帳者是否吸煙
day=用餐日
time=用餐時段
size=帳單顧客人頭數(table size)
5.1.1 樣本期望值的代表性問題
在此例中,資料分析人員,提出的問題是:哪些因素和小費金額有關?也就是說,我們以tip做為被解釋變數Y,我們先看看tip這筆資料簡單的敘述統計
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.000 2.000 2.900 2.998 3.562 10.000被解釋變數「小費(tip)」的簡單敘述統計。我們發現244個顧客給的小費,標準差是1.384,約3元的樣本平均數不太有代表性。分量散佈已是這樣,從中位數看,左右很不對稱。
進一步看,由圖 5.2可以看四種重要的資料特性。
首先,次數分佈指出小費集中最高是2元和4元為中的兩個區間。
其次,密度圖的尖峰代表一個集群。2、3、5是三個集中的區塊。也就是說,一個總樣本平均數,不足以代表群體分佈的特點。
第3,盒鬚圖確認了以中位數的集中度,數字具有很大的正偏。且離散度大。
第4,QQ圖繪製資料是否是常態分佈。如果是常態分佈,則散佈點會和理論畫出的那一條直線重疊。如果散佈點的形狀像是S型或是香蕉型,就沒有常態的性質。就此圖來看,距離常態甚遠。也就是說,資料不是對稱,樣本平均數就沒有太大預測的用處。
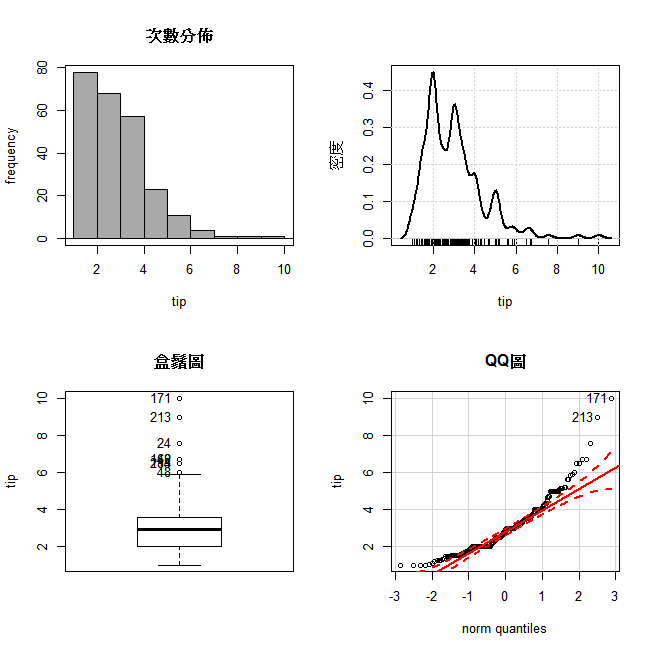
圖 5.2: 小費tips資料的基本特性
因此,綜合來說,樣本期望值不是一個好的資料預測。用它預測,偏誤會很大。
5.1.2 線性迴歸估計條件期望值
並且以total_bill和size做為解釋變數X,欲配適的方程式如下:
\[
tips=a+ b _1 (total\_bill)+b _2(size) +residuals
\]
這一條方程式可以驗證「帳單金額」和「用餐人數」與「小費」關係如何。兩步驟估計上面方程式:
步驟1。選擇變數。如圖 5.3,Target 就是Y也就是方程式左邊的tips。其餘不用的4個分類的類別(Categorical)變數,將之歸為Ignore.
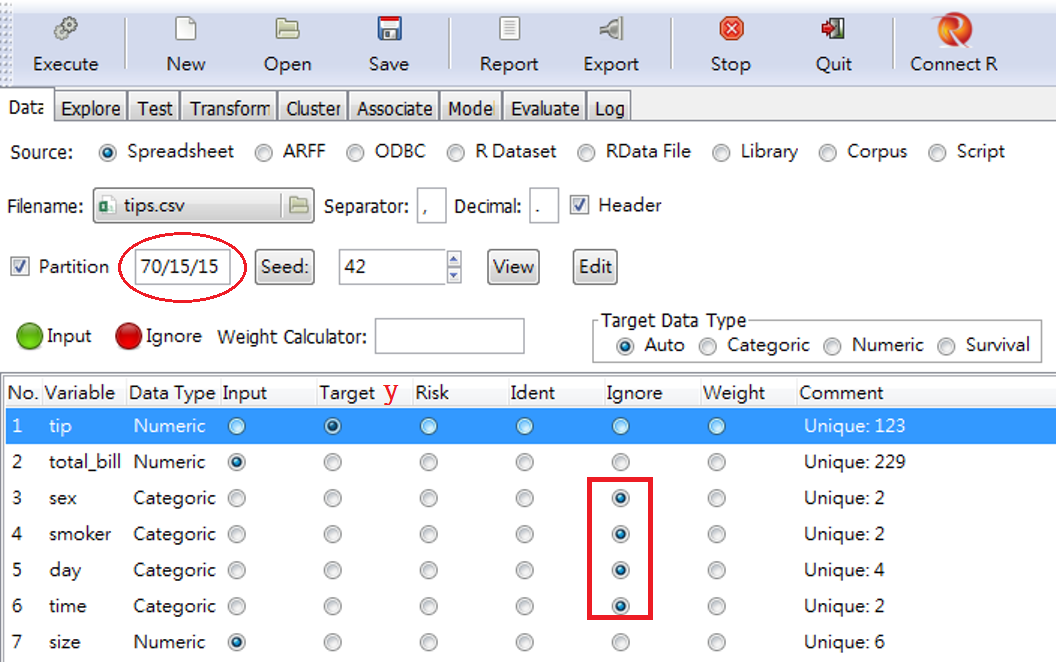
圖 5.3: 選擇變數
圖 5.3 還有一個重要資訊,就是圈起來的 70/15/15,這個是資料探勘的慣用方法:70%來估計,剩下的兩個15%是training/testing sample 比率,這些名詞後面會詳細解說。也就是說,估計的觀察值個數是244*0.7=170。如果需要全樣本,把Partition打勾點掉即可。
步驟2。從主選單選擇倒數第3的Model,進入後再選 lm,如圖 5.4。
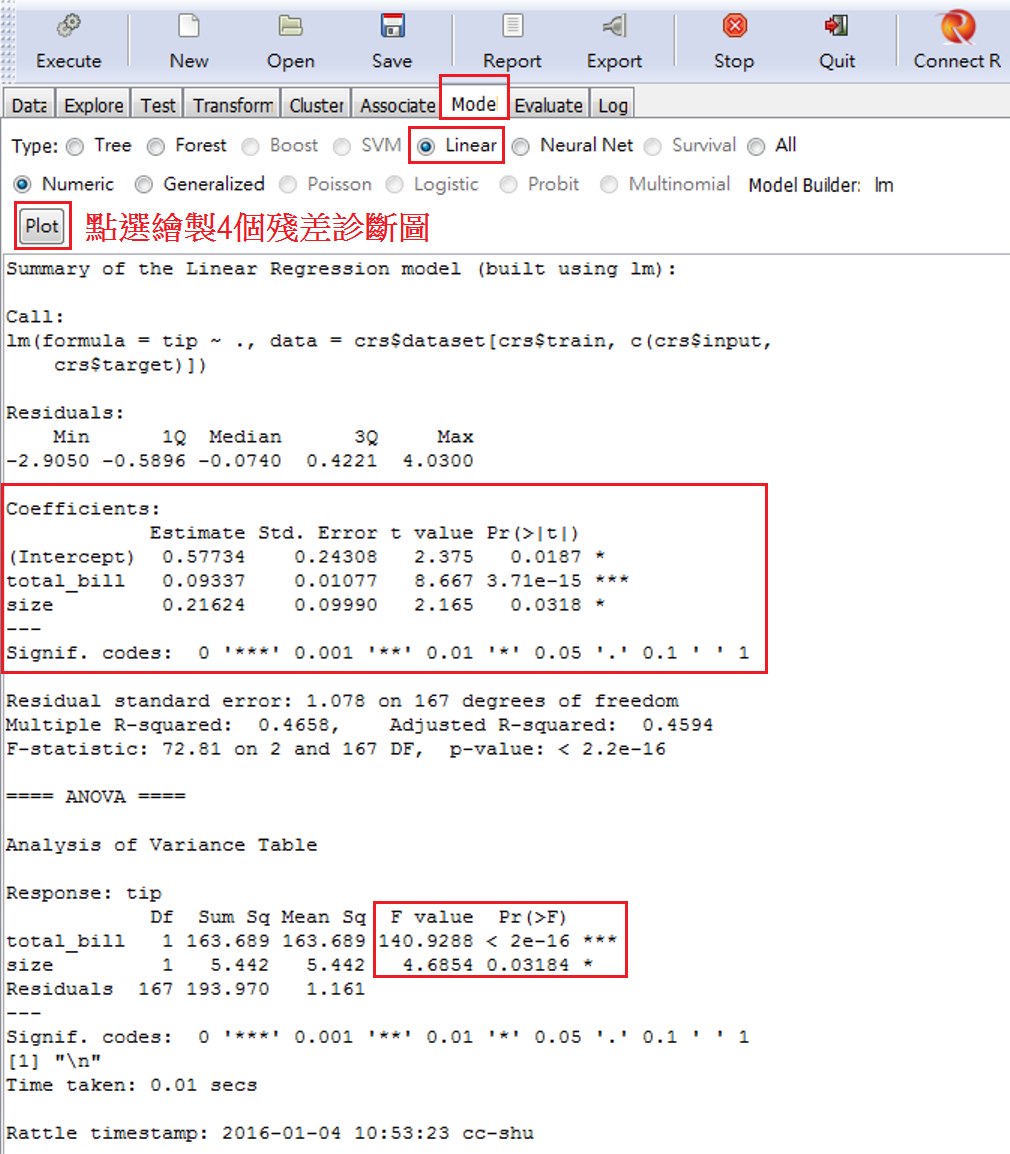
圖 5.4: 估計結果
估計完後,rattle視窗下半部是估計結果。圖 5.4的估計結果, 解讀範例如下:
線性模型的估計結果,在5%顯著水準之下,指出帳單金額和人數與小費金額都呈現正相關。帳單金額越大,人數越多,小費就越高。兩個係數解釋如下:
平均上,當帳單高於平均帳單1單位,小費高於平均小費0.093單位;
平均上,用餐人數多於平均用餐人數 1人,小費高於平均小費0.216單位。
照p-value來看,帳單金額的P-value遠遠小於5%,故顯著性最強。最後,此模型的\(R^2\)約為0.47,所以,200筆小費和平均小費的差異,被兩個變數和個別平均值差異,解釋的程度為47%,另有53%無法被解釋。
上半部就是估計的係數,和配適統計量:R2=0.465以及F統計量=72.81。如圖點選左上方的Plot,就會繪製4個重要的殘差診斷圖,如圖 5.5。
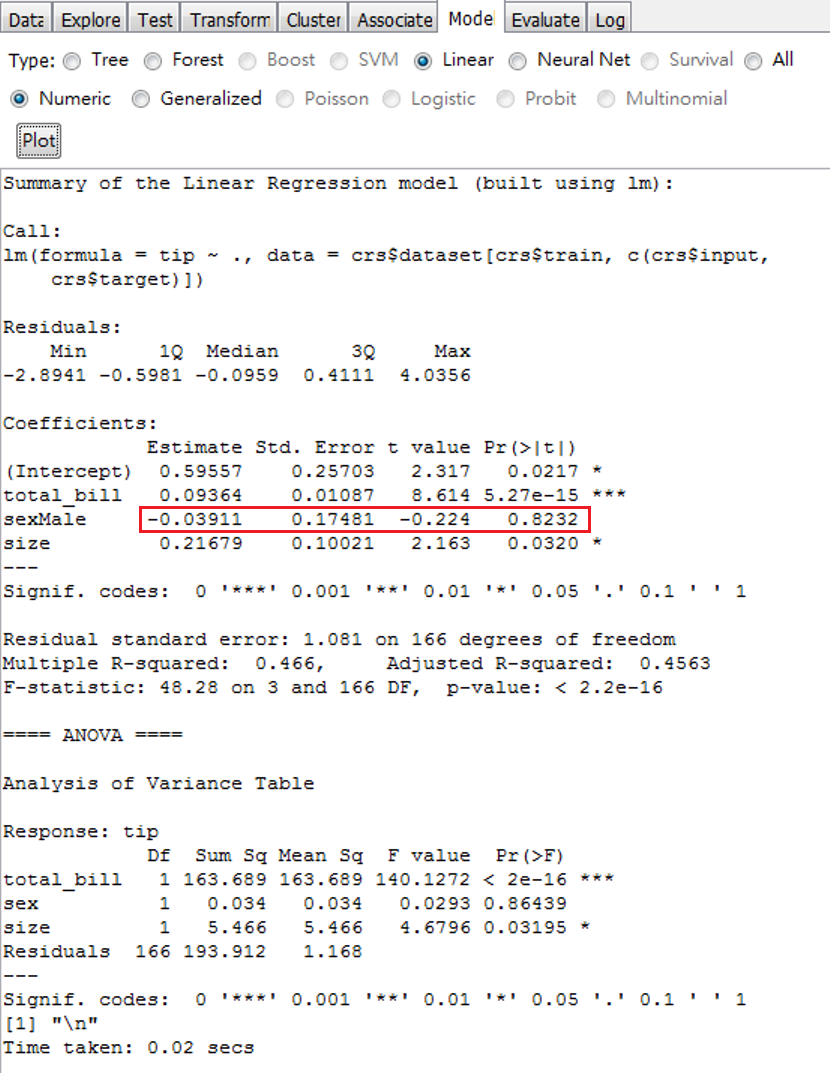
圖 5.5: 殘差診斷圖
圖 5.5的4個殘差診斷圖,必須詳細解讀。我們從左上角順時針一個一個來解釋。
第1個是左上角的「殘差與配適值」散佈圖,一個好的迴歸,這個圖會沒有任何的類型,例如正相關或負相關。圖形中的一條微微凹折的線就是「類型曲線」。好的模型,會和水平線很相近。如果這條類型曲線有明顯的斜率,則代表了模型的設定不完善,可能是有遺漏變數或者非線性關係。
第2個是右上角,診斷殘差是否是常態分佈。如果是常態分佈,則散佈點會和理論畫出的那一條直線重疊。如果散佈點的形狀像是S型或是香蕉型,就沒有常態的性質。線性模型沒有常態其實也沒有很嚴重,如果違反常態,就是顯著性檢定的標準嚴格一點就可以,例如,用1%的水準來看,不用5%。當然,這還要看整體狀況。
第3個左下方的圖是第1個圖的正值版本:將殘差標準化後,取絕對值再開根號。這是用來判斷變異數是否為固定常數(同質變異)的方法。如果是同質變異,則畫出的補助線,會是水平的,如果有趨勢,就不是同質變異。我們的補助線就顯現出正斜率的趨勢。所以,告訴我們有異質變異。
最後一個是右下方Cook’s Distance圖,它將標準化殘差和槓桿(leverage) 值放一起。 圖形右上角的弧形虛線稱為Cook contour,越接近它的點, 對模型有最大的離群影響(outlier influence)。
這個圖形告訴我們,第171個顧客的行為最與眾不同,對模型估計影響最大,同時,他也有著最大的leverage值。
Cook’s distance公式如下:
\[ D_{i}^{2}=\frac{{{\left( \hat{y}-{{{\hat{y}}}_{i}} \right)}^{\prime }}\left( \hat{y}-{{{\hat{y}}}_{i}} \right)}{k{{{\hat{\sigma }}}^{2}}} \]
\(k=\)解釋變數個數。
Cook’s distance計算了每一個樣本點的資訊,圖內的標號是依照Cook’s distance 判斷出來的離群樣本(outliers)。如果原始資料的列名稱有字串,好比人名或地名,則這裡會直接顯示文字。
我們也解釋一下何謂槓桿值?槓桿值也稱為hat 值(hi),定義如下:
\[{{h}_{i}}={{x}_{i}}{{({X}'X)}^{-1}}{{x}_{i}}\]
下標i代表第i個被移除的樣本所計算的值。\(h_i\)這個值的臨界值,學者訂為\(2\frac{k}{N}\),k是解釋變數\(X\)的個數(本例為2),N是總觀察值(本例為244)。觀察值的 \(h_i\) 大於\(2\frac{k}{N}\)(=0.0164)的2倍(0.032)或3倍(0.048),都須要配合其他標準進一步檢視。
5.1.3 當解釋變數有類別變數
我們欲分析的資料,有許多類別變數。因此,我們還想進一步知道「給小費」和這些分類有沒有關係。例如,我們想知道「男女是否有差」?如果我們想知道性別在平均小費的差異時,方程式如下
\[
tips=a+ b _1 (total\_bill)+b_2(size) + b_3(sex) +residuals
\]
步驟1。回到Data頁面,將sex選入,如圖 5.6
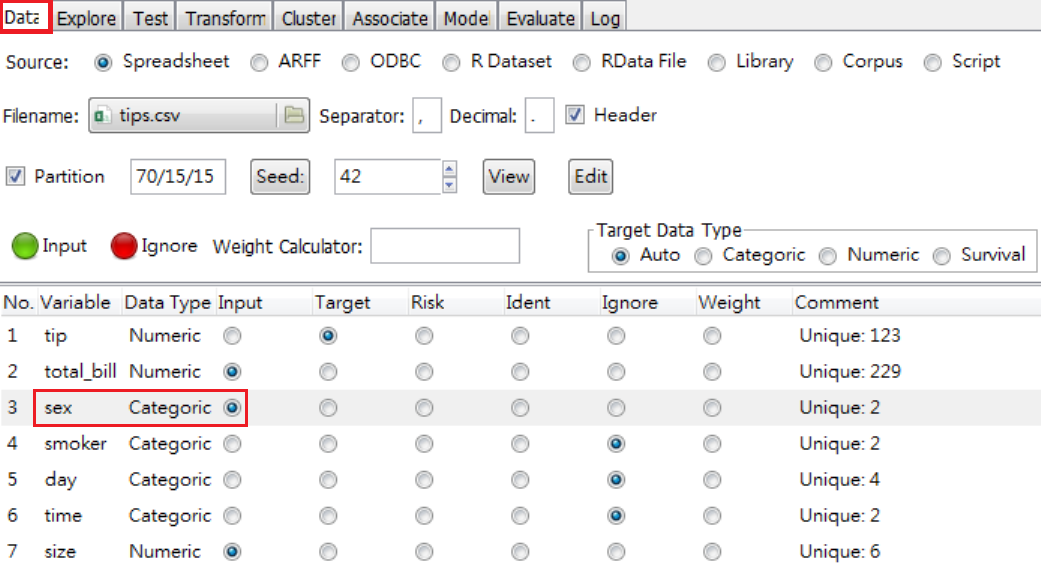
圖 5.6: 操作界面
步驟2。估計,結果如圖 5.7
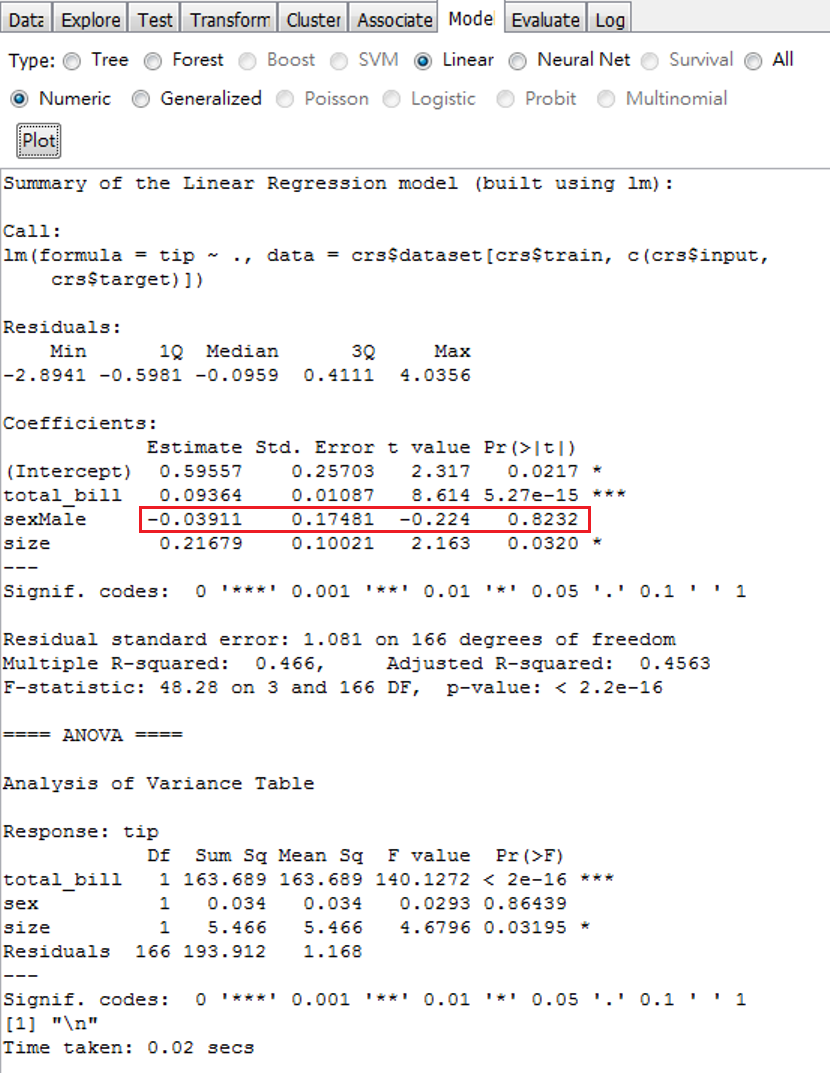
圖 5.7: 增加性別虛擬變數的迴歸結果
圖 5.7下半塊有一個sex[T.Male]的變數,這是R產生一個{0,1}的新變數,代表變數是1時,sex為Male;其餘是0。因為字母排序:{Female, Male}對應{0, 1},所以內建這樣編新變數。這個結果的說明範例,如下:
考慮比較男女對給小費的行為差異,迴歸增加了性別虛擬變數,估計值為-0.039,也就是說,男性給的平均小費比女性要低0.04元美金。但是,P-value為0.82,相當不顯著,所以,結論是:男女性,在給小費這件事,沒有顯著差異。
步驟3。殘差診斷。點選圖 5.7左上方之Plot即可出現,如圖 5.8
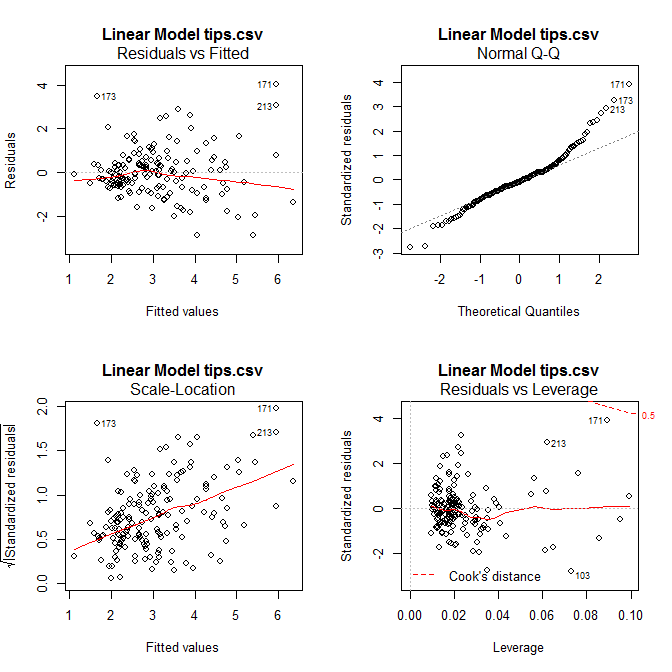
圖 5.8: 殘查診斷
〔練習〕 請比較一週內星期一到星期日(day)的平均小費,有沒有差異?
〔練習〕請問,吸煙的客人比較大方嗎?
在區分吸煙者和不吸煙者的給小費行為,上面的處理方式,是用截距來比較,所以解釋的時候,就著重在樣本平均的差異,也就是吸煙者和不吸煙者的獨立給小費的平均金額。前面兩個練習題,都得出「沒啥差異」的統計結果。
〔練習〕試著同時處理兩個類別變數,看看結果如何解釋。
5.2 廣義線性模型glm
本章用範例資料檔 vote.csv說明廣義線性模式(GLM: generalized linear models),這是2000位美國公民投票行為的資料。資料分析人員,想要知道哪些因素影響了投票行為。這個檔案說明如圖 5.9
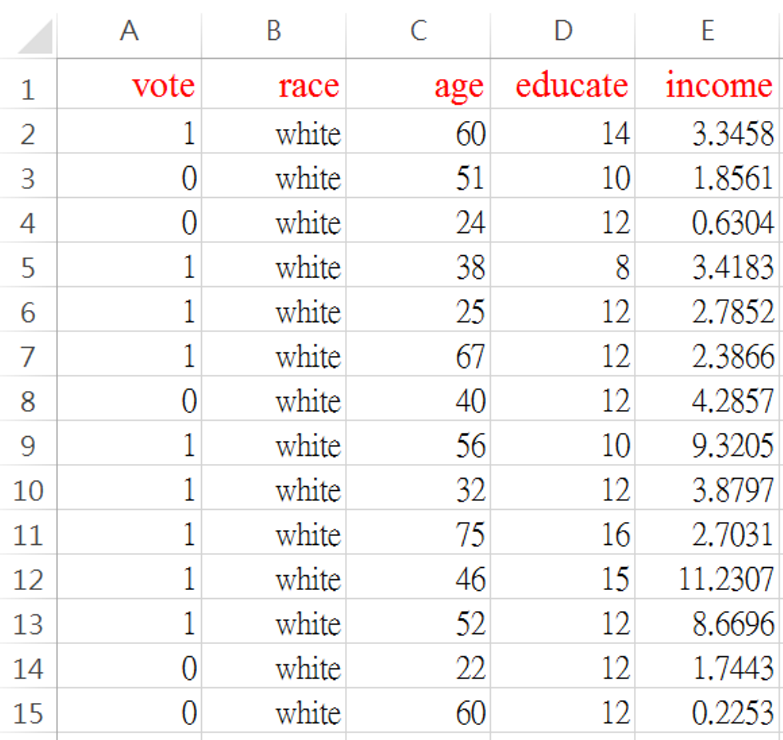
圖 5.9: vote.csv 資料格式
vote =1,有去投票;=0沒有去投票
race =種族別:white=白人;others=其他
age=年齡煙
educate=受教育年數
income=年所得(萬美元)
上面這筆數據的Y是{0, 1},所以一般也稱為選擇問題。 這是研究決策科學常遇 到的數據, {0, 1} 分別代表決策者二分的行為。研究人員,就會想知道什麼因素決定了特定行為的發生。也因為{0, 1}區間的特性,期望值可以解讀為機率。
和上述線性模式不同,稱為線性模式的被解釋變數(或Y),數據是連續資料,也就是實數:正、負和小數都可以。本章要研究的Y是 {0, 1},因此線性模式不適宜配適這樣的資料,因為線性配適線是一條直線,直線的延長會超過{0,1}這個界,如圖 5.10:向右方看,要預測高所得的行為機率,就會大於1;往左方看,低所得的機率就會是負的。雖然,線性機率模型預測大體上還可以,但是對於雙尾極端狀況,就會出現預測問題。
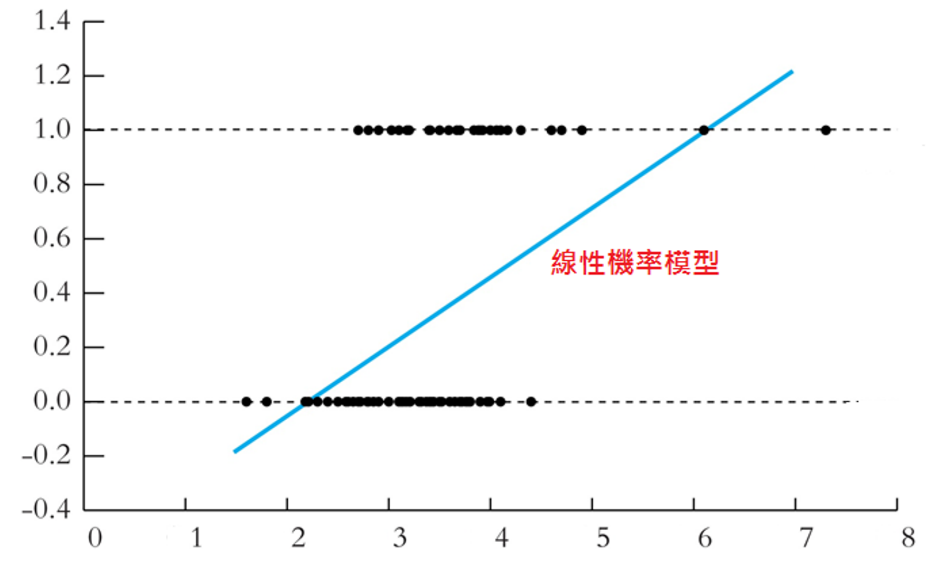
圖 5.10: 線性機率模型
鑑於這種問題,用機率分佈的累積機率密度去配適這樣的資料,應該比較好。也就是圖 5.11。
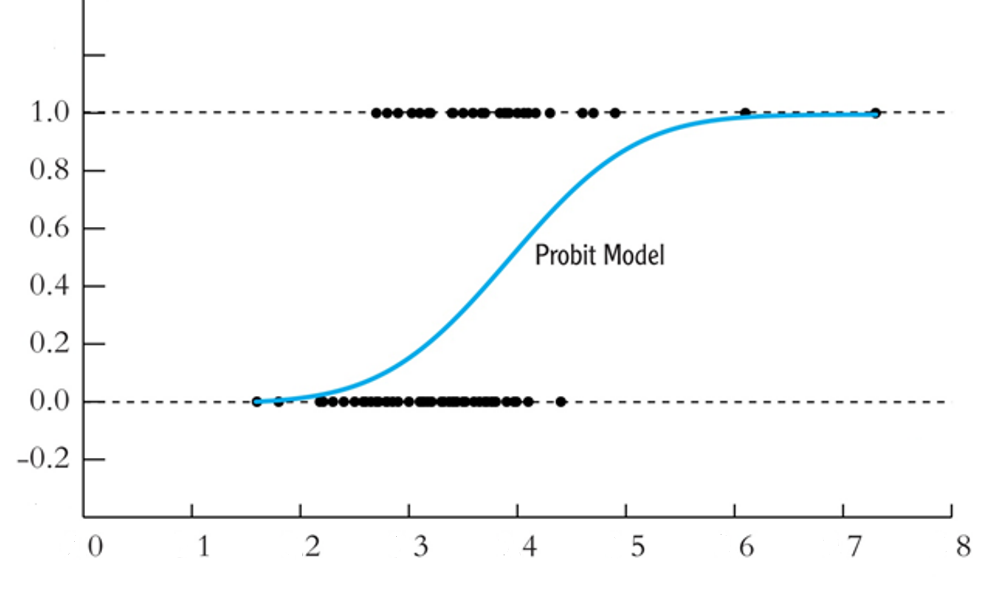
圖 5.11: 機率分佈的累積機率密度
Probit 迴歸利用標準常態分佈的累積機率密度函數 \(\Phi(z)\),估計Y=1 這個事件:也就是,\(z = b_0 + b_1X\)。如下,
\[
Prob(Y=1|X) = \Phi(b_0 + b_1X)
\]
\(\Phi\)是常態分佈的累積密度函數,\(z = b_0 + b_1X\) 稱為 Probit模型的 「z-值」或 「z-指標」。
範例:假設\(b_0 = -2\), \(b_1= 3\), \(X = 0.4\), 所以
\[Prob(Y=1|X=0.4) = \Phi(-2 + 3 \times 0.4)= \Phi(-0.8)\]
Prob(Y = 1|X=0.4) = 標準常態分佈圖,z = -0.8左邊的面積。如圖 5.12,查表就可以知道機率是多少。當然電腦直接就會幫我們計算。
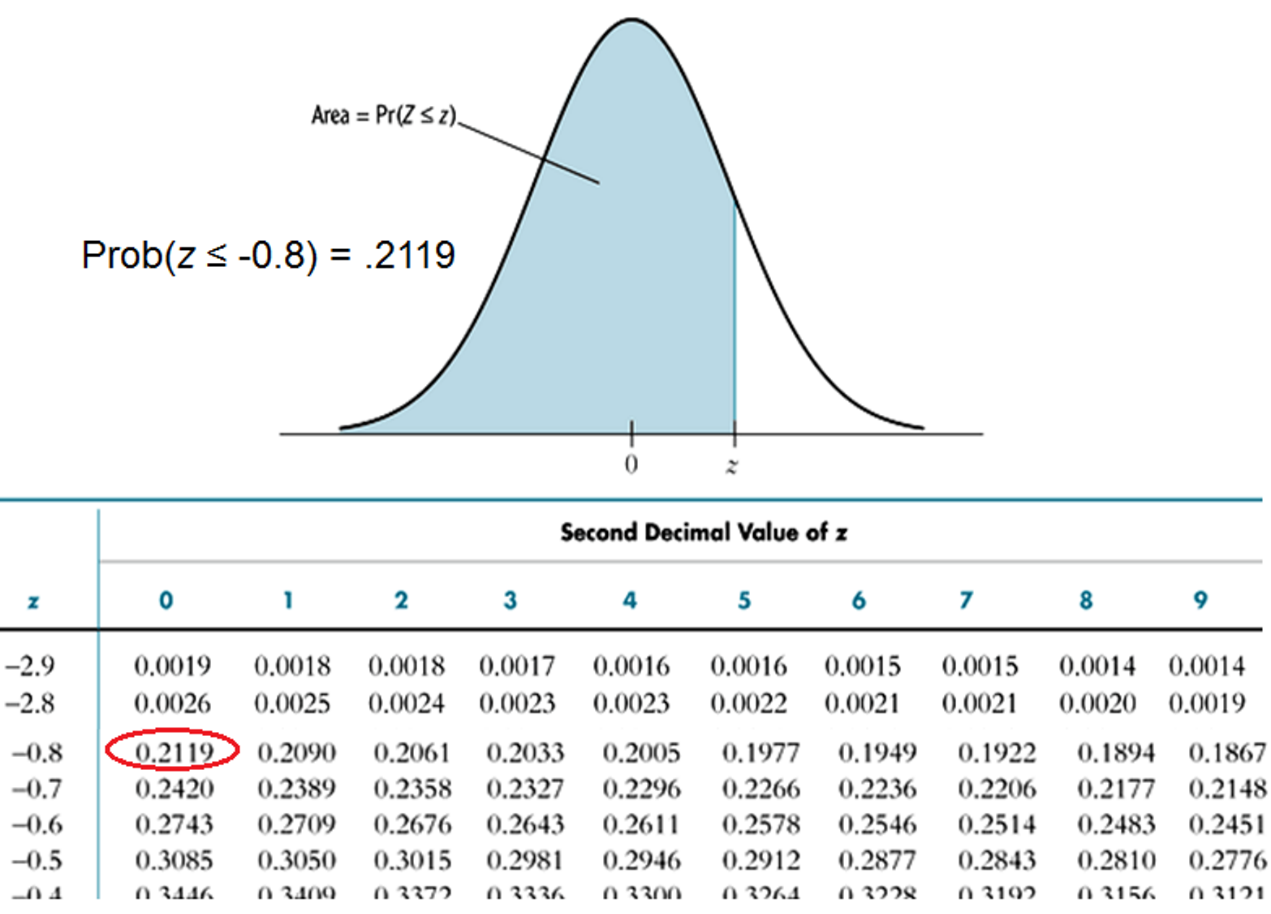
圖 5.12: 標準常態分佈機率
對於二元選擇的Y,Pobit還有一個雙胞胎logit,兩者產生的期望機率大體上是一樣的。Logit函數不連結常態分佈,定義如下
\[
F(b_0+b_1{X})=\frac{1}{1+e^{-(b_0+b_1{X})}}
\]
因為Probit 配適一個機率密度函數,在以前計算很慢,所以開發了logit函數。這個時代計算機的演算能力,都沒問題。我們其實不必太嚴格區分兩者。如這裡所介紹的,GLM的估計原理,須要一個連結函數(linking function)來完成,把z和機率函數連結。要連結哪一個機率密度函數,就要看Y的型態是如何。當Y是測量程度,例如,{不滿意,普通,滿意,很滿意} 這樣的行為時,就不是二元選擇(Binary choice),而是多元排序(Ordered Choice),就要編成{0, 1, 2, 3} ,我們就須要用ordered probit/logit;如果Y是「計數」型,好比某時某地的旅遊人數,連結函數就是將這種「隨機變數的條件期望值」和「機率密度函數」連結的函數,一般「計數」型是布阿松函數,所以就是和布阿松函數連結。
因為機率函數是非線性,所以,這一部份也稱為非線性模型。然而,廣義線性的線性,指的是線性連結函數。綜合來說,GLM有三個重要特徵:殘差結構、線性關係、連接函數。
首先,殘差結構,在線性模式往往用常態去處理。但是,這一章的資料則不是常態,被解釋變數的特徵,會出現高度的偏態,峰態,上下界被限制住一定的區間,以及期望值不可為負。所以,殘差結構往往用隨機變數的家族(family)一詞表示。例如,二項式、布阿松、GAMMA等等。
其次,解釋變數和被解釋變數之間,是一個線性關係。
最後,連結函數就是將線性關係產生Y的期望值,與真正的Y觀察值連結起來的函數。基本上,就是一個轉換。線性期望值可能是一個負的值,但是,真正的觀察值卻必須在0和1之間,因此,就需要再轉換一次,讓它更接近Y所描述的現象。這就是連結函數的功能。
接下來,我們實做三種型態的Y。
5.2.1 二元變數之Probit/Logit GLM
範例資料檔沿用 vote.csv。 我們先研究投票和所得與教育水準的關係。 也就說,我們配適GLM於以下三變數方程式
\[
vote=a+b_1{Age} +b_2{Income}+b_3{Education}
\]
我們先繪製投票與否和所得的線性關係。圖 5.13 指出很明顯的線性問題,而且這筆資料的線性配適還蠻嚴重的。
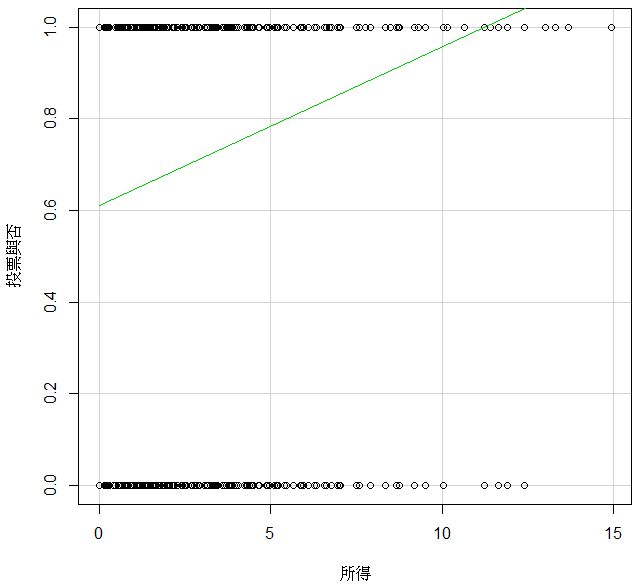
圖 5.13: 投票行為與所得的線性機率模型
rattle的估計,先進入Model,再選Linear,下方會自動依照Target variable的形式,選了Logistic按鈕,如圖 5.14;因為Logistic和Probit是一體兩面的函數,估計時,任一即可。按Execute後,就會產生下半部的報表。依照三個編號解說:
A. Call 就是執行估計的函數,R的函數是glm(),這樣就一目了然。
B. 係數估計值, 這個結果,只能由符號正負作機率增減的解讀,不能解釋成機率增減幅度。例如,三個參數的p-value都很顯著,所以,以Income為例,我們可以從正相關解釋:所得越高,投票的機率越高。不能解釋成:所得增加一單位,投票機率增加0.195。
C. 配適檢定。線性模型的配適度,有一個\(R^2\);廣義線性模型的配適度,其中一個則是Pseudo-\(R^2\) (準\(R^2\))= 0.345,在下方ANOVA上面。
另外,估計結果也回傳一個AIC=1424.6,這個指標越小越好。例如,-200比-150好;但是AIC是比較模型用的,無法用在解讀模型對資料的解釋能力。
除了Pseudo- \(R^2\)還有一個McFadden\(R^2\),定義如下
根據圖 5.14下方兩個值,計算得:1-(1416.6/1591.9)=0.11。
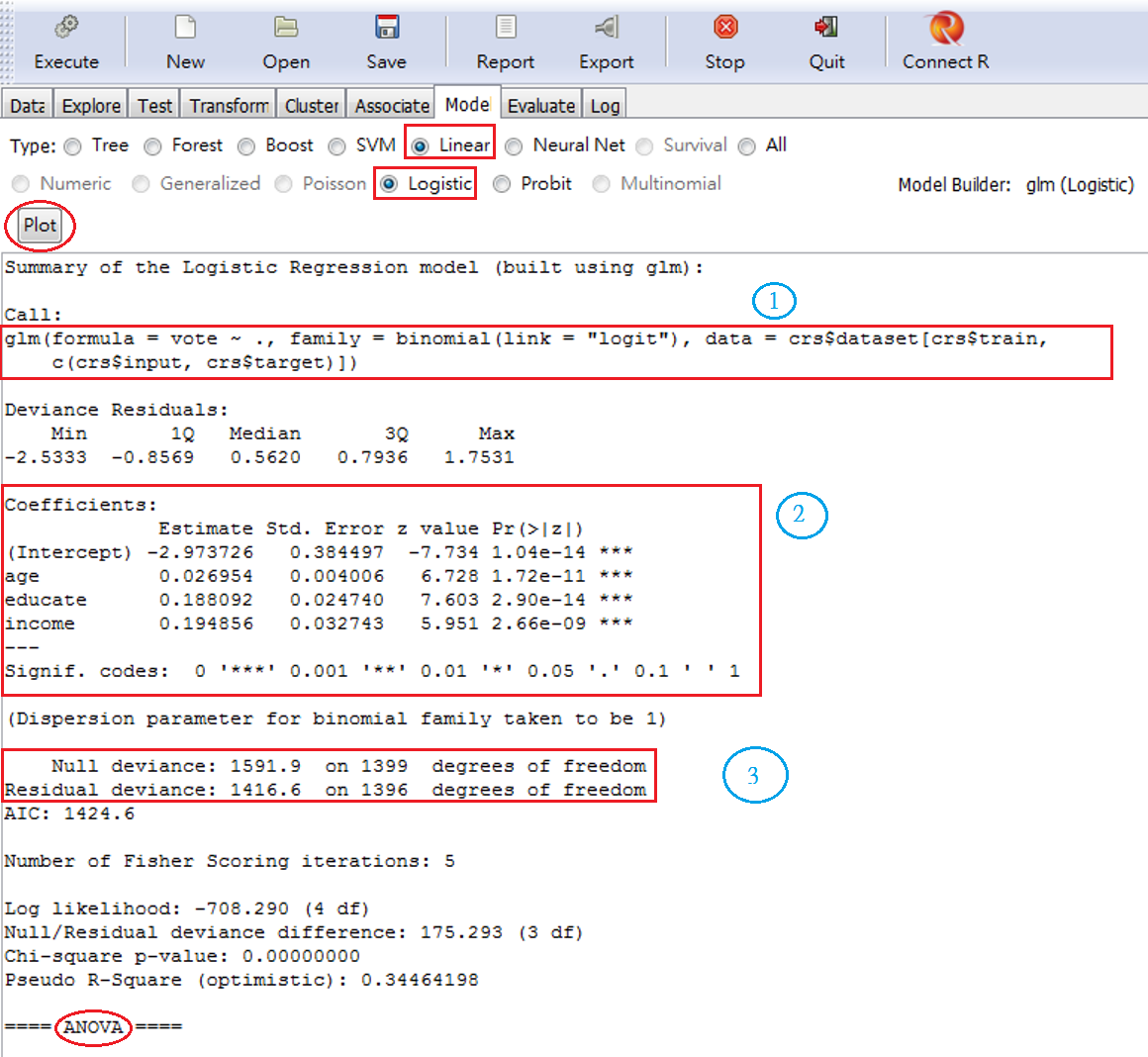
圖 5.14: GLM估計結果
圖 5.14估計結果太長,最下方有一個圈起來的ANOVA部份,實做的讀者請下拉就可以見到,解讀和lm一樣。
最後,和lm一樣的殘差診斷圖,按左上方的Plot就可以產生如圖 5.15配適度解讀,和lm一樣。機率模型配適logistic的結果,和常態相距甚遠。
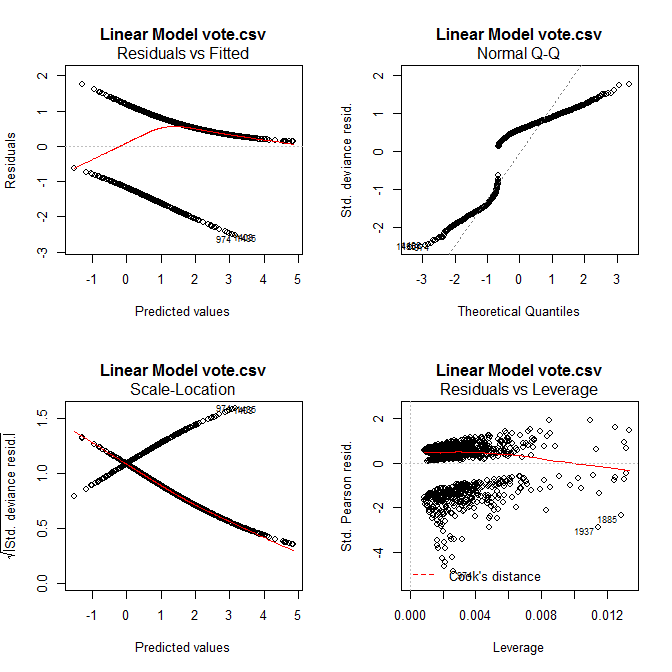
圖 5.15: 殘差診斷
〔練習〕估計上述模型,選用Probit看看結果如何。
〔練習〕這筆資料有一個類別變數race:白人與非白人。請增加這個變數,看看種族類別是否與投票行為有關?
再來就是 over-dispersion 和參數變異數修正。 理論上,GLM架構的殘差最適表現是卡方分佈。但是,實際上會出現較大的殘差變異,這就稱為over-dispersion。由圖 5.14,Pseudo- \(R^2\)上方的 \(\text{Chi-square p-value} \sim 0.00000000\), 拒絕了殘差是卡方分佈的虛無假設。 如果我們模型的解釋變數都是正確的,但是出現這種狀況時,可能的原因是數值刻度沒有適當轉換,或者函數的結構形式不正確。
所以,我們需要修正。處理這種問題的方法,就是先計算 over-dispersion數值,就是殘差平方和除以自由度,也就是模型的變異數。再用這個數值去修正原來的估計結果。這樣做,必須用到主控台的語法,分步驟解釋如下:
步驟1。複製 Call 下方的方程式,將其增加定義為 GLM1,如下:
GLM1<-glm(formula = vote ~ ., family = binomial(link = “logit”), data = crs\(dataset[crs\)train, c(crs\(input, crs\)target)])
步驟2。計算 over-dispersion。
估計物件名稱是GLM.1,分子是sum(residuals(GLM.1)^2),分母自由度是GLM.1$df.res,故我們定義over-dispersion參數如下
其實這個數字在輸出表中已經有了,就是最下方residual deviance 2027.9,自由度是1996。
步驟3。計算成功之後,我們重新執行下列指令。
這3個步驟利用主控台的Command Line,如圖 5.16。
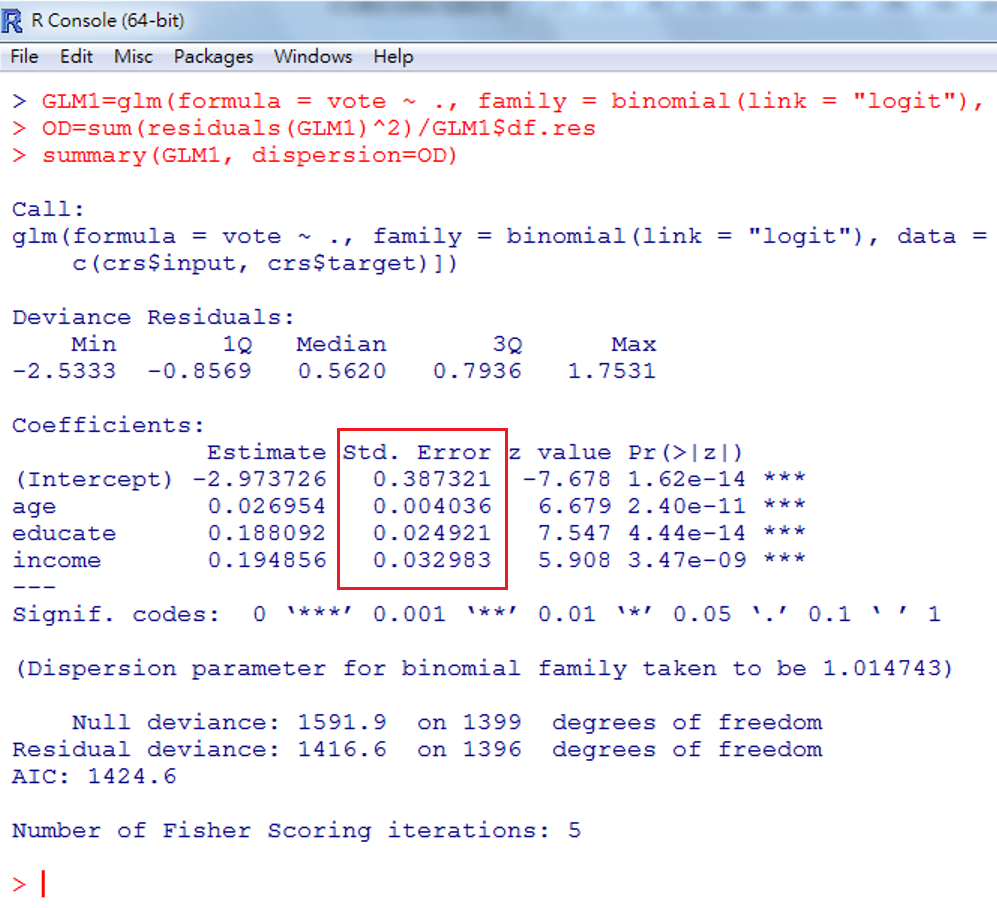
圖 5.16: 基於 over-dispersion 修正的穩健標準差
5.2.2 計數型變數之Poisson GLM
本節的範例資料檔用countStrike.csv,這筆資料欲研究罷工次數的影響因素。這筆資料變數的說明如下圖 5.17。
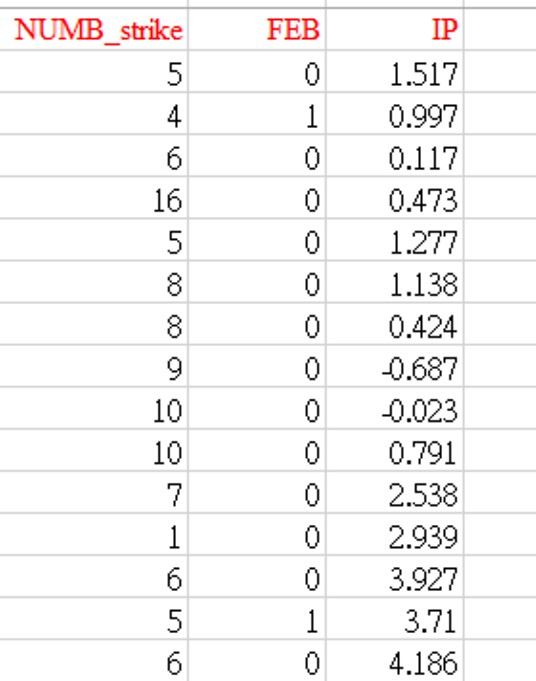
圖 5.17: countStrike.csv
Numb_strike: 罷工次數
Feb: =1, 發生在二月;0=其他月份
IP:以工業生產指數變動率計算的經濟成長,%
載入後,記得調整Target variable,我們的Target variable是Numb_strike。估計這種隨機變數,模型是布阿松。三個連結函數只是轉換成機率時用的函數,結果會有些許差異,但是增減方向不變。圖 5.18下半部是估計結果,說明範例如下:
發生罷工次數的時間,二月比其他月份的平均次數要少;經濟成長率較高,平均罷工次數也較高。
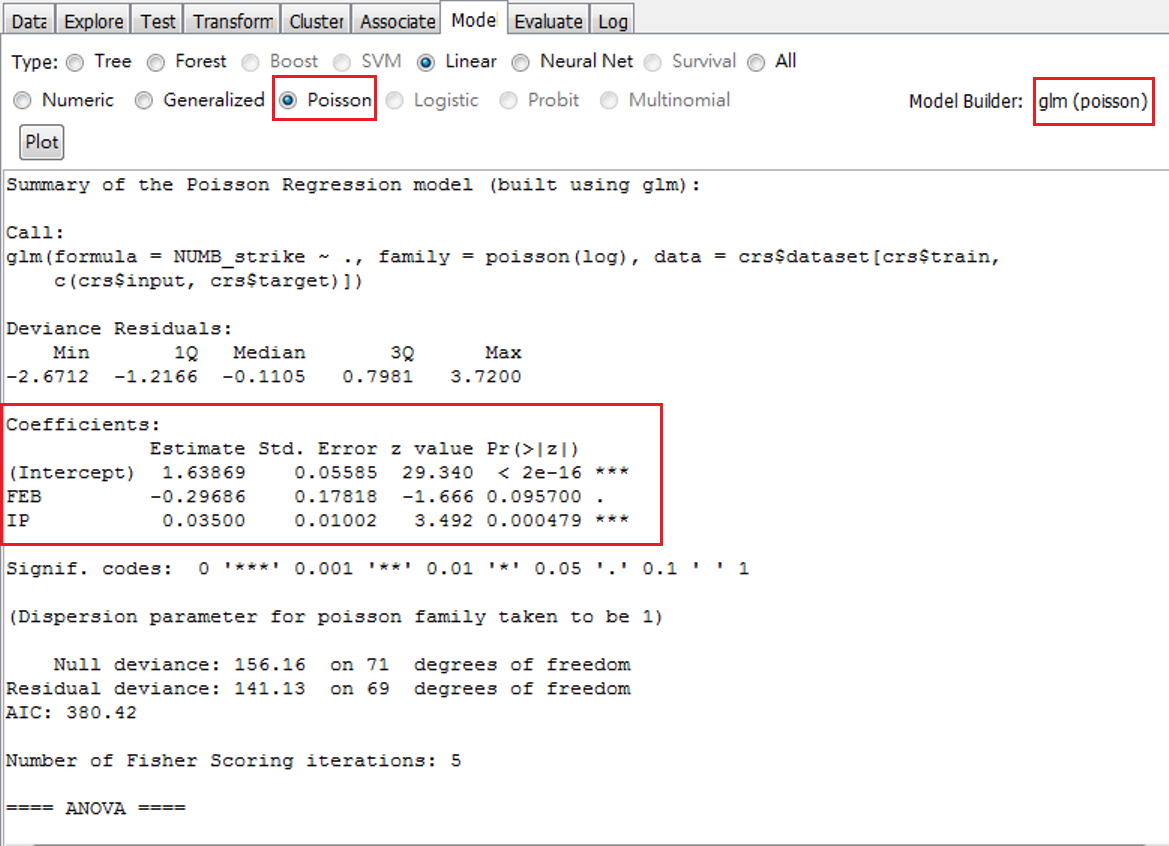
圖 5.18: 估計結果
按左上方的Plot就會畫出如圖 5.19的4個殘差診斷圖。
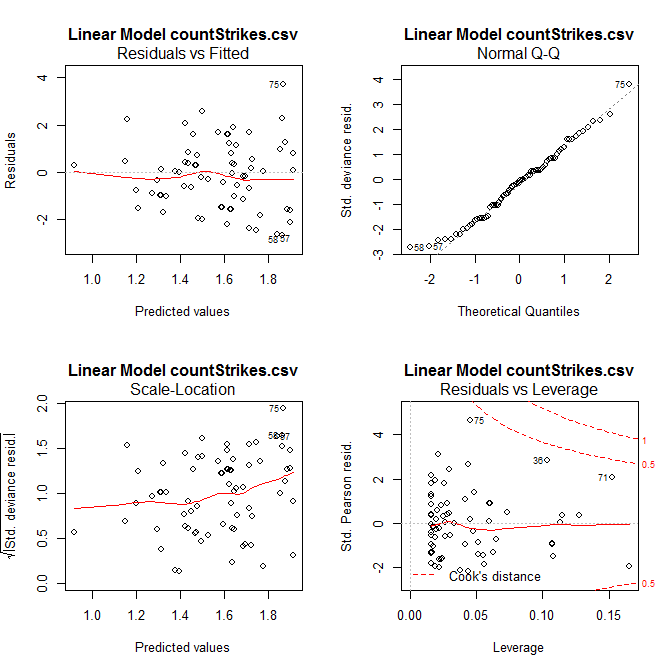
圖 5.19: 布阿松之殘差診斷圖
〔練習〕用fitted() 比較三個連結函數預測的平均罷工次數,差異如何。
〔練習〕請計算Over-dispersion,並修正原估計結果。
〔練習〕解讀圖 5.19的殘差診斷圖
5.2.3 多元選擇 GLM— Multinomial Probit/Logit
二元選擇的問題,行為者的選擇是二選一。一個更普遍的情況是行為者是從多個選項中選擇一個。例如,圖 5.20 健康保險資料mlogit.csv的欄位變數。
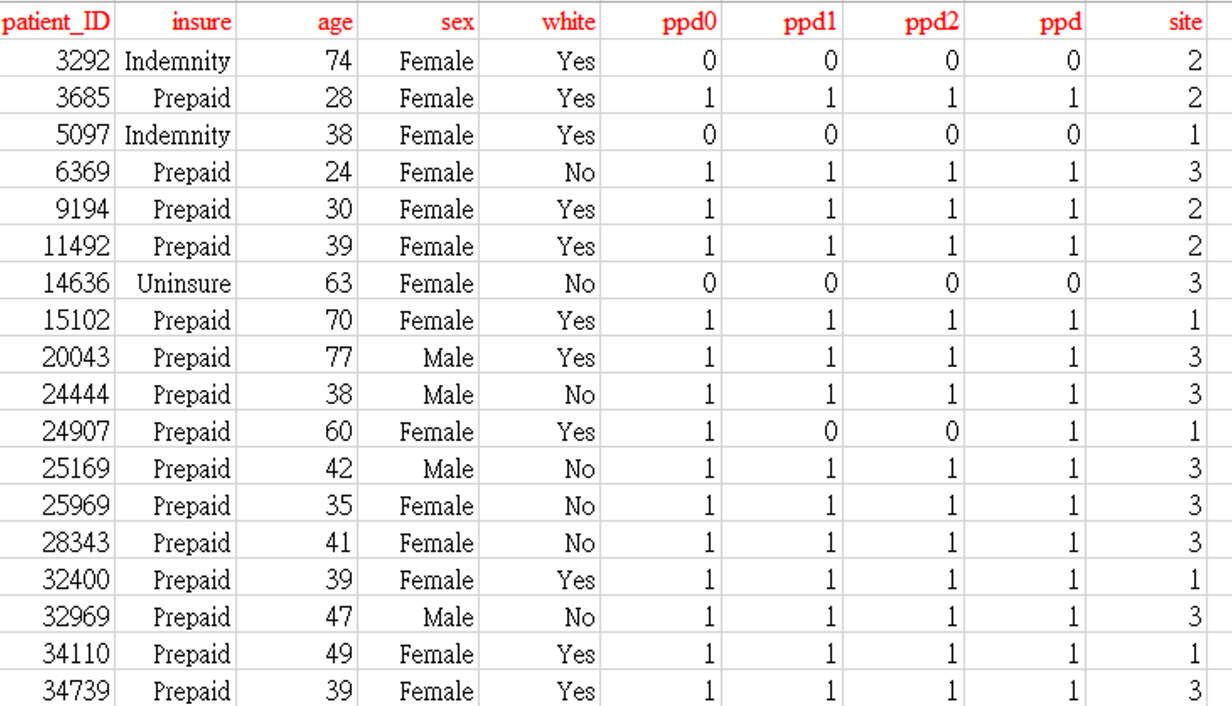
圖 5.20: 資料mlogit.csv
Insure 是我們的被解釋變數,有三項:
indemnity: 保險損害賠償。
prepaid: 預付計畫,如HMO(health maintenance organization 維護健康組織)的計畫。預付一筆費用,就可以無限使用。
Uninsure: 沒有保險
其他欄位代表:
Sex: 性別
White: 是否為白人
ppd0: prepaid at baseline
ppd1: prepaid at year 1
ppd2: prepaid at year 2
這筆資料用來研究病人對於方案的選擇和人口因素的關連。類似資料研究的問題,教育方面有大學生畢業後的選擇:碩士、就業、留學。載入資料後,以insure為Target variable,我們配適年齡(age)、性別(sex)和種族(White)三個變數。如圖 5.21執行,rattle依照Target variable的屬性,會選擇適當的函數。
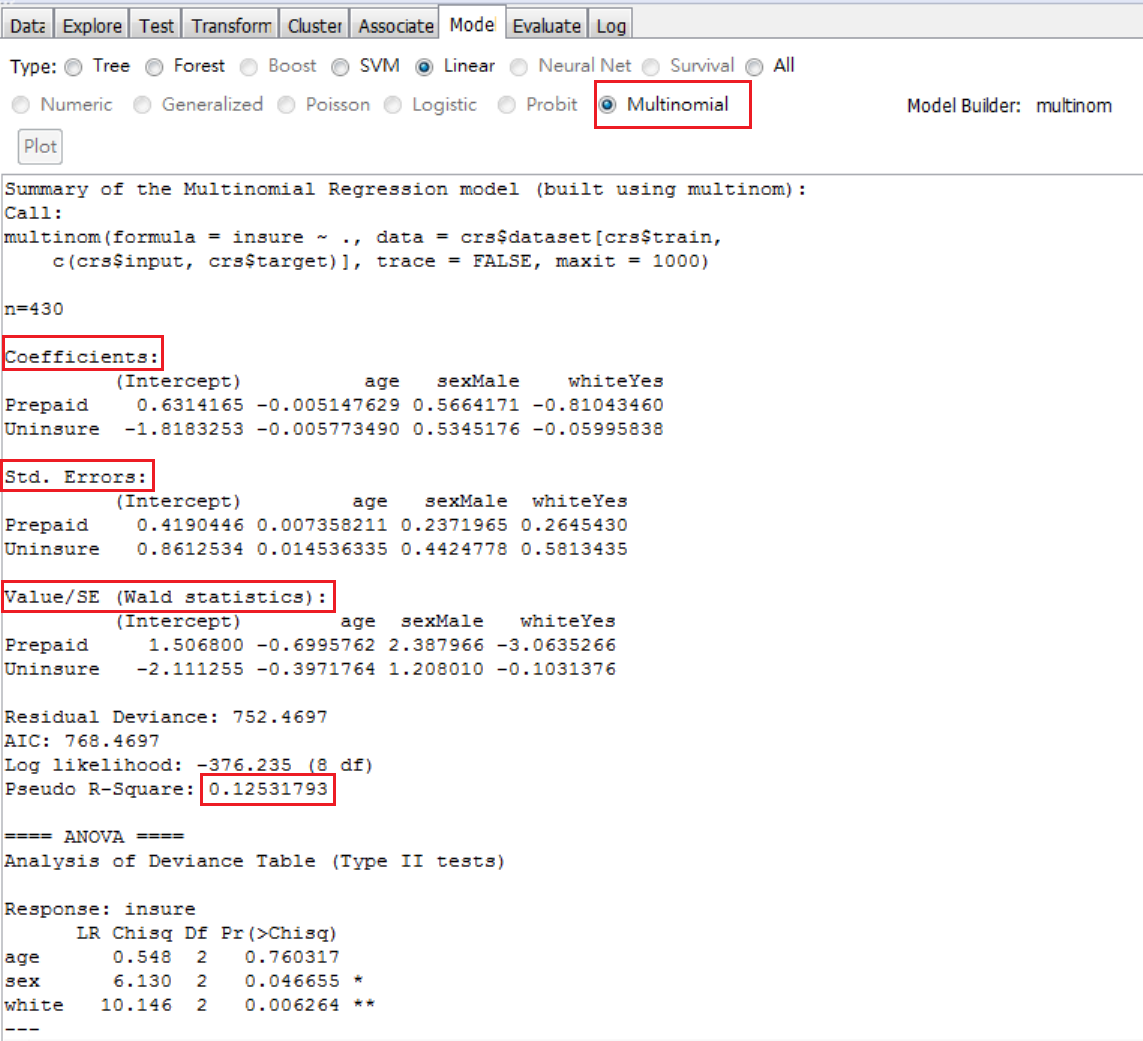
圖 5.21: 估計結果
最後是如圖 5.21的視窗,這估計方法,會將Target variable三個分類項目中的一個,視為base,R裡面是自動取字母排在前面的,就是indemnity。base的項目,就是和其他兩個比較的。所以,這結果的解讀,必須小心。下半部估計結果,R對結果的輸出,是依照估計項目去分3部份:Coefficients(係數),Std. Errors (標準差)和 Value/SE (顯著性檢定統計量)。以係數為例的解讀如下:
第1. 截距代表了三個變數的觀察值是0時的機率,計算方式,在主控台視窗,執行兩行語法
cc=c(0, 0.6314, -1.8183)
exp(cc)/sum(exp(cc))
利用主控台視窗執行,非常簡易,如圖 5.22
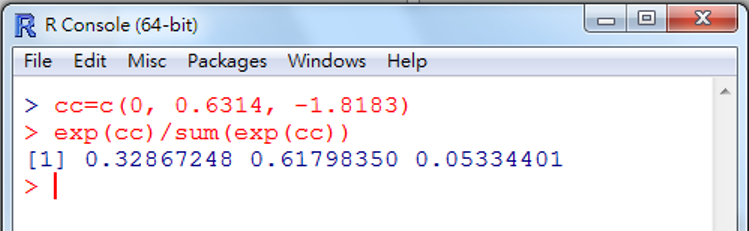
圖 5.22: 利用主控台Console計算個別機率
第1行定義三個數值:0就是base項,也就是indemnity;另外兩個數值就是Prepaid和Uninsure項的截距參數。第2行計算個別機率,得到下面結果
## [1] 0.32867248 0.61798350 0.05334401
當三個變數的觀察值是0時(女性且非白人),個人選擇indemnity的機率是0.32,選擇prepaid的機率是0.617,選擇不保險的機率是0.053。
第2. 斜率代表了log-odds機率,測量了1個人從選擇baseline(=indemnity),過渡到選擇prepaid或選擇uninsured的機率。例如,age斜率-0.0051
cc=c(0, -0.0051, -0.0058)
exp(cc)/sum(exp(cc))
## [1] 0.3345455 0.3328437 0.3326108
三者機率類似:意思是說,年齡增加1歲,從「選擇baseline (=indemnity)」,過渡到「選擇prepaid」的機率是0.33284。