Lecture 3 資料性質檢定與轉換
rattle資料分析依選單的設計,下一步是資料性質檢定。在rattle架構,可以檢定分佈、平均數、變異數和相關係數顯著與否。為解釋這項功能,我們載入銀行薪資bank_wage.csv的資料。
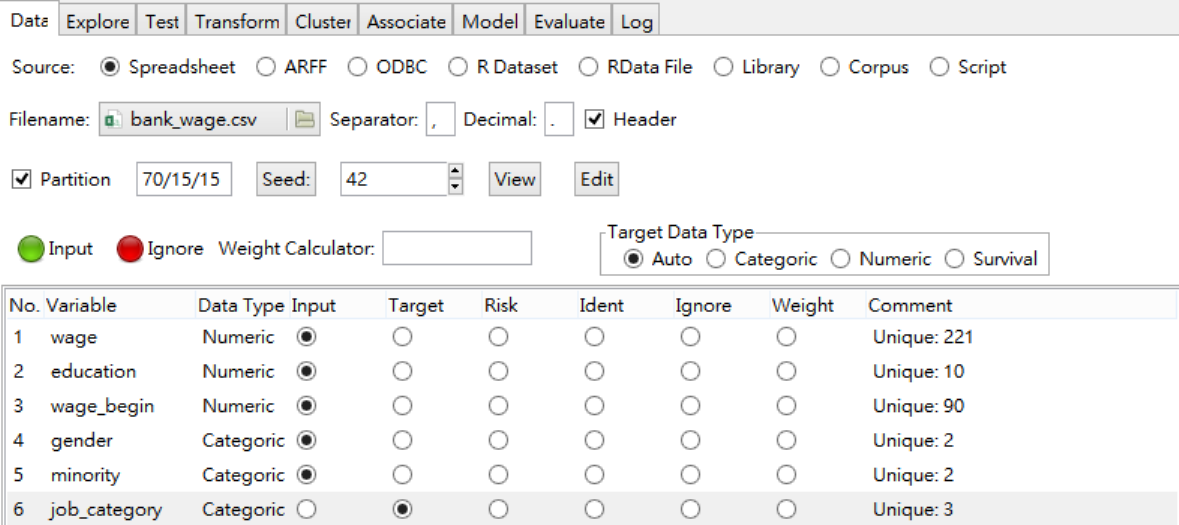
圖 3.1: 載入bank_wage 數據
圖 3.1 的資料說明如下:
wage: 目前薪資
education: 所受教育年數
wage_begin: 入行起薪
gender: 性別。Female/Male
minority: 是否是少數民族?Yes/No
job_category: 工作類別
載入資料後,我們切換至Test的選項。rattle下半部,有對這些函數做簡易解說,如圖 3.2
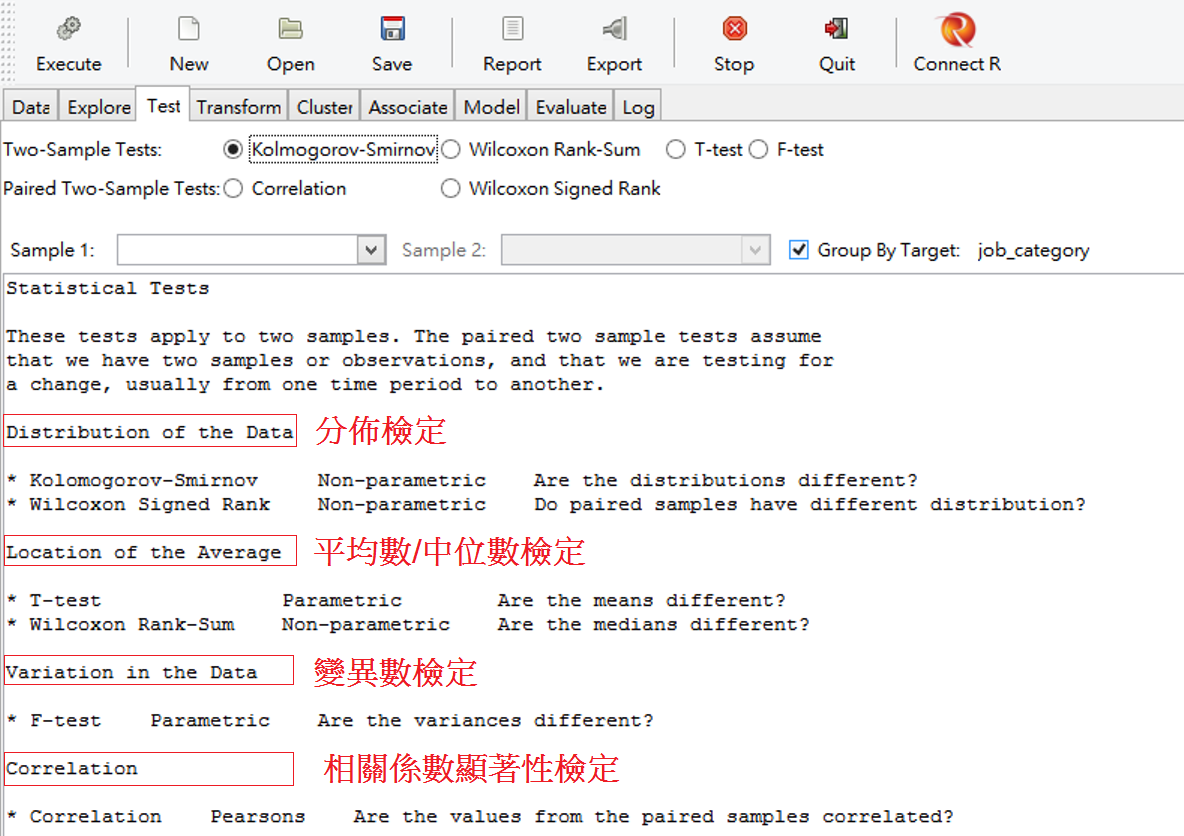
圖 3.2: 檢定介面據
圖 3.2 的介面解說有2個重點:
A. 成對樣本4個檢定:分佈、平均數/中位數、變異數和相關係數。本章依序分4節解說實做。
B. 分群檢定是依照Data中選的Target 變數。因為是成對樣本(paired sample)檢定,所以檢定的功能只限於2組,內定選擇的job_category內分類,有3個level。這邊僅選擇前2個。
3.1 獨立變數之雙樣本檢定
所謂的獨立樣本(Independence sample)檢定,是指有一筆資料,如員工薪資;有兩個分類,例如男女,為彼此獨立互斥的抽樣單位,故名獨立樣本。我們要檢定兩個分類樣本的性質是否一樣,例如,男性員工薪資和女性員工的平均薪資,是否相等。以下依照軟體項目依序介紹。
開始之前,我們先將Target變數,改成gender性別。
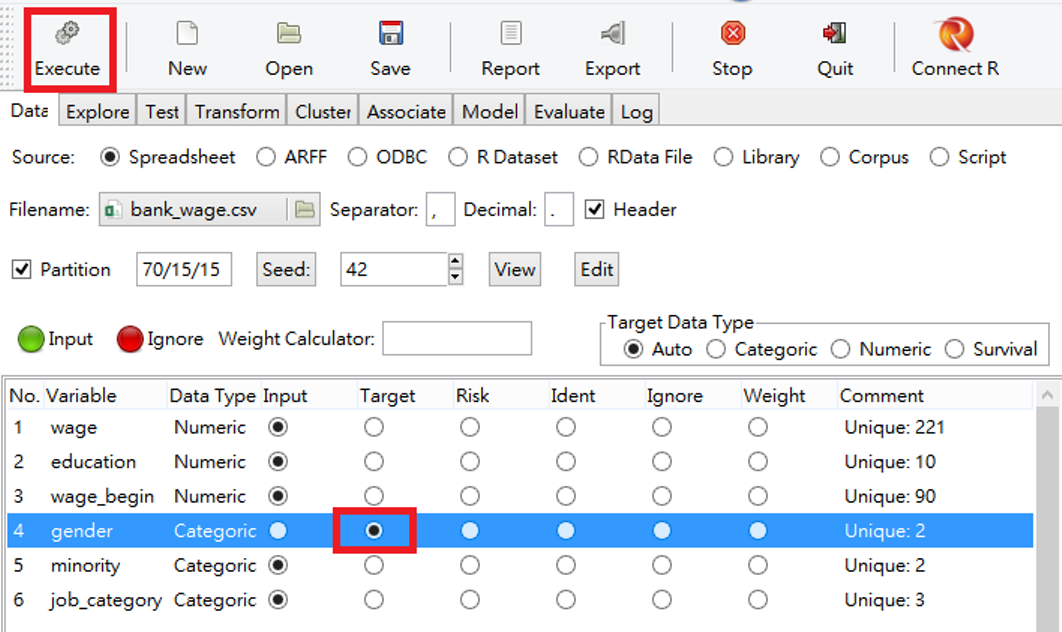
圖 3.3: 切換Target 為gender
3.1.1 Kolmogorov-Smirnov test
H0: 一筆資料,在兩種分類的樣本,其分佈是一樣的
這種檢定是無母數(Non-parametric)檢定。就是說,這兩種檢定都不預設母體分佈,也不去檢定樣本是否是來自某種特定的母體。
Kolmogorov-Smirnov 統計量檢定的虛無假設是:兩筆資料來自相同分佈,有雙尾檢定量和兩個單尾檢定量。Kolmogorov-Smirnov 統計量也稱為 D 統計量。 如果兩筆樣本資料類似,此統計量收斂至0。 按Execute後,結果如下:
##
## Asymptotic two-sample Kolmogorov-Smirnov test
##
## data: wage_begin by gender
## D = 0.64696, p-value < 2.2e-16
## alternative hypothesis: two-sided上面的結果有2點解說。
1. 根據P VALUE,類似分佈的虛無假設,是被顯著拒絕的。也就是此處結果可以解讀為:’Male’和’Female’員工起薪(wage_begin)的分佈是不一樣的。
2.根據P VALUE的Alternative(對立假設)中,比較能接受虛無假設的是兩群資料的差異小於0 (Alternative Less),顯著拒絕的是大於0(Alternative Greater)。這樣使的雙尾檢定也相當顯著。基本上是右尾支配了整個結果。
3.1.2 Wilcoxon’s rank-sum test
H0: 兩筆資料中位數是一樣的
Wilcoxon’s rank-sum test針對一筆變數,群組變數「只有兩個」類別。如下檢定結果,拒絕男女起薪相等的虛無假設。無母數檢定,不是由平均數去推論。所以,虛無假設必須寫成:男女起薪中位數相等。結果如下:
##
## Wilcoxon rank sum test with continuity correction
##
## data: wage_begin by gender
## W = 7854, p-value < 2.2e-16
## alternative hypothesis: true location shift is not equal to 03.1.3 T-test
一般這也稱為獨立樣本t檢定。
H0: 兩筆資料的平均數相等
這個虛無假設一般也等同兩個平均數相減為0。這個檢定臨界值的判斷,假設虛無假設正確時的機率分佈是常態分佈。因此,萬一不是常態分佈,則使用前述無母數的檢定量 Wilcoxon Rank-Sum test。
rattle執行的T檢定,除了平均數相等,也檢定了變異數相等。結果如下:
##
## Welch Two Sample t-test
##
## data: wage_begin by gender
## t = -11.987, df = 318.82, p-value < 2.2e-16
## alternative hypothesis: true difference in means between group Female and group Male is not equal to 0
## 95 percent confidence interval:
## -8392.667 -6026.188
## sample estimates:
## mean in group Female mean in group Male
## 13091.97 20301.40以上,有幾個重點必須說明。
結果內的性別分組對應的是女性和男性,因為分組變數是文字,會依照字母排序。女性Female的F,比男性 Male的M排在前面。
sample estimates 計算了表內的x 和y對應組的平均數和變異數。
t= -11.9875 檢定 H0:女生平均薪資-男生平均薪資=0
顯著地用男性薪資大於女性薪資,拒絕兩者相等的虛無假設。
3.1.4 F-test
H0: 兩個樣本的變異數相等 由bank_wage這筆資料為例,因為性別是男女兩個分類,我們檢定起薪(wage_begin)這筆資料,男性和女性兩個樣本的變異數是相等的。虛無假設如下: H0:女性起薪的變異數=男性起薪的變異數
這個檢定是用來檢視男女員工的薪資,和組內平均薪資的差距(Deviation)是否一樣。和T-test不同之處在於這是用變異數比率來檢定,也就是女性變異數放分子,男性變異數放分母,兩者相除的比率,在虛無假設之下是1。
##
## F test to compare two variances
##
## data: wage_begin by gender
## F = 0.1038, num df = 215, denom df = 257, p-value < 2.2e-16
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
## 0.08040836 0.13438901
## sample estimates:
## ratio of variances
## 0.1037975以上的SAMPLE ESTIMATE為0.1038,統計量F也是0.1038,P VALUE極小,也就是說,兩者不等且顯著地小於1。
檢定結果,報表解說範例如下:
依據F統計量的檢定「男女起薪的變異數相等」,p值遠小於 \(10^{-16}\),因此顯著地拒絕「男女起薪的變異數相等」的虛無假設。
3.2 關聯樣本關係檢定
所謂關聯樣本(dependence sample) tests,是指有2筆樣本資料變數,檢定他們的關聯性質。用這個關聯名稱,是因為兩筆資料,例如wage和wage_begin,都是同一個人,所以是同一個樣本單位,故名。接下來兩個例子,就是用這兩筆資料。
3.2.1 Correlation相關性檢定
H0: 兩個變數的Pearsons相關係數是顯著的
這個虛無假設,就是檢定「Pearsons相關係數=0」
##
## Pearson's product-moment correlation
##
## data: dat$wage_begin and dat$wage
## t = 40.276, df = 472, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.8580696 0.8989267
## sample estimates:
## cor
## 0.8801175計算的相關係數是0.8801,t 值是40.28,顯著拒絕虛無假設。
檢定結果,報表解說範例如下:
依據Pearson’s Correlation Test統計量的檢定,p值遠小於 \(10^{-16}\) ,因此顯著地拒絕「銀行員工起薪和當前薪資無關」的虛無假設。
3.2.2 Wilcoxon sign-rank test
這是成對樣本的Wilcoxon sign-rank檢定,也稱為Mann-Whitney test,因為在同一時間,這兩群學者,同時提出一樣的檢定量,不同軟體有不同名稱,我們知道即可。這個檢定,比較兩筆相關變數是否相等,不需要分組變數。類同「成對依賴樣本 t 檢定」,建立在兩筆資料相減後符號(sign)的排序(rank)。
##
## Wilcoxon signed rank test with continuity correction
##
## data: dat$wage and dat$wage_begin
## V = 112575, p-value < 2.2e-16
## alternative hypothesis: true location shift is not equal to 0如上,統計量V=112575,計算的p-value極小,可以顯著地拒絕虛無假設。
檢定結果,報表解說範例如下:
依據Wilcoxon sign-rank統計量的檢定,p值遠小於\(10^{-16}\),因此顯著地拒絕「銀行員工起薪和當前薪資相同」的虛無假設。
3.3 資料轉換 Transform
資料分析往往須要對資料做一些數值上的轉換或處理,例如,資料差距過大或具有非線性時,取對數是一個方法,但是,對數函數必須對非0正數才可以。原始資料有缺值時,我們一則移除(omit),一則插補(impute)。移除簡單,插補就有插補值的計算原則。除此,還有標準化等等,這些我們統稱數據轉換(transform)。rattle內有許多轉換函數。本節練習檔使用模擬產生的數據檔na_value.csv,載入後如圖 3.4 ,前五筆數據有缺值(missing),第6筆沒有缺值,皆是大於0實數。
資料轉換的類型(Type)有四種:Rescale(尺度比例重新調整),Impute(插補),Recode(重新編碼),Cleanup(清理資料),點選每一種轉換類型,就會帶出可以執行的函數。如圖 3.7 至圖 3.10 圖樣的顯示,就很清楚的說明。
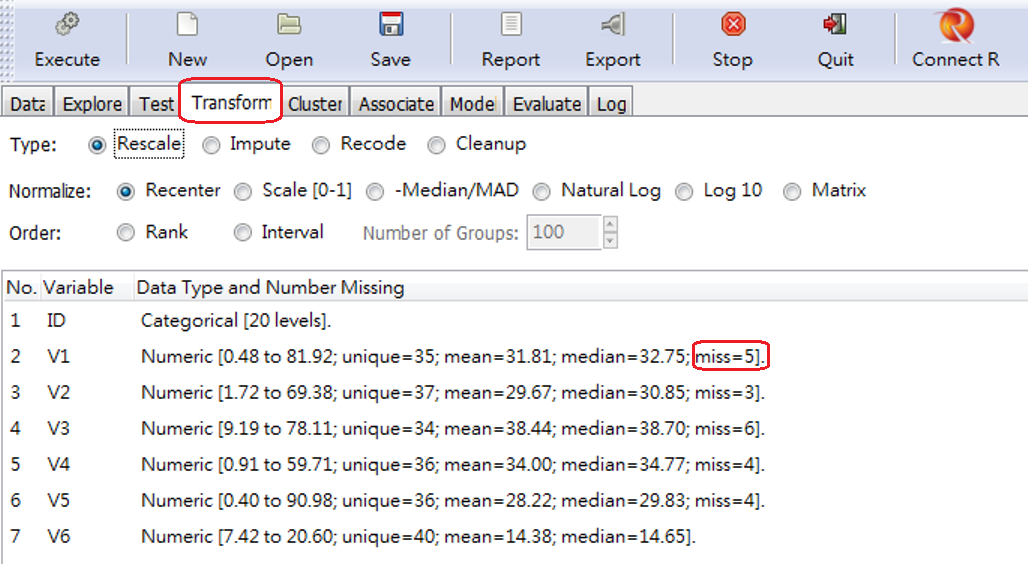
圖 3.4: Rescale(尺度比例重新調整)的選項
資料轉換的使用方法,可以由以下練習,透過實做來解說。
〔練習〕我們將V6做「自然對數轉換」:
首先,選按鈕Natural Log;
其次,用滑鼠點選下方陳列之變數V6。
按Execute後,就會產生新變數RLG_V6,如圖 3.5 。
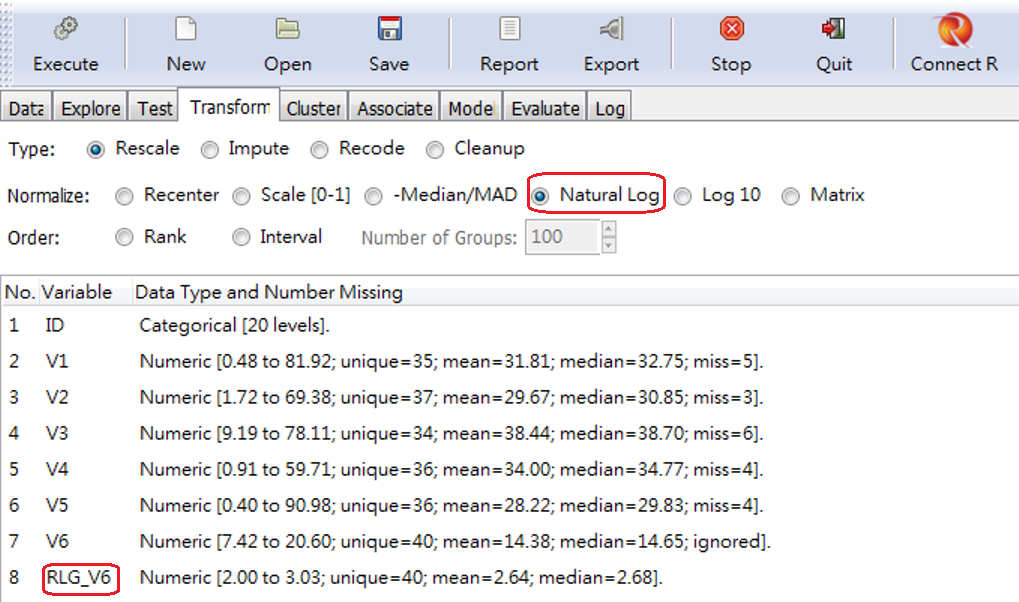
圖 3.5: 對V6做自然對數轉換
回到Data選單,可以看到產生之新變數。如果要對變數做進一步的管理,例如刪除,可以用View 或Edit打開資料,然後框住你要刪除的變數,點一下滑鼠右鍵,就可以出現很多功能,如圖 3.6 。但是,只有Edit處才有真正對資料編輯的功能,View處的編輯僅是暫時性的,因為當我們將視窗關閉再重新開啟時,方才被刪除的資料又會再重新出現。
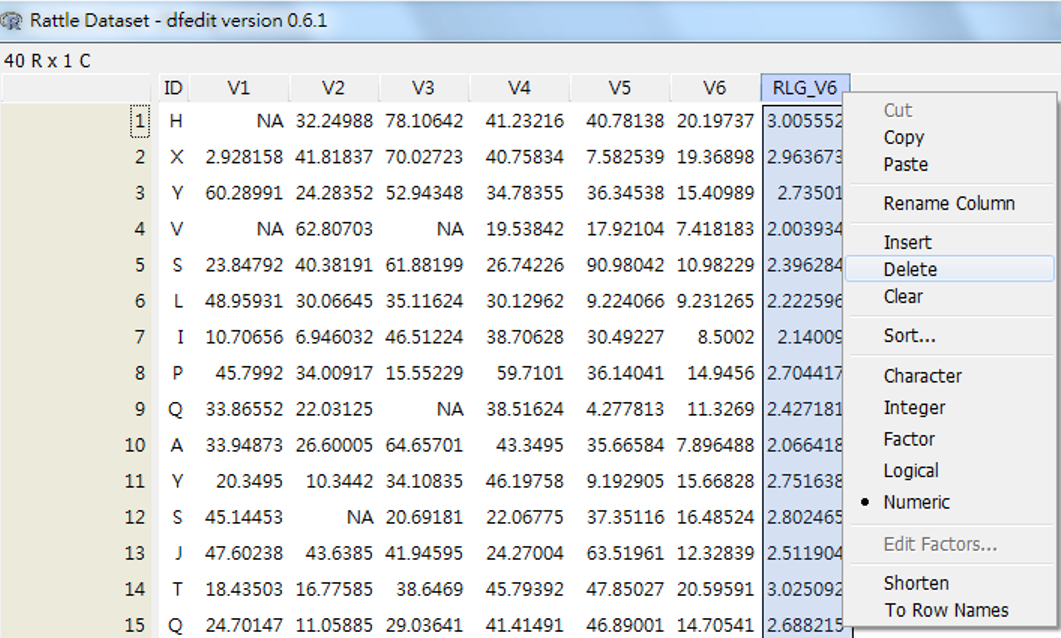
圖 3.6: 資料檢視
選擇插補(Impute)處理缺值後,就會有如何插補的按鈕選項。Zero 就是補0;Mean是用該變數的平均數填入,如圖 3.7 所示,其餘同理。
圖 3.7: Impute (插補) 的選項
〔練習〕請將V4的缺值,以中位數(Median)和眾數(Mode)插補。
Recode 則是將變數「更換類型」或是「產生分類」,以圖 3.8 為例,我們選V6執行4分量(Quantiles)的分類,就會產生一筆新數據,將每個對應值所屬分量標示出來,產生一筆新變數BQ4_V6,如圖 3.8 。
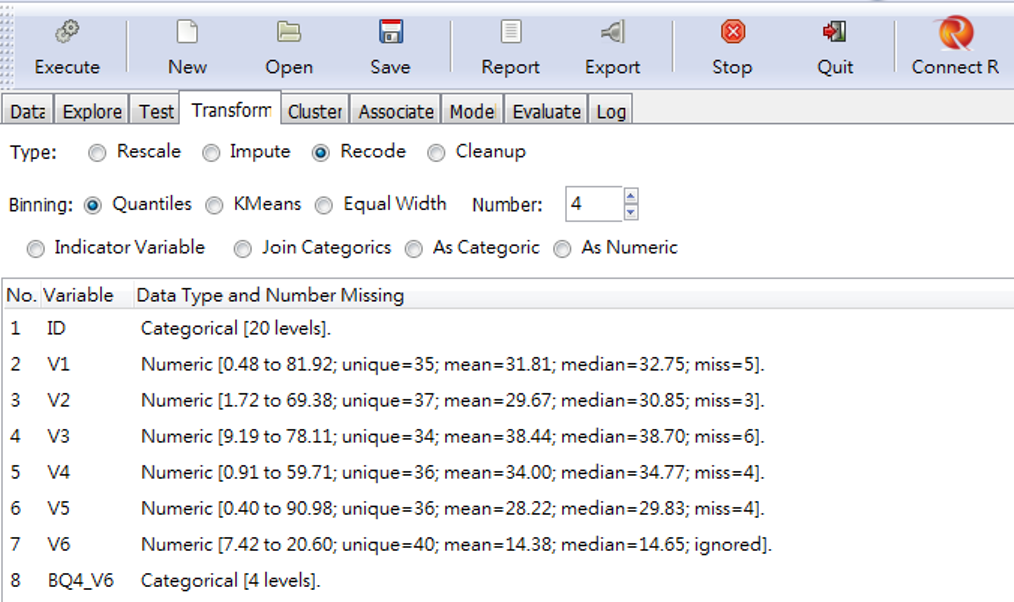
圖 3.8: Recode(重新編碼)的選項
切換回Data,由Edit 處打開看一看方才產製的數據,如後續不須要用的話,就在此把它刪除Delete,如圖 3.9。
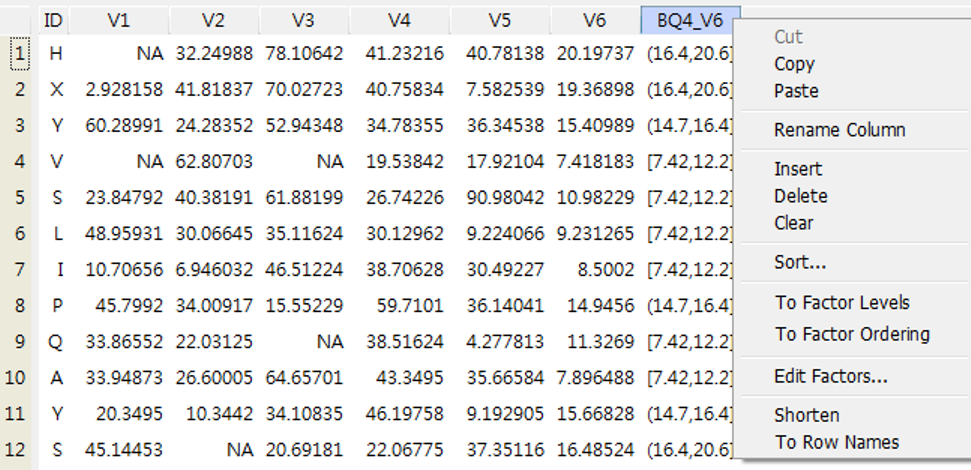
圖 3.9: 滑鼠右鍵顯現功能選單
〔練習〕我們載入的數據,有一筆ID是字串,在Recode處,請選Indicator Variable,看一看這個功能是在做什麼?
另外,As Categoric 是很常用的項目,尤其在glm迴歸時,目標變數如果不是顯示出類別,只有 (0, 1) 數字,模型估計結果的顯示會不夠清楚。我們載入資料MovieDataSet_4Gary.csv,如圖 3.10 。這筆資料是探勘電影票房等級(Class),和哪一些因素有比較強的關聯,目標變數是Class:票房等級,分9級。這個目標變數。由最右邊9個欄位綜合成。如下,其餘類推
=1,倒數第9個LT_1M代表less-than 1 million(少於1百萬美金);
=9,最後一欄GT_200M代表greater-than 200 million(高於2億美金)。
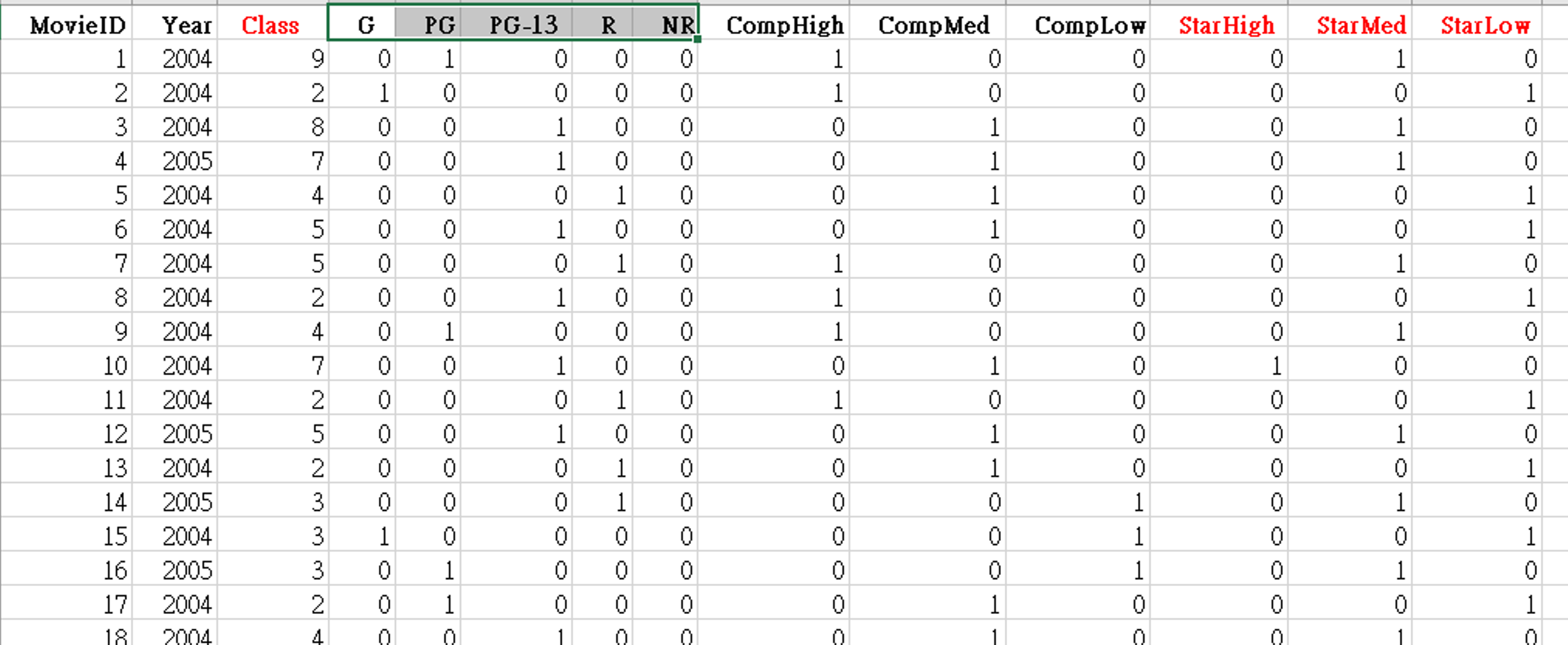
圖 3.10: MovieDataSet_4Gary.csv
我們將Class轉換為As Categoric,之後會產生一筆新變數 TFC_Class。我們必須在Data頁面將之調整為Target,且Execute才能使用。兩個結果的估計如圖 3.11 和圖 3.12 ,差別在於輸出時,轉換後變數比較清楚知道原級距9個,是如何顯示。
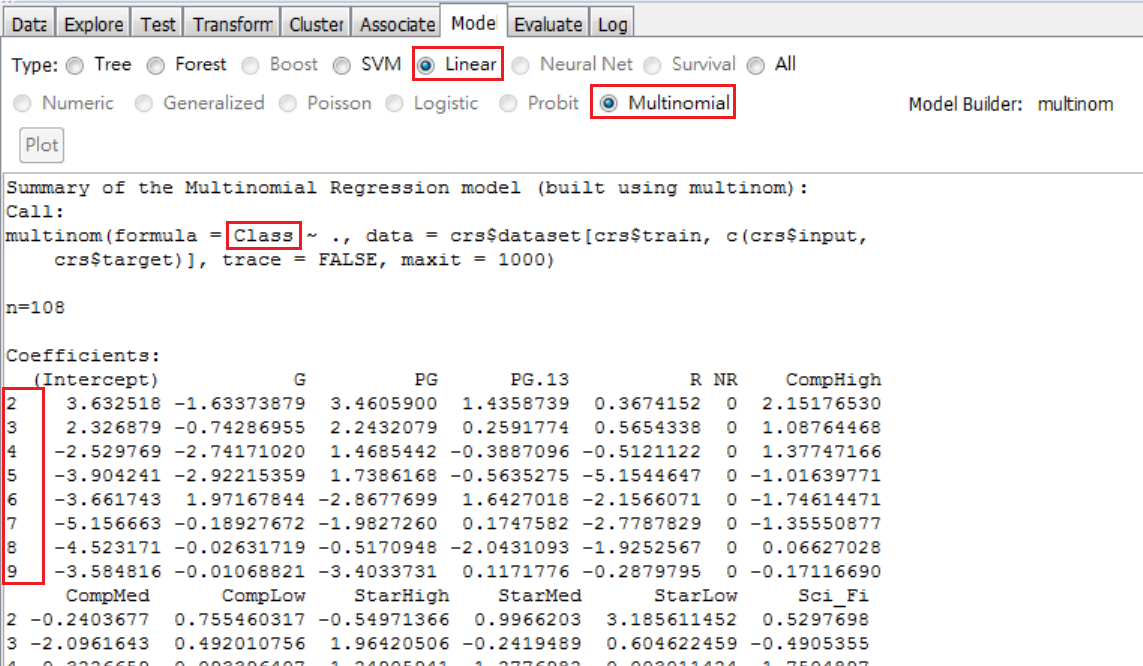
圖 3.11: 以數值Class為目標變數(依賴變數)
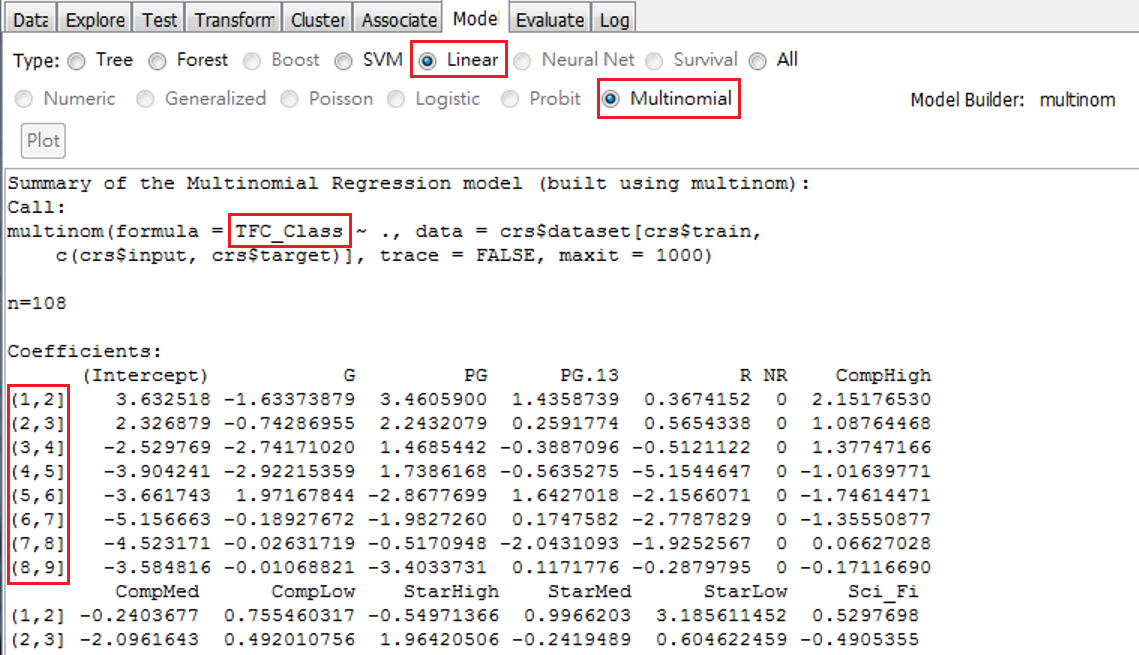
圖 3.12: 以類別TFC_Class為目標變數(依賴變數)
Recode其餘變數轉換功能,只要實際練習,就會瞭解。
最後,圖 3.13 的 Cleanup顧名思義就是清理資料中的變數或變數內的缺值或Data頁面的選項。
很簡單,請直接試一試就一清二楚。
圖 3.13: Cleanup(清理資料)的選項
Delete Ignored: 刪除Data 頁面被歸為Ignored的變數
Delete Selected: 刪除下方選擇變數
Delete Missing: 刪除缺值。此處需注意,刪除具有缺值的「變數」,如圖 3.14 。
圖 3.14 中執行選項後,會出現對話視窗詢問刪除的內容,如圖有5個變數要刪除。這種刪除法,會將整個變數移除,變數只要有一個缺值,就移除,而且移除的方式是將整的變數由記憶環境中移除,但是不會覆寫原來的資料檔。如果發現這樣移除是錯的,只要再載入一次資料就可以。如果這樣的移除是正確的,也要在Data頁面執行Execute一次更新記憶。
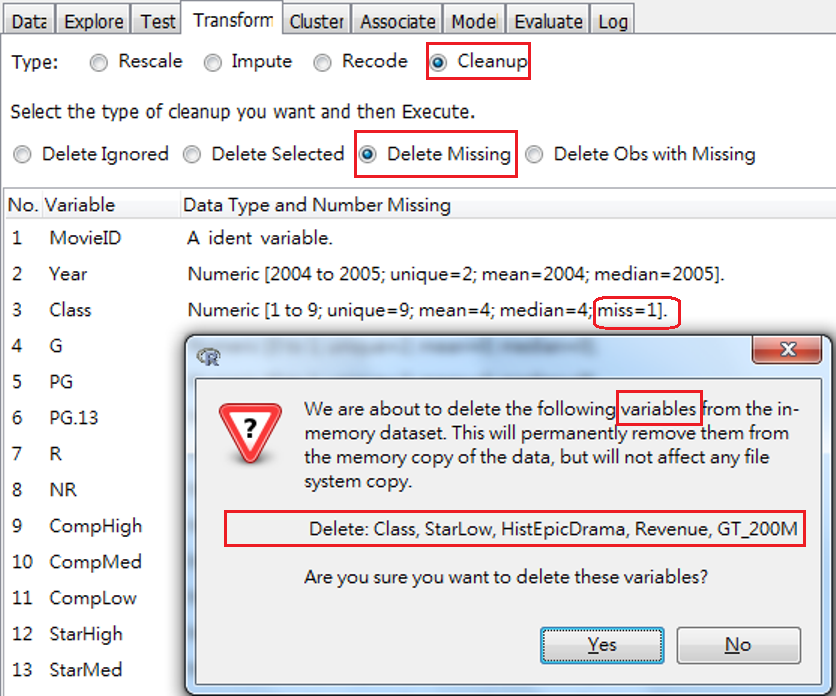
圖 3.14: 刪除具有缺值的變數
Delete Obs with Missing:
刪除缺值。此處需注意,刪除的會是具有缺值的一整列觀察值,如圖 3.15 出現的對話視窗會告知一共刪除多少觀察值,詢問是否要刪除。要注意,是刪除「一整列」。這樣的做法,是因為演算上須要整筆資料都是完整的,一般是計算相關係數矩陣時,會須要這樣做。但是,如果刪除之後會使整個樣本變少,就要考慮了。
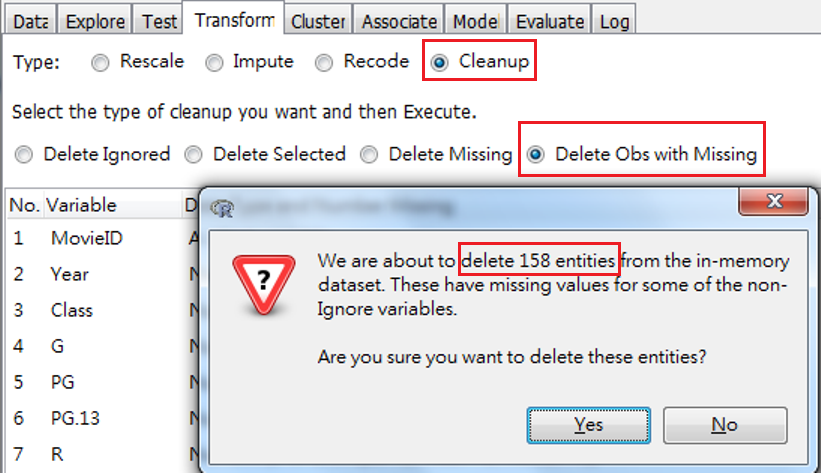
圖 3.15: 刪除具有缺值的一整列觀察值
Transform內的4個資料轉換功能,是R裡面時常會用到的。除了配合在rattle內使用,還可以用來整理資料。整理完,只要按Export,就會另存新檔,如圖 3.16 。rattle自動產生新的檔名,在原檔名後面,增加 _sample。右下角的Save按鈕按下後就會自動儲存。
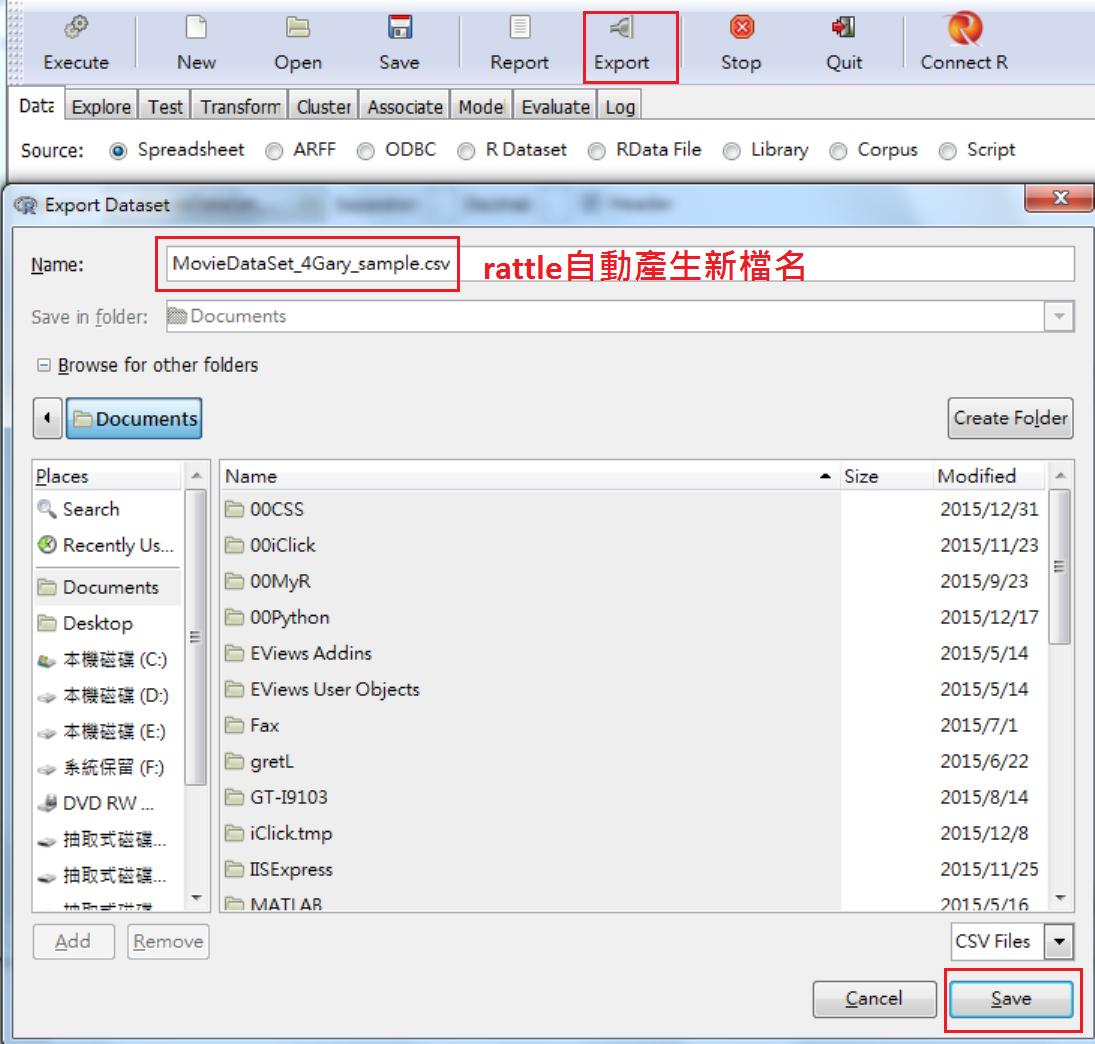
圖 3.16: Export新資料