neighbor - 演算法筆記

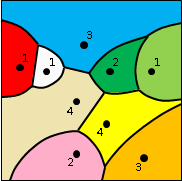
Voronoi diagram

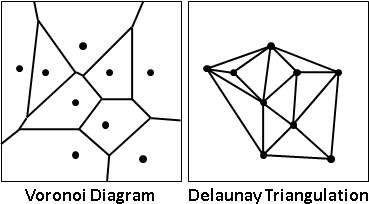
平面上散布許多點。平面上每一處，各自歸類於最近的點；自然而然的，形成了分界線，是中垂線。 Voronoi diagram 是分界線組成的集合。 Voronoi 是發明者的姓氏。

簡單來說，鄰近的點的中垂線，形成 Voronoi diagram 。

Voronoi diagram 隱含著鄰近的資訊，所以「最靠近」、「距離最短」之類的問題，多半可以透過 Voronoi diagram 解決。

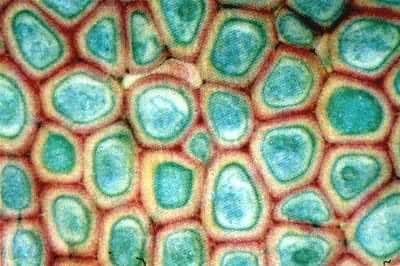
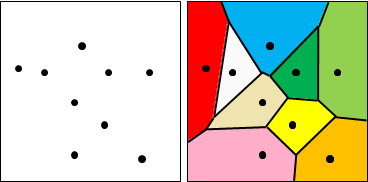
Voronoi diagram 是大自然的圖案，諸如長頸鹿的斑紋、蜻蜓的翅膀、葉片的細胞壁。應用相當廣泛。

UVa 12109

perpendicular bisector

「中垂線」，中學數學，不再贅述。

Line pb(Point a, Point b)
{
// ab中點。
Point c = (a + b) / 2.0;
// ab向量，顛倒、變號，得到法向量。
Point s = b - a;
swap(s.x, s.y);
s.x *= -1;
// 中垂線。兩點得一線。
return (Line){c, c + s};
}

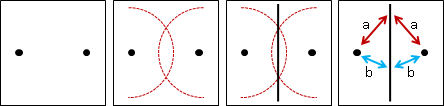
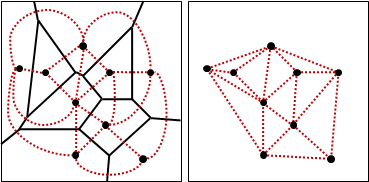
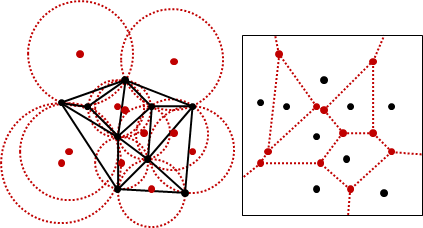
三角形的三中垂線，交於一點，是外接圓圓心，稱作外心。中垂線有等距、平分的感覺，圓有等距、歸心的感覺，兩者關係匪淺。

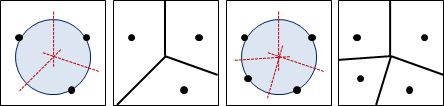
由此可知， Voronoi diagram 一個點至少連著三條邊。

Voronoi diagram 點和邊的數量

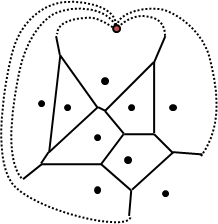
延伸至無限遠的邊，通通接往一個點， Voronoi diagram 就變成平面圖。

運用平面圖歐拉公式 v-e+f=2 ，輔以「一個點至少連著三條邊」的限制，可以推理出 Voronoi diagram 最多有 2N-5 個點、 3N-6 條邊，都是 O(N) 。

演算法（ half-plane intersection ）

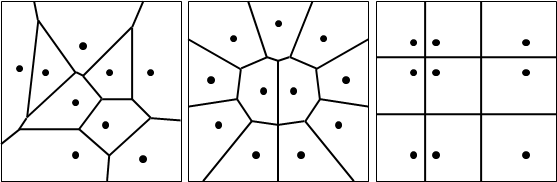
枚舉每一點，求得該點的區域：與其他點形成的 N-1 條中垂線，求半平面交集。時間複雜度 O(N ⋅ NlogN) = O(N²logN) 。

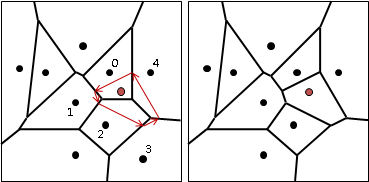
演算法（ incremental method ）

online 演算法，一次加一點。找到當前輸入點相距最近的點，然後以中垂線繞行一圈求得當前輸入點的區域。時間複雜度 O(N²) 。

演算法（ divide-and-conquer method ）

所有點分成左右兩側，分別求出 Voronoi diagram ，然後合而為一。

從左右 convex hull 的外公切線的中垂線開始行進，一旦撞到左右 Voronoi diagram ，就改變行進方向。途中清除多餘的 Voronoi diagram 。

時間複雜度 O(NlogN) 。然而步驟繁雜，運行極慢，不實用。讀者只需知道 Voronoi diagram 存在這麼一個解題策略就行了，不需浪費時間鑽研細節。

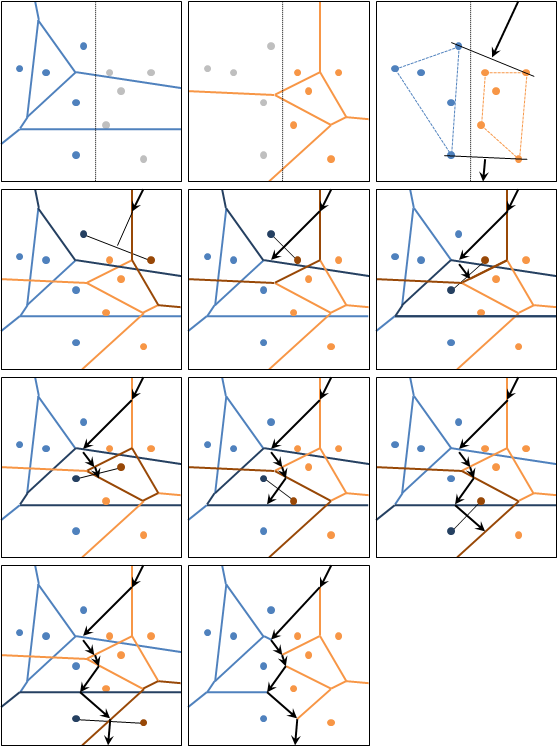
演算法（ Fortune's algorithm ）

平移的掃描線。時間複雜度 O(NlogN) 。

實務上最快的演算法。

Delaunay triangulation

Delaunay triangulation 源自 Voronoi diagram 。

Voronoi diagram 變 Delaunay triangulation ：以直線連結相鄰的點。簡單來說就是平面對偶、邊拉直。時間複雜度 O(N) 。

Delaunay triangulation 變 Voronoi diagram ：以直線連結相鄰的三角形的外接圓圓心，並且補上凸包每一條邊的中垂線。時間複雜度 O(N) 。

Delaunay triangulation 的數量

只有三點以下共圓， Voronoi diagram 與 Delaunay triangulation 只有唯一一種，互相對應。

出現四點以上共圓， Voronoi diagram 仍然只有唯一一種， Delaunay triangulation 則有許多種。

性質： empty circumcircle property

三角形外接圓，內部不含任何點。證明省略。

性質： maxmin angle triangulation

最小角盡量大。證明省略。

Voronoi diagram 是中垂線與距離， Delaunay triangulation 是圓與角度。

演算法（ Lawson's flip algorithm ）

隨意求出一個三角剖分。不斷翻轉不符空圓性質的邊，使最小角逐漸增大（或者最小角不變、次小角增大，以此類推）。每一條邊頂多翻轉一次。時間複雜度 O(N²) 。

演算法（ Bowyer–Watson algorithm ）

online 演算法，一次加一點。不符空圓性質的三角形，形成一個多邊形，清除內部所有邊，重新連接當前點與多邊形頂點，就得到 Delaunay triangulation 。時間複雜度 O(N²) 。

演算法（ divide-and-conquer method ）

所有點分成左右兩側，分別求出 Delaunay triangulation ，然後合而為一。

時間複雜度 O(NlogN) 。然而步驟繁雜，運行極慢，不實用。讀者只需知道 Delaunay triangulation 存在這麼一個解題策略就行了，不需浪費時間鑽研細節。

演算法（ sweep circle algorithm ）

旋轉的掃描線。時間複雜度 O(NlogN) 。

實務上最快的演算法。

Voronoi diagram 各式變種

延伸閱讀：拋物面

點座標 (x, y) 改成 (x, y, x²+y²) ，呈現拋物面。

割面與拋物面的交集，投影至 XY 平面，恰是圓。

點座標 (x, y) 改成 (x, y, x²+y²) ，求得三維凸包。

下凸包，投影至 XY 平面（自下方無限遠處仰視），恰是 nearest point Voronoi diagram 的對偶圖，也就是 Delaunay triangulation 。

上凸包，投影至 XY 平面（自上方無限遠處俯視），恰是 farthest point Voronoi diagram 的對偶圖。

點座標 (x, y) 改成 (x, y, x²+y²) ，呈現拋物面。

兩切點、兩切面的交集，投影至 XY 平面，恰是中垂線。

點座標 (x, y) 改成 (x, y, x²+y²) ，求得切面們的三維包絡面。

下包絡面，投影至 XY 平面，恰是 Delaunay triangulation 。

上包絡面，投影至 XY 平面，恰是 Voronoi diagram 。

nearest neighbor graph

  nearest neighbor graph            各點連往最近鄰居
⊆ Euclidean minimum spanning tree   最近點對相連，形成環則捨棄
⊆ relative neighborhood graph       兩點相連，當其他點距離都更遠
⊆ Gabriel graph                     兩點相連，當外接圓不含其他點
⊆ Delaunay graph (1-skeleton)       三點相連，當外接圓不含其他點

α-shape    https://en.wikipedia.org/wiki/Alpha_shape
β-skeleton https://en.wikipedia.org/wiki/Beta_skeleton
Θ-graph    https://en.wikipedia.org/wiki/Theta_graph
Yao graph  https://en.wikipedia.org/wiki/Yao_graph

ICPC 3270

Euclidean graph

邊的權重，等於二維平面的直線距離。

儘管 Euclidean graph 是二維平面上的圖，但是它跟 planar graph 沒有任何關係。

nearest neighbor search

L₂-norm nearest neighbor search

已知一群點（固定），給定一個點（變動），從中找到最近點。

同義詞： L₂-norm = Euclidean 。 nearest = closest 。 search = query 。

locality-sensitive hashing 。 O(N) 。

L₂-norm all nearest neighbors

已知一群點，求每個點的最近點。顯然涵蓋了「最近點對」。

L₂-norm farthest neighbor search

已知一群點（固定），給定一個點（變動），從中找到最遠點。

我沒有研究。

L₂-norm all farthest neighbors

已知一群點，求每個點的最遠點。顯然涵蓋了「最遠點對」。

窮舉法。 O(N²) 。

farthest Voronoi diagram 。 O(NlogN) 。

動態問題，更新、查詢的平均時間複雜度是 O(log²N) 。

L₂-norm all farthest neighbors on convex hull

無法使用旋轉卡尺。例如一個橢圓。

randomized incremental method 。 O(NlogN) 。

Monge matrix + SMAWK algorithm 。 O(N) 。

UVa 12311

L₂-norm mininum spanning tree

Kruskal's algorithm 。 O(ElogV) = O(N²logN) 。

Prim's algorithm 。 O(N²) 。

Voronoi diagram 。 O(NlogN) 。

L₁-norm all nearest pairs

ICPC 5848

L₁-norm farthest pair

距離公式 |x1 - x2| + |y1 - y2| + |z1 - z2| 。去掉絕對值，共 8 種情況。以 (x1 - x2) - (y1 - y2) + (z1 - z2) 為例，重新整理得到 (x1 - y1 + z1) - (x2 - y2 + z2) 。若前項盡量大、後項盡量小，則距離越大。

窮舉 8 種正負號配置情況（因為對稱，其實只需 4 種）。對於一種情況，窮舉每個點，記錄最大值、最小值。最大值減最小值，即為所求。時間複雜度 O(N) 。

struct Point {int x, y, z;} p[10];
int f(int a, int b, int c)
{
int max = -1e9, min = 1e9;
for (int i=0; i<10; i++)
{
int v = a * p[i].x + b * p[i].y + c * p[i].z;
max = std::max(max, v);
min = std::min(min, v);
}
return max - min;
}
float farthest_pair()
{
return max(max(f(1,1,1), f(1,1,-1)), max(f(1,-1,1), f(-1,1,1)));
}

UVa 11012

L₁-norm mininum spanning tree

邊數降為 4N ，可套用 Kruskal's algorithm 。 O(NlogN) 。