Array

儲存一個數列，直覺的方式是使用一個陣列。

更新第k項：O(1)。

插入第k項、刪除第k項：需要挪移資料。O(N)。

區間總和、區間最大值、區間最小值：逐個累計。O(N)。

List

更新第k項、插入第k項、刪除第k項：需要定位。O(N)。

區間總和、區間最大值、區間最小值：逐個累計。O(N)。

串列與陣列的步驟數量，相比之下，顯然串列小於等於陣列──然而兩者的時間複雜度都是O(N)。可以發現現行的時間複雜度標記方式，不是那麼精準，無法區分兩者的快慢差異。

Unrolled Linked List

更新第k項：O(A)。

插入第k項、刪除第k項：O(A + 2B)到O(2A + B)。

使用sqrt decomposition，三者皆是O(sqrtN)。

區間總和、區間最大值、區間最小值：每塊額外記錄數值，先查詢塊、再查詢元素。O(A)到O(A + 2B)。

使用sqrt decomposition，三者皆是O(sqrtN)。

如果只需更新、查詢，不需插入、刪除，此時可以用陣列代替串列，容易實作。

UVa 12003 11922 11990 12345

粗淺的理解、錯誤的方式

既然BST是儲存大量數字的資料結構，我們嘗試運用BST來儲存一串數列。

數列的索引值是有序的，BST是有序的，我們嘗試以索引值大小順序，作為BST的排序依據。BST的每個節點，額外記錄數列的數值。

雖然可以迅速更新第k項，但是無法迅速插入第k項、刪除第k項，索引值無法保持連續整數。

深刻的理解、正確的方式

Search Tree、Heap的功能是排順序，排序依據不見得得是數字大小順序，排序依據也不見得要儲存於節點之中。比如圖論領域的資料結構「Link–Cut Tree」所使用的BST，排序依據是樹上節點的父子順序。

令左子樹是索引值較小的項、右子樹是索引值較大的項。排序依據，仍是索引值大小順序，但是排序依據不必儲存於節點之中。

更新第k項：就是找到BST第k名。BST的每個節點，額外記錄子樹的節點個數，以便快速得到名次。

插入第k項：先找到BST第k名，如果沒有右小孩，就挪至右小孩；如果擁有右小孩，就挪至次大節點（即BST第k+1名）的左小孩。然後原本第k名的位置，存入數列第k項。最後記得更新擴充資訊，由樹葉往樹根方向。

刪除第k項：先找到BST第k名，如果沒有小孩，就直接刪除；如果擁有左小孩、沒有右小孩，就拿左子樹頂替第k名；如果擁有左小孩、擁有右小孩，就拿次大節點頂替第k名，再拿次大節點的右子樹頂替次大節點（此時次大節點無左小孩）。最後記得更新擴充資訊，由樹葉往樹根方向。

不必死背這些流程。只要細心觀察BST，很容易推理出來。

如果旋轉節點、平衡BST，那麼更新、插入、刪除、尋找次大節點的時間複雜度從O(N)變成O(logN)。

區間總和、區間最大值、區間最小值：每個節點額外記錄該子樹所有節點的總和、最小值、最大值！交給讀者。

任意區間的最大（小）區間和：交給讀者。

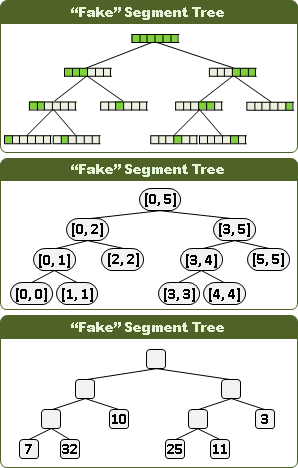
“Fake” Segment Tree【尚無正式名稱】

此資料結構由競賽選手發明，沒有發表為正式的學術論文。目前發現最早出現於Baltic OI 2001: Mars Maps，官方解答提供了此資料結構的程式碼。

此資料結構最初沒有特定名稱。傳入中國之後，競賽選手將名稱定調為Segment Tree，創造大量相關題型，例如SPOJ: GSS3，令Segment Tree之名稱被發揚光大。然而「Segment Tree」是既有的資料結構名稱，所以此資料結構勢必另取他名，以免混淆。

建立資料結構

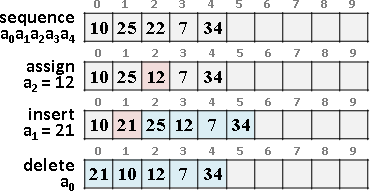
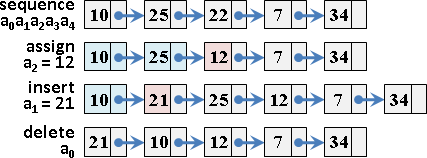
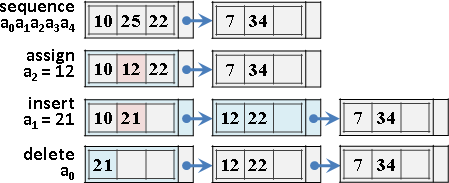
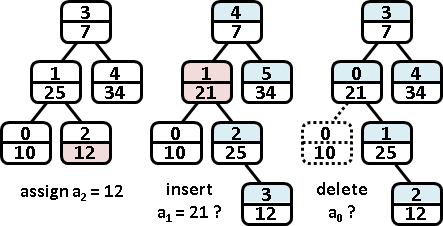
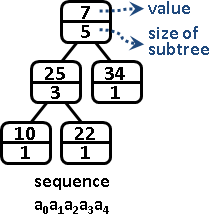
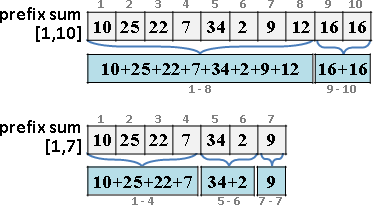
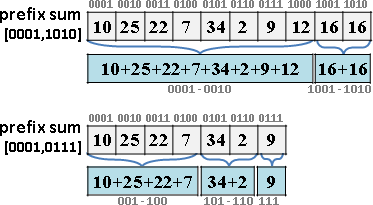
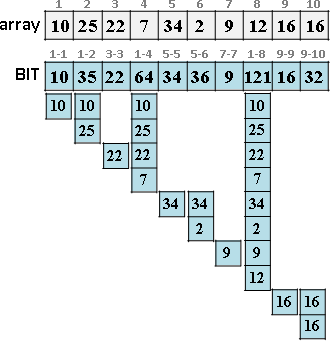
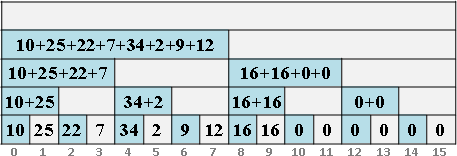
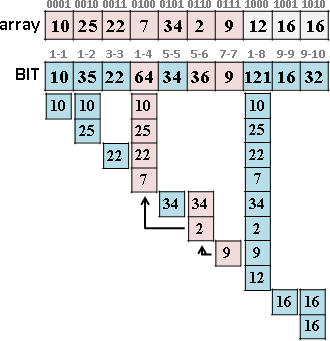
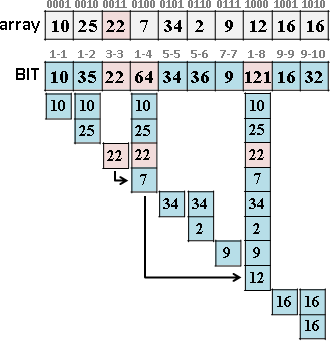
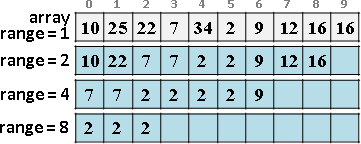
遞迴二分區間，樹葉存放數列，一個樹葉儲存一項；非樹葉存放擴充資訊，諸如區間總和、區間最大值、區間最小值。

二元樹的資料結構，採用陣列，投機取巧省去new和delete。

const int N = 100; int array[N]; // 數列 struct Node { // int L, R; // 其下所有樹葉的數列索引值範圍 int sum; // 其下所有樹葉的區間總和 // int min; // 其下所有樹葉的區間最小值 // int max; // 其下所有樹葉的區間最大值 } node[512]; // 用陣列模擬二元樹 // 用陣列模擬二元樹：左小孩、右小孩 int LC(int i) {return i*2;} int RC(int i) {return i*2+1;} void build(int L, int R, int i) { if (L == R) { // 設定樹葉的數值 node[i].sum = array[L]; return; } int M = (L + R) / 2; build(L , M, LC(i)); // 遞迴建立左子樹 build(M+1, R, RC(i)); // 遞迴建立右子樹 // 回溯時順便計算總和 node[i].sum = node[LC(i)].sum + node[RC(i)].sum; } void demo() { // 建立索引值0到99的偽線段樹 for (int i=0; i<N; ++i) cin >> array[i]; // 樹根的索引值是1 build(0, N-1, 1); }

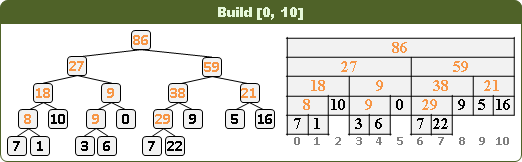
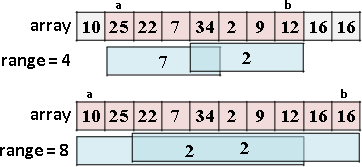
進一步重新配置節點位置，節省記憶體空間。節點[L,R]配置於陣列第L+R格。

原理如同二元搜尋樹，左子樹L+R較小或相等、右子樹L+R較大，導致每個節點的L+R皆相異，例外是樹葉與非樹葉之間的L+R可能相等，此時樹葉配置於原本位置、非樹葉配置於下一格。

節點總共2N-1個，陣列總共2N-1格。空間複雜度O(N)，時間複雜度O(N)。N是數列長度。

const int N = 100; int array[N]; // 數列 int sum[N*2-1]; // 簡便的寫法 int id(int L, int R) { return (L + R) | (L != R); } void build(int L, int R) { if (L == R) { // 設定樹葉的數值 int i = id(L, R); // 陣列索引值 sum[i] = array[L]; return; } int M = (L + R) / 2; build(L , M); // 遞迴建立左子樹 build(M+1, R); // 遞迴建立右子樹 // 回溯時順便計算總和 int i = id(L, R); // 此節點 int l = id(L, M); // 左小孩 int r = id(M+1, R); // 右小孩 sum[i] = sum[l] + sum[r]; } void demo() { // 建立索引值0到99的偽線段樹。 for (int i=0; i<N; ++i) cin >> array[i]; build(0, N-1); }

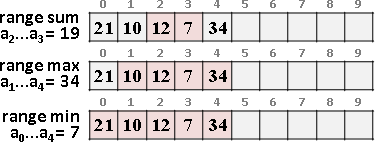
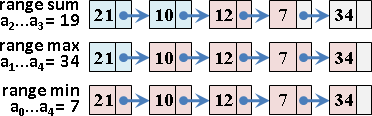
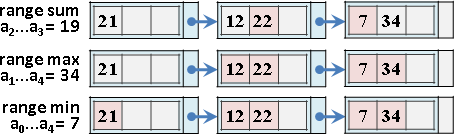
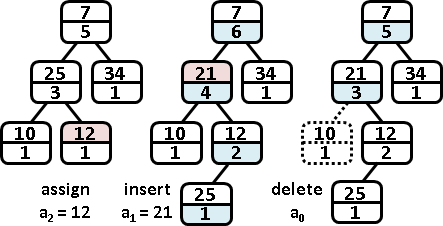
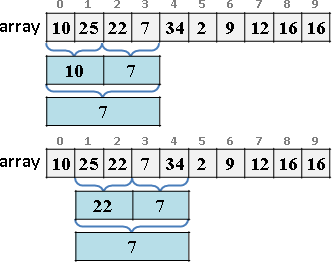
更新第k項、區間總和、區間最大值、區間最小值

類似二元搜尋樹，時間複雜度是樹的深度O(logN)。

int x, n; // 更新位置、數值大小 void update(int L, int R) { if (L == R) { sum[id(L,R)] = n; return; } int M = (L + R) / 2; if (x <= M) update(L , M); // 遞迴更新左子樹 if (x > M) update(M+1, R); // 遞迴更新右子樹 // 回溯時順便更新總和 sum[id(L,R)] = sum[id(L,M)] + sum[id(M+1,R)]; } int x1, x2, n; // 查詢範圍[x1,x2]並且累計總和 void query(int L, int R) { if (x1 <= L && R <= x2) { n += sum[id(L,R)]; return; } int M = (L + R) / 2; if (x1 <= M) query(L , M); // 遞迴查詢左子樹 if (x2 > M) query(M+1, R); // 遞迴查詢右子樹 } void demo() { // 建立索引值0到99的偽線段樹。 for (int i=0; i<N; ++i) cin >> array[i]; build(0, N-1); // 索引值為5的元素，更新為7。 x = 5; n = 7; update(0, N-1); // 查詢區間[3,3]的總和。 x1 = 3; x2 = 3; n = 0; query(0, N-1); cout << n; }

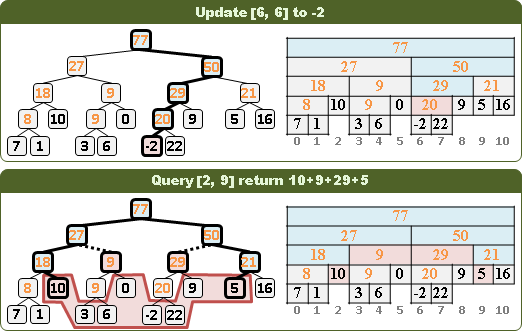
UVa 11297 12299

插入第k項、刪除第k項

不負責任地交給讀者。

推廣到高維度

一維數列推廣到二維陣列、三維陣列。

二維偽線段樹，首先製作一棵第一維度的偽線段樹（X樹），然後每個節點各自接上一棵第二維度的偽線段樹（Y樹）。中文網路稱作「树套树」。

UVa 12698

更新區間：楔子

偽線段樹也可以更新區間。首先簡化問題，把數值改成顏色。如果區間不是相同顏色，就繼續遞迴對半分割下去。如果區間是相同顏色，暫且不分割！

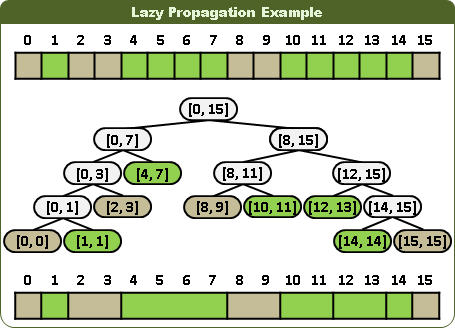
更新第k項，有三大步驟：一、搜尋之時，原有顏色分離，挪往下層。二、就位之時，直接覆蓋顏色，刪除子樹（或者無視子樹）。三、回溯之時，相同顏色合併，挪往上層。

此技巧尚無正式名稱，英文網路稱作「lazy propagation」，中文網路稱作「懒惰标记」，翻譯錯誤。

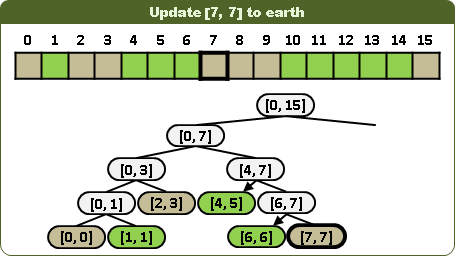
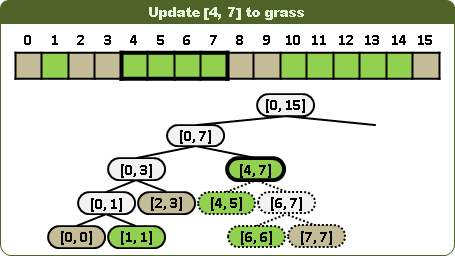
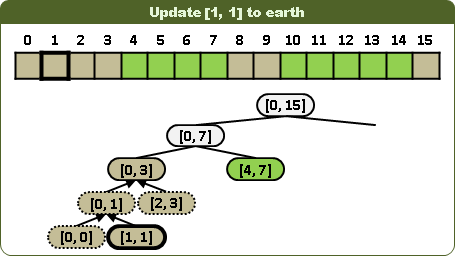
更新區間：視情況左右子樹都得走，並分割更新區間。

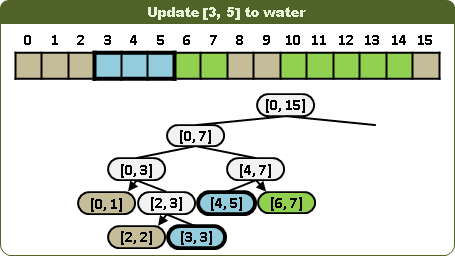
查詢第k項：一旦遭遇顏色，即得答案，不必深入子孫。

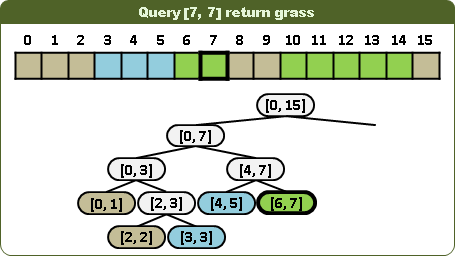
查詢區間顏色是否一致：視情況左右子樹都得走，並分割查詢區間。當節點區間大於等於查詢區間時，一旦遭遇顏色，即可判斷異同，不必深入子孫。當節點區間小於等於查詢區間時，一旦遭遇無色，即得答案為否，不必深入子孫。不能推廣到高維度。

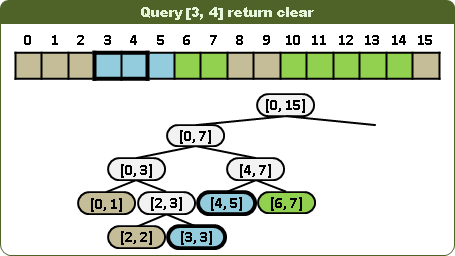
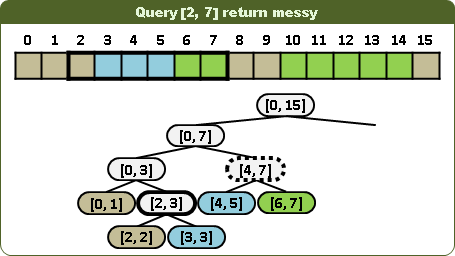
這四項操作的時間複雜度都是O(logN)。

更新區間：統統改為一數值

更新第k項、更新區間：運用「lazy propagation」技巧，凡遭遇已改值的區間，則分離挪往下層。

查詢第k項、查詢區間：凡遭遇已改值的區間，即得答案，不必深入子孫。

查詢區間不能推廣到高維度。

const int N = 100; int array[N]; // 數列 int value[N*2-1]; // lazy propagation void build(int L, int R) { int M = (L + R) / 2; int i = id(L, R); // 此節點 int l = id(L, M); // 左小孩 int r = id(M+1, R); // 右小孩 if (L == R) { value[i] = array[L]; return; } // 內部節點初始化為沒有設值 value[i] = 1e9; build(L , M); build(M+1, R); // 左右相同，合而為一。可不寫。 if (value[l] == value[r]) value[i] = value[l]; } int x1, x2, n; void update(int L, int R) { int M = (L + R) / 2; int i = id(L, R); // 此節點 int l = id(L, M); // 左小孩 int r = id(M+1, R); // 右小孩 if (x1 <= L && R <= x2) { value[i] = n; return; } // 已經設值，恰好相同。可不寫。 if (value[i] == n) return; // 一分為二，撥草找路。 if (value[i] != 1e9) { value[l] = value[r] = value[i]; value[i] = 1e9; } if (x1 <= M) update(L , M); if (x2 > M) update(M+1, R); } //int x, n; int x; void query(int L, int R) { int i = id(L, R); // 此節點 /* // 已被下方程式碼處理掉，不必寫。 if (L == R) { n = value[i]; return; } */ if (value[i] != 1e9) { n = value[i]; return; } int M = (L + R) / 2; if (x <= M) query(L , M); if (x > M) query(M+1, R); } void demo() { // 建立索引值0到99的偽線段樹。 for (int i=0; i<N; ++i) cin >> array[i]; build(0, N-1); // 區間[3,7]所有數值改為5。 x1 = 3; x2 = 7; n = 5; update(0, N-1); // 查詢第5個元素。 x = 5; query(0, N-1); cout << n; }

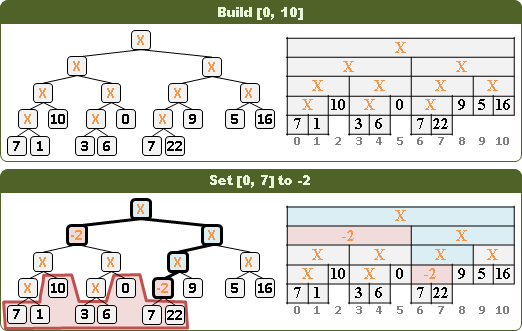
更新區間：統統增減一數值

更新第k項、更新區間：直接在對應區間累計增減值。

查詢第k項：累加路線上的增減值。

似乎無法查詢區間。

這似乎也被歸類於「lazy propagation」技巧。

UVa 11402 11992

楔子

BST和FST要實作很久，趕時間的競賽選手避之唯恐不及。如果不需要插入第k項、刪除第k項，只需要更新第k項、查詢區間，此時就可以採用特殊資料結構，編寫較少程式碼。

只能更新第k項、查詢區間：Bottom-up “Fake” Segment Tree
只能更新第k項、查詢區間總和：Binary Indexed Tree
只能更新第k項、查詢區間極值：Sparse Table

Bottom-up “Fake” Segment Tree【尚無正式名稱】

2010年由競賽選手清华大学张昆玮《统计的力量——线段树全接触》提出。我不清楚是否已有正式學術論文。

讀者須具備「Bitwise Operation」基礎。

int array[(1<<9)-2]; // 數列 int sum[1<<10], T; void build(int N) { int i; for (T=1; T<N+2; T<<=1) ; sum[T] = 0; for (i=0; i<N; ++i) sum[T+1+i] = array[i]; for (++i; i<T; ++i) sum[T+i] = 0; for (i=T-1; i; --i) sum[i] = sum[2*i] + sum[2*i+1]; } // 更新範圍[i,i]、更新為數值n void update(int i, int n) { sum[i += T] = n; for (; i^1; i>>=1) sum[i>>1] = sum[i] + sum[i^1]; } // 查詢範圍[i,j]並且累計總和 int query(int i, int j) { int n = 0; for (i+=T-1, j+=T+1; i^j^1; i>>=1, j>>=1) { if (~i & 1) n += sum[i^1]; if (j & 1) n += sum[j^1]; } return n; }

Binary Indexed Tree（Fenwick Tree）

存放一串數列，可以快速算出任意區間的總和。

可以更新數值，但是不能插入、刪除數值。

閒置陣列第零格。觀察累積和，切割成數段。切割方向：索引值由小到大。切割長度：二的次方，數量級盡量大。

索引值化作二進位，上述行為即是：索引值逐次刪去最低位的1。

10的二進位是1010。
刪去最低位的1，切割成 1010 ~ 1000+1，剩下1000。
刪去最低位的1，切割成 1000 ~ 0000+1，剩下0000，結束。

7的二進位是111。
刪去最低位的1，切割成 111 ~ 110+1，剩下110。
刪去最低位的1，切割成 110 ~ 100+1，剩下100。
刪去最低位的1，切割成 100 ~ 000+1，剩下000，結束。

每種累積和，皆實施切割，總共只有N種區段！N個區段和，依序儲存於陣列，得到Binary Indexed Tree。是陣列、不是樹。

Binary Indexed Tree得視作偽線段樹的精簡版本：擴充資訊是區間總和；移除樹根及全部右小孩。

計算第1項到第k項的總和

挑出對應的區段，進行累加。

更新一項數值

看看哪些區段包含這一項，補上差值。

複雜度

建立時間為O(NlogN)，建立空間為O(N)，更新一項數值的時間是O(logN)，計算任意區間總和的時間是O(logN)。

註：採用偽線段樹的建立手法，建立時間變為O(N)。

const int N = 10000000; int t[N+1]; // 第零格無作用，數列是從第一項到第N項。 // 快速求出最低位的bit。這是其中一種方式。 int lower_bit(int n) { return n & -n; } // value[1] + value[2] + ... + value[n] int sum(int n) { int s = 0; while (n > 0) { s += t[n]; n -= lower_bit(n); } return s; } // value[n] += d void add(int n, int d) { while (n <= N) { t[n] += d; n += lower_bit(n); } } // value[a] + value[a+1] + ... + value[b] int query(int a, int b) { if (a > b) swap(a, b); return sum(b) - sum(a-1); } const int N = 10000000; int t[N]; // 數列是從第零項到第N-1項。 // value[0] + value[1] + ... + value[n] int sum(int n) { int s = 0; while (n >= 0) {s += t[n]; n = (n & (n+1)) - 1;} return s; } // value[n] += d void add(int n, int d) { while (n < N) {t[n] += d; n |= n + 1;} } // value[a] + value[a+1] + ... + value[b] int query(int a, int b) { if (a > b) swap(a, b); return sum(b) - sum(a-1); // 小心a-1可能是-1，會超過陣列邊界。 }

UVa 11423 11610

推廣到高維度

Binary Indexed Tree可以推廣到高維度，建立方法是逐步處理各維度。以二維為例：矩陣切成一條一條的橫條，每個橫條分別建立BIT，每個橫條都有N種區段；然後針對每一種區段，再分別建立垂直方向的BIT。

建立時間為O(XlogX ⋅ YlogY ⋅ ...)，建立空間為O(XY...)，更新一項數值的時間是O(logX ⋅ logY ⋅ ...)，計算任意矩形區域總和的時間是O(2ᴰ ⋅ logX ⋅ logY ⋅ ...)。

const int X = 10000000, Y = 10000000; int t[X][Y]; // value[x][y] += d void add(int x, int y, int d) { // 找出 t[x] 這個橫條 while (x < X) {addy(x, y, d); x |= x + 1;} } void addy(int x, int y, int d) { while (y < Y) {t[x][y] += d; y |= y + 1;} } // sigma value[0...x][0...y] int sum(int x, int y) { int s = 0; while (x >= 0) {s += sumy(x, y); x = (x & (x+1)) - 1;} return s; } int sumy(int x, int y) { int s = 0; while (y >= 0) {s += t[x][y]; y = (y & (y+1)) - 1;} return s; } int sum(int x1, int x2, int y1, int y2) { if (x1 > x2) swap(x1, x2); if (y1 > y2) swap(y1, y2); // 切成四個長方形，然後使用取捨原理。 return sum(x2, y2) - sum(x1-1, y2) - sum(x2, y1-1) + sum(x1-1, y1-1); // 小心x1-1、y1-1可能是-1，會超過陣列邊界。 }

UVa 11601

Sparse Table【註：古代名稱，今日看來詞不達意。】

存放一串數列，可以快速算出任意區間，其中一個最小（大）值的所在位置。有人稱作Range Minimum Query問題。

不能更新、插入、刪除數值。

依序求出寬度為1、2、4、8、……的區間最小值，區間的所有可能位置都要算一遍。兩個窄區間可以快速合成出一個寬區間。

將寬度為1、2、4、8、……的區間最小值，儲存於表格。

t(i, j) =
 { min{ t(i-1, j), t(i-1, j+2^(i-1) }  , if i > 0
 { value[j]                            , if i = 0

實作時，通常表格中記錄的是索引值、指標，而不是直接記錄數值的最小值。

計算區間最小值（的索引值）

查詢時，先從表格中找到寬度略短於（相等於）查詢區間的區間，以靠左、靠右的兩條等寬區間，求得查詢區間的最小值：

複雜度

建立時間為O(NlogN)，建立空間為O(NlogN)，計算任意區間最小值的時間是O(1)。

const int N = 1000000; const int logN = ceil(log(N)); int value[N]; int t[logN][N]; // t[i][j]儲存區間[j, j+2ⁱ-1]的最小值位置 void build() { // 寬度為1的區間最小值位置 for (int i=0; i<N; ++i) t[0][i] = i; // 寬度為2、4、8、……的區間最小值位置 for (int i=1; (1<<i)-1<N; ++i) // i < logN for (int j=0; j+(1<<i)-1<N; ++j) { int& L = t[i-1][j]; int& R = t[i-1][j+(1<<(i-1))]; t[i][j] = (value[L] <= value[R] ? L : R); } } // 找出最小值位置 int query(int a, int b) { int d = abs(b - a) + 1; int p = 31 - __builtin_clz(d); // evil O(1) int& L = t[p][a]; int& R = t[p][b-(1<<p)+1]; return value[L] <= value[R] ? L : R; } const int N = 1000; const int logN = ceil(log2(N)); int value[N]; int t[logN][N]; // t[i][j]儲存區間[j, j+2ⁱ-1]的最小值 void build() { // 寬度為1的區間最小值 for (int i=0; i<N; ++i) t[0][i] = value[i]; // 寬度為2、4、8、……的區間最小值 for (int i=1; (1<<i)<=N; ++i) for (int j=0; j+(1<<i)<=N; ++j) t[i][j] = min(t[i-1][j], t[i-1][j+(1<<(i-1))]); } // 找出最小值 int query(int a, int b) { int p = 31 - __builtin_clz(abs(b - a) + 1); return min(t[p][a], t[p][b-(1<<p)+1]); }

UVa 11235

推廣到高維度

這個資料結構可以推廣到高維度，建立方法是逐次處理各維度即可。以二維為例，先把矩陣切成一條一條的橫條，每個橫條都建立1D Sparse Table；然後以第一條橫條的表格為基礎，表格中的每一個子問題，都建立垂直方向的1D Sparse Table，如此便完成了二維的版本。

建立時間為O(XlogX ⋅ YlogY ⋅ ...)，建立空間為O(XlogX ⋅ YlogY ⋅ ...)，計算任意矩形區域最小值的時間是O(2ᴰ)。

const int X = 1000, Y = 2000; const int logX = ceil(log(X)), logY = ceil(log(Y)); int value[X][Y]; int t[logX][X][logY][Y]; void build() { for (int i=0; i<X; ++i) for (int j=0; j<Y; ++j) t[0][i][0][j] = value[i][j]; // 先計算水平方向 for (int k=0; k<Y; ++k) for (int i=1; (1<<i)<=X; ++i) for (int j=0; j+(1<<i)<=X; ++j) t[0][k][i][j] = min( t[0][k][i-1][j], t[0][k][i-1][j+(1<<(i-1))] ); // 再整合垂直方向 for (int i=0; (1<<i)<=X; ++i) for (int j=0; j<X; ++j) for (int p=1; (1<<p)<=Y; ++p) for (int q=0; q+(1<<p)<=Y; ++q) t[p][q][i][j] = min( t[p-1][q][i][j], t[p-1][q+(1<<(p-1))][i][j] ); } // 找出最小值 int query(int x1, int x2, int y1, int y2) { int x = 31 - __builtin_clz(abs(x2 - x1) + 1); int y = 31 - __builtin_clz(abs(y2 - y1) + 1); // 四個位於角落的矩形，大小都是(1<<x) * (1<<y)。 return min( t[x][x1 ][y][y1 ], t[x][x2-(1<<x)+1][y][y1 ], t[x][x1 ][y][y2-(1<<y)+1], t[x][x2-(1<<x)+1][y][y2-(1<<y)+1] ); }

UVa 11263

Quicksort Tree【尚無正式名稱】

top-down建立。中位數作為pivot，預先排序以求得中位數。

建立O(NlogN)、修改O(logN)、無法插入及刪除、查詢區間內第k名元素O(logN)、查詢區間內元素名次O(log²N)。

Succinct Quicksort Tree（Wavelet Tree）

https://bitbucket.org/MaskRay/rustsnippets/src/e543491ce3ec8c9af95b18cdb8449b7c35b9960b/succinct/uncompressed_wavelet_tree.rs

Merge Sort Tree【尚無正式名稱】

bottom-up建立。

建立O(NlogN)、修改O(logN)、無法插入及刪除、查詢區間內第k名元素O(log²N)、查詢區間內元素名次O(log²N)。

Persistent Merge Sort Tree【尚無正式名稱】

插入及刪除O(logN)。

Cartesian Tree

Cartesian Tree是一種Treap，根的數值小於左右子樹，根的索引值介於左右子樹。

以online方式建立，由左到右讀取陣列元素，每讀取一個元素，就建立一個節點。整棵樹剛好依照DFS順序來回遍歷一次。通常使用stack實作，確保stack的元素依序排好。

僅有理論上的價值，沒有實務上的價值。

All Nearest Smaller Values

±1 Range Minimum Query

尋找區間最小值所在位置，當陣列相鄰數值總是相差±1。

RMQ問題化作LCA問題：利用Cartesian Tree。O(N)。

LCA問題化作±1RMQ問題：利用Euler Tour Technique。DFS到訪次序（作為索引值）、深度（作為元素值）。O(N)。

±1RMQ問題：演算法相當複雜，此處不介紹。建立O(N)、查詢O(1)。

RMQ問題、LCA問題、±1RMQ問題，時間複雜度皆相等，而且到達理論下限。也就是說這三個問題已經被徹底解決了。

僅有理論上的價值，沒有實務上的價值。

Cumulative Sum / Adjacent Difference

累積和（離散積分）：從頭開始、連續數字和。

相鄰差（離散微分）：相鄰數字差。

兩者可以相互抵消！次數一樣多，得到原數列。

數列　 4 -1  6  0  9
累積和 4  3  9  9  18
相鄰差 4 -5  7 -6  9

int array[5] = {4, -1, 6, 0, 9}; int sum[5]; // 累積和 int diff[5]; // 相鄰差 void cumulative_sum() { sum[0] = array[0]; for (int i=1; i<5; i++) sum[i] = sum[i-1] + array[i]; } void adjacent_difference() { diff[0] = array[0]; for (int i=1; i<5; i++) diff[i] = array[i] - array[i-1]; }

區間和

預先以O(N)計算累積和，便能以O(1)計算區間和。

int interval_sum(int i, int j) { if (i > j) swap(i, j); if (i == 0) return sum[j]; return sum[j] - sum[i - 1]; }

二元搜尋樹

集合（索引儲存）、數列（偽線段樹、Binary Indexed Tree）、累積和、二元搜尋，取代二元搜尋樹的各種功能。

集合freq[i]
替freq[i]建立數列資料結構
freq[n]++                <---> 插入數字n     O(logN)
freq[n]--                <---> 刪除數字n     O(logN)
freq[n]累積和            <---> 數字n的名次   O(logN)
freq[n]累積和，二元搜尋k <---> 第k大的數字   O(log²N)

UVa 11525 11990 ICPC 4329

更新區間：統統增減一數值

數列a[i]、數列相鄰差d[i]
替d[i]與i×d[i]建立數列資料結構
d[i]左界+n右界-n <---> a[i]區間+n   O(logN)
d[i]累積和       <---> a[i]第k項    O(logN)
d[i]累積和累積和 <---> a[i]累積和   O(logN)
（用d[i]和i×d[i]算）

Minimum Stack / Minimum Queue