Tree - 演算法筆記

Tree資料結構: Heavy Path Decomposition

Heavy Path Decomposition

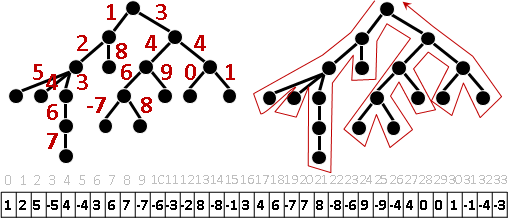
想查詢一棵樹上任意一條路徑的權重，直覺就得到一個O(V)方法，最差情況是這棵樹恰為一條長鏈。

長鏈有很棒的資料結構。只要找出樹上所有長鏈，每條長鏈套用偽線段樹、Binary Indexed Tree、Sparse Table、Binary Search Tree、Binary Heap，就能降低時間複雜度。

找長鏈怎麼找呢？先用一次Graph Traversal算出每棵子樹有多少節點。然後，樹上每個節點各自連向最大的子樹。最後，自然形成了鏈，樹上每個節點都隸屬於某條鏈。

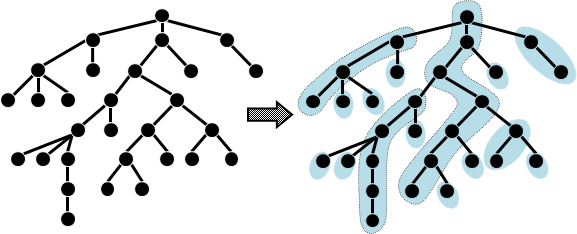
分割一棵樹成為數條鏈，這種手法稱作「重路分解」。中文網路稱作「樹鏈剖分」。

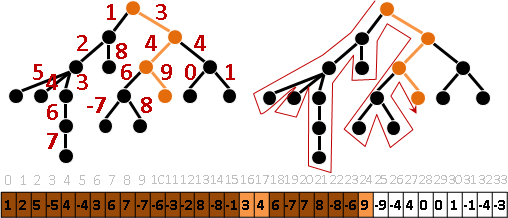
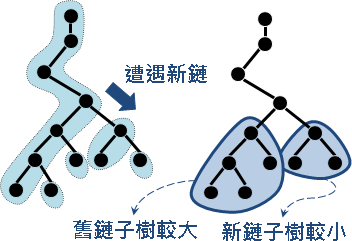
由根往葉走，一旦遭遇新鏈，新鏈子樹小於等於原鏈子樹，剩下的節點數量不到一半，沿途最多遇到logV條鏈。一條路徑藉由LCA拆成兩段，沿途最多遇到2logV條鏈。

時間複雜度

一條鏈最多V個點，一條鏈實施區間查詢為O(logV)。一棵樹最多V條鏈，但是一條路徑最多只遇到2logV條鏈、實施2logV次區間查詢。

樹鏈剖分為O(V)，建立所有長鏈們的資料結構為O(VlogV)，查詢LCA為O(logV)，查詢一條路徑為O(log²V)。

const int V = 100000;
vector<int> adj[V];		// adjacency lists
int parent[V], heavy[V];// 各點的父親、最重小孩
int depth[V], size[V];	// 各點的深度、子樹的點數
int chain[V], head[V];	// 各點所屬的鏈的編號、開頭祖先

void DFS(int i)
{
	size[i] = 1;
	for (int k=0; k<adj[i].size(); ++k)
	{
		int j = adj[i][k];
		if (j == parent[i]) continue;

parent[j] = i;
		depth[j] = depth[i] + 1;

DFS(j);

size[i] += size[j];
		if (heavy[i] == -1 || size[j] > size[heavy[i]])
			heavy[i] = j;
	}
}

// 以DFS實作
void heavy_path_decomposition(int N)
{
	memset(heavy, -1, sizeof(heavy));

parent[0] = -1;
	depth[0] = 0;
	DFS(0);

int c = 0;	// 鏈的編號
	for (int i=0; i<V; ++i)
		if (parent[i] == -1 || heavy[parent[i]] != i)
		{
			// i點是鏈的開頭祖先
			for (int k = i; k != -1; k = heavy[k])
				chain[k] = c, head[k] = i;
			c++;
		}
}

// 或者以BFS實作
int q[V], *qf, *qb;	// BFS queue

void heavy_path_decomposition()
{
	// 計算parent和depth，等同於DFS的divide階段。
	qf = qb = q;
	parent[0] = -1;
	depth[0] = 0;
	*qb++ = 0;
	while (qf < qb)
		for (int i=*qf++, k=0; k<adj[i].size(); ++k)
		{
			int j = adj[i][k];
			if (j == parent[i]) continue;
			parent[j] = i;
			depth[j] = depth[i] + 1;
			*qb++ = j;
		}

// 計算size和heavy，等同於DFS的Combine階段。
	memset(size, 0, sizeof(size));
	memset(heavy, -1, sizeof(heavy));
	for (int k=V-1; k>0; --k)	// 不處理樹根
	{
		int j = q[k], i = parent[q[k]];
		size[j]++;
		size[i] += size[j];
		if (heavy[i] == -1 || size[j] > size[heavy[i]])
			heavy[i] = j;
	}

// 同前
	int c = 0;
	for (int i=0; i<V; ++i)
		if (parent[i] == -1 || heavy[parent[i]] != i)
		{
			for (int k = i; k != -1; k = heavy[k])
				chain[k] = c, head[k] = i;
			c++;
		}
}

int lca(int i, int j)
{
	// 深的上升
	while (chain[i] != chain[j])
		if (depth[head[i]] > depth[head[j]])
			i = parent[head[i]];
		else
			j = parent[head[j]];

return depth[i] < depth[j] ? i : j;
}

int lca(int i, int j)
{
	// i淺j深
	while (chain[i] != chain[j])
	{
		if (depth[head[i]] > depth[head[j]])
			swap(i, j);
		j = parent[head[j]];
	}

if (depth[i] > depth[j])
		swap(i, j);
	return i;
}

ICPC 4960 UVa 12424

Dynamic Trees資料結構: Link–Cut Tree

Link–Cut Tree

http://compgeom.cs.uiuc.edu/~jeffe/teaching/datastructures/2006/notes/07-linkcut.pdf
http://courses.csail.mit.edu/6.851/spring07/scribe/lec04.pdf
http://wenku.baidu.com/view/75906f160b4e767f5acfcedb.html
http://hlworld.diandian.com/post/2012-03-26/17452276
http://www.shuizilong.com/house/archives/tag/动态树/

一、靜態樹：甲、一棵無向樹。
　　　　　　乙、更新一個點(邊)的數值。
　　　　　　丙、查詢一條路徑的最大值、最小值、總和、相異數字數量、......。
二、動態樹：丁、一棵樹，砍斷一條邊，變成兩棵樹。
　　　　　　戊、兩棵樹，增加一條邊，接成一棵樹。

動態樹部分，由於長鏈可能會被切斷，所以「樹鏈剖分」就沒搞頭了。
就只能老老實實的用Link–Cut Tree了。

改變樹根位置的link–cut tree
反轉所有原樹根到新樹根x的邊
先access(x)，此時x會是splay tree的樹根，
然後顛倒整棵splay tree的左右小孩即可
運用反轉標記就簡單多了

改變樹根位置之後
就可以簡單的得到一條路徑ab：先makeroot(a)、然後access(b)即可。

UVa 11994

Tree資料結構: Euler Tour Technique

Euler Tour Technique

想查詢一棵樹上任意一條路徑的權重，直覺就得到一個O(V)方法，最差情況是這棵樹恰為一條長鏈。

長鏈有很棒的資料結構，只要套用偽線段樹、BIT、Sparse Table、BST、Heap，就能降低時間複雜度。

樹一般不是長鏈，那麼要怎麼把樹變成長鏈？樹根為起點，實施DFS，依照遍歷順序，列出每一條邊（點）的權重，得到一條數列，長度為2E：正向經過邊，列出原權重；反向經過邊，列出加了負號的權重。

運用前述的資料結構儲存此數列。樹上一條由淺到深的路徑的權重，即是區間和：參照節點的遍歷順序，較淺節點的首度拜訪時刻，作為區間左邊界；較深節點的首度拜訪時刻減一，作為區間右邊界。從路徑分枝出去的多餘子樹，在區間和之中出現兩次、正負相消，最後剛好剩下路徑的權重。

想要查詢任意一條路徑的權重，就從LCA切斷路徑，得到兩條路徑，都是由淺到深。兩條路徑分頭計算區間和，再相加，即是原路徑的權重。

想要計算LCA，就將權重改成深度，計算區間最小值。

時間複雜度

DFS為O(V)，建立長鏈的資料結構為O(VlogV)，查詢LCA為O(logV)，查詢一條路徑為O(logV)。

Heavy Path Decomposition

遍歷時，優先走向最大的子樹。所有長鏈皆是連續區間。