representation

「重新表示」。換個視角看世界。數據實施變換，改變姿態。

任何一個變換，皆可充作重新表示。例如直角座標變極座標（座標系轉換），例如時域變頻域（傅立葉轉換）。

重新表示有兩種形式。

變換形式：已知原數據，求新數據、求函數。
分解形式：已知新數據，求原數據、求函數。（比較常用）

如果擁有反向變換，那麼兩種形式等價。變換函數移項到等號另一側，得到另一種形式。

向量的重新表示

線性組合：直條的加權平均。（圖例是分解形式）
線性近似：橫條的一一點積。（圖例是變換形式）

不熟悉線性代數的讀者，請見本站文件「basis」，複習一下「矩陣切成直條」、「矩陣切成橫條」兩種觀點。

建立座標軸，向量重新表示為座標值，座標值形成新的向量。

以分解形式為例，向量視作結果，座標軸和座標值視作原因。原因導致結果。我們的目標是找到座標軸和座標值、找到原因。

函數的重新表示

離散向量改成連續函數。就這樣。

順帶一提，函數版本的線性近似，即是「積分轉換integral transform」。座標軸融合成一個二元連續函數，即是「積分核integral kernel」。

工程數學教科書經常出現積分轉換。例如傅立葉轉換就是積分轉換，各種頻率的複弦波就是積分核。

矩陣的重新表示

左乘：數據們實施線性變換。原數據與新數據一一對應。（圖例是變換形式）
右乘：數據們的加權平均數。權重與新數據一一對應。（圖例是變換形式）

例如主成分分析就是左乘（變換形式）。

最佳化

重新表示化作最佳化問題。

min ‖y - Ax‖²          向量的重新表示y = Ax（此例是分解形式）
A,x

min ‖Y - AX‖ꜰ²         矩陣的重新表示Y = AX（此例是分解形式）
A,X

重新表示是困難的問題。同時找到變換函數、變換結果，未知數太多了，最佳化結果總是淪於瞎猜。大家追加各式各樣的限制條件，想方設法讓最佳化結果變得有意義，卻依然淪於瞎猜。

sparse representation

零越多越好。數學式子通常寫成L₀ norm最佳化。

min ‖y - Ax‖ꜰ² + α ‖A‖₀ + β ‖x‖₀     (α ≥ 0 and β ≥ 0)
A,x

向量視作結果，座標軸和座標值視作原因。盡量簡化座標軸、盡量減少使用座標軸，盡量讓原因單純。

當α = 0，演算法是分塊座標下降法。我沒有學會。

《Online Dictionary Learning for Sparse Coding》

sparse matrix factorization

一個矩陣分解成兩個非負矩陣相乘。

min ‖M - AB‖ꜰ² + α ‖A‖₀ + β ‖B‖₀     (α ≥ 0 and β ≥ 0)
A,B

演算法請見本站文件「matrix factorization」。

factorization machine

擬合方程式的交叉項，重新表示為矩陣分解。

交叉項（點積）是相關程度。收集兩兩相關程度，形成矩陣。分解矩陣，推敲原始事物。

sparse principal component analysis

PCA的數學式子有兩種等價寫法，這裡採用第二種。

一、令交叉投影的長度平方總和盡量大。追加限制條件：主成分必須正規正交。

max ‖YᵀX‖ꜰ²   subject to YᵀY = I
 Y

二、令新舊數據的距離平方總和盡量小。追加限制條件：主成分必須正規正交。

min ‖X - YYᵀX‖ꜰ²   subject to YᵀY = I
 Y

限制條件併入目標函數。【尚待確認】

min ‖X - YYᵀX‖ꜰ² + α (‖Y‖ꜰ² - n)     (α ≥ 0)
 Y
min ‖X - YYᵀX‖ꜰ² + α ‖Y‖ꜰ²           (α ≥ 0)
 Y

正確答案的左邊乘上任意的正規正交矩陣，仍是正確答案。為了得到唯一解，再追加限制條件：主成分盡量稀疏。

min ‖X - YYᵀX‖ꜰ² + α ‖Y‖ꜰ² + β ‖Y‖₀   (α, β ≥ 0)
 Y

convex relaxation：L₀ norm改成L₁ norm，方便最佳化。

min ‖X - YYᵀX‖ꜰ² + α ‖Y‖ꜰ² + β ‖Y‖⁎   (α, β ≥ 0)
 Y

Y是正規正交矩陣，幾何意義是旋轉暨鏡射。Y越接近I，L₁ norm就越小。也就是說，旋轉角度盡量小、盡量不旋轉數據。

separable representation

separable matrix：每個直條j，皆存在橫條i，該橫條僅(i,j)處不為零。

separable NMF：好像有多項式時間演算法。

《Algorithmic Aspects of Machine Learning》

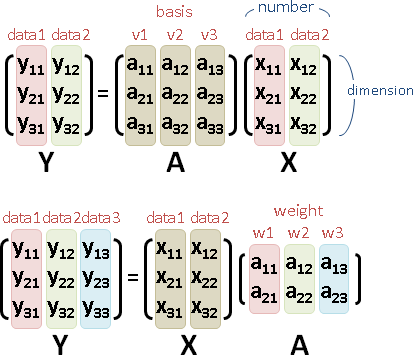
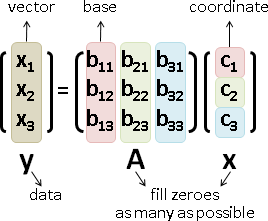
kernel method

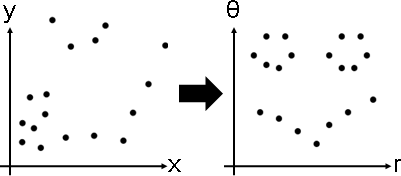
數據實施變換，讓數據變漂亮，方便分群、分類、擬合、對齊、嵌入、……。

但是如何挑選函數呢？一一試驗、碰碰運氣，別無他法。

x̕ = φ(x)
transformation: φ(x)

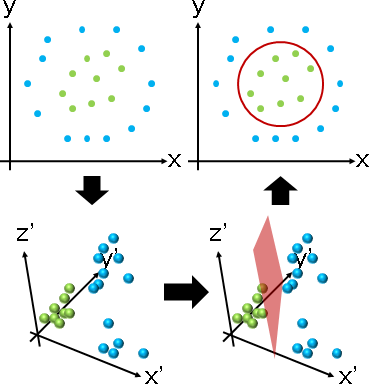
classifier center = (24,22) radius = 10, #(data) = 13 + 7 = 21 p = {{17,8},{21,8},{27,8},{33,10},{37,15},{39,22},{36,30},{30,35},{21,35},{12,32},{12,28},{7,22},{10,14},{18,15},{24,16},{28,18},{16,19},{18,24},{24,23},{31,25},{27,29}}; f[x_] := (x-24)*(x-24); g[y_] := (y-22)*(y-22); h[x_,y_] := Sqrt[2]*(x-24)*(y-22); q = Transpose[{ f[ p[[All,1]] ], g[ p[[All,2]] ], Apply[h, p, {1}] }]; ListPointPlot3D[{q[[1;;13]], q[[14;;21]]}, BoxRatios -> {1,1,1}, PlotStyle -> PointSize[Large]] c = Classify[q -> {"A","A","A","A","A","A","A","A","A","A","A","A","A","B","B","B","B","B","B","B","B"}, "Decision", Method->"SupportVectorMachine"];

一筆數據的誤差，習慣採用距離平方。計算誤差時，數據套用變換函數、距離平方函數，兩個步驟，有點煩。

投機取巧的方式：變換函數、距離平方函數，合併成「數據變換之後的距離平方函數」，簡稱「核函數kernel」。

kernel: k(x,y) = ‖φ(x) - φ(y)‖²

距離平方，恰好由點積組成。於是也有人採用「數據變換之後的點積函數」，簡稱「核函數kernel」。

‖φ(x) - φ(y)‖² = (φ(x) ∙ φ(x)) + (φ(y) ∙ φ(y)) - 2 (φ(x) ∙ φ(y))
kernel: k(x,y) = φ(x) ∙ φ(y)

經典的核函數是radial basis function kernel、heat kernel。

優點：精簡計算步驟，降低時間複雜度。尤其是低維度變高維度的情況下，核函數可以繞過高維度，直接得到距離平方或者點積。

缺點：從核函數無法得知變換函數。不過不知道也沒關係，分群、分類、擬合、對齊、嵌入、……的結果看起來漂亮就好了。

RBF kernel:  k(x,y) = exp(-‖x-y‖² / σ²)                σ is variance
heat kernel: k(x,y) = exp(-‖x-y‖² / 4t) / (4πt)ⁿ⸍²     t is time

先前所有主題，通通可以來個kernel。諸如kernel k-means、kernel SVM、kernel PCA、kernel NMF。學術界有陣子非常流行這種灌水文章，最後弄假成真，kernel變成了教科書的標準配備。

方程組的根、積分變換的座標軸、數據變換之後的距離平方函數，通通叫做kernel。它們之間毫無關聯。

kernel principal component analysis

PCA：

maximize vᵀXXᵀv   subject to vᵀv = 1
maximize vᵀXXᵀv - λ(vᵀv - 1)           Lagrange multiplier
solve XXᵀv = λv                        derivative = 0

數據預先實施變換的PCA：

maximize vᵀΦ(X)Φ(X)ᵀv   st vᵀv = 1     transformation: Φ(X)
maximize vᵀΦ(X)Φ(X)ᵀv - λ(vᵀv - 1)     Lagrange multiplier
solve Φ(X)Φ(X)ᵀv = λv                  derivative = 0
solve Φ(X)Φ(X)ᵀΦ(X)w = λΦ(X)w          kernel trick: v = Φ(X)w
solve Φ(X)ᵀΦ(X)w = λw                  drop Φ(X)
solve K(X)w = λw                       kernel: K(X) = Φ(X)ᵀΦ(X)

數據實施變換之後，數據減去平均數的PCA：

maximize vᵀΦ̄(X)Φ̄(X)ᵀv   st vᵀv = 1     centering: Φ̄(X) = Φ(X)C
maximize vᵀΦ̄(X)Φ̄(X)ᵀv - λ(vᵀv - 1)     Lagrange multiplier
solve Φ̄(X)Φ̄(X)ᵀv = λv                  derivative = 0
solve Φ̄(X)Φ̄(X)ᵀΦ̄(X)w = λΦ̄(X)w          kernel trick: v = Φ̄(X)w
solve Φ̄(X)ᵀΦ̄(X)w = λw                  drop Φ̄(X)
solve K̄(X)w = λw                       kernel: K̄(X) = Φ̄(X)ᵀΦ̄(X)

K̄(X)等於K(X)的橫條直條中心化。

{ Φ̄(X) = Φ(X)C
{ K(X) = Φ(X)ᵀΦ(X)
K̄(X) = Φ̄(X)ᵀΦ̄(X) = CᵀΦ(X)ᵀΦ(X)C = CᵀK(X)C

設計核函數K，精簡計算步驟。

變換函數、核函數不是線性函數，不能寫成矩陣乘法ΦX與KX，只能寫成函數求值Φ(X)與K(X)。Φ(X)與K(X)都是矩陣。

求得K̄(X)最大的特徵值暨特徵向量。w不必還原成v，意思到了就好，精簡計算步驟。

Bayesian inference

引入機率、允許浮動。

用條件機率成立觀點，用貝式定理切換視角。

Gaussian clustering（EM clustering）

每個群集各是一個常態分布。平均數（群集中心）、變異數（群集尺寸與疏密）各自不同。

設定常態分布數量（群集數量）、設定權重（群集尺寸）。常態分布們的加權平均，融合成一個分布──Gaussian mixture model。

實施估計，估計方式採用maximum likelihood，演算法採用EM algorithm。

Bayesian classification（naive Bayes classifier）

迄今都是假定一筆數據只有唯一一種類別。

現在推廣成一筆數據有多種類別，類別是「浮動數字（隨機變數）」，每種類別的機率高低都不同。

p(Cₖ|xᵢ)     unknown, even xᵢ is known

對調主角與配角，切換視角，一種類別也就有多筆數據，數據是浮動數字，每種數據的機率高低都不同。

貝氏定理可以用來切換視角。

p(xᵢ|Cₖ) = p(Cₖ|xᵢ) p(xᵢ) / p(Cₖ)     known, when Cₖ is known

貝氏分類：針對一個類別，讓機率乘積盡量大。

  argmax prod p(Cₖ|xᵢ)
     Cₖ   i
= argmax prod p(Cₖ) p(xᵢ|Cₖ) / p(xᵢ)
     Cₖ   i
= argmax p(Cₖ) prod p(xᵢ|Cₖ)         when p(xᵢ) is uniform distributed
     Cₖ         i

各種類別融合成一個mixture model。

  argmax sum prod p(Cₖ|xᵢ)
     C    k   i
= argmax sum prod p(Cₖ) p(xᵢ|Cₖ) / p(xᵢ)
     C    k   i
= argmax sum prod p(Cₖ) p(xᵢ|Cₖ)     when p(xᵢ) is uniform distributed
     C    k   i
= argmax prod p(xᵢ|C)                mixture distribution
     C    i

Cₖ視作群集。

p(xᵢ|Cₖ)習慣設計成鐘形函數，例如高斯分布。偏離群集中心太遠，超過一定距離，群集關係迅速減弱。功能如同核函數。

p(Cₖ)習慣設定成均勻分布。功能如同權重。

p(xᵢ)習慣假定為均勻分布，各種數據出現數量均等。用來緩和sampling bias。

如果採用Gaussian mixture model，那麼Gaussian clustering與Bayesian classification完全相同。

probabilistic principal component analysis

走火入魔。大家自己看著辦吧。