inclusion–exclusion principle
inclusion–exclusion principle(PIE)
繁中「取捨原理」或「排容原理」、簡中「容斥原理」。
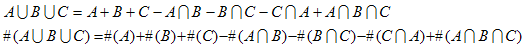
枚舉所有子集合,但是每個子集合有正負號之別──奇數個集合的交集是正號、偶數個集合的交集是負號。
範例:1到100當中不可被3或5或8整除的整數有幾個
3、5、8均兩兩互質。
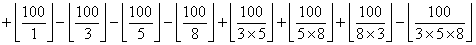
考慮數字之間不互質的情況。
另一種枚舉方式。
UVa 10325 11806 10458
permutation
前言
電腦擅於處理大量資料。處理大量資料,除了大家熟悉的排序和搜尋以外,其實還有排列和組合。
有些問題需要找到最好的排列組合方式。例如求最佳排列的問題travelling salesman problem、assignment problem,例如求最佳組合的問題partition problem、knapsack problem。
想要解決這些問題,最簡單的方法就是枚舉法:枚舉所有可能的排列、組合,一一驗證,從中找到最好的排列、組合。
permutation
數學名詞「permutation」,英文口語「arrangement」。
「排列」。此處的排列是物件,不是函數。
排列就是交換位置。排列也是交換順序。
例如有五筆資料 ●★■▲◆ 這是其中一種排列 ▲●◆★■ 這也是其中一種排列 ●★■▲◆
設定編號,變成數字,方便記載。
12345 例如有五筆資料 ●★■▲◆ 這是其中一種排列 41523 這也是其中一種排列 12345
k-permutation
挑出k個。
例如有五筆資料 12345 取三筆資料的其中一種排列 415 取三筆資料的其中一種排列 523 取三筆資料的其中一種排列 235
編號所有排列
N筆資料的所有排列一共N!種。
一個階乘進位數字,可以代表一個排列。
Lehmer code又稱Cantor expansion:右方數字個數,階乘,作為數量級。右方較小的、尚未出現的數字個數,作為位數。
UVa 941 11525 417 11027 luogu P5367
枚舉所有排列
backtracking:遞迴填入數字。可以得到字典順序。
Steinhaus–Johnson–Trotter algorithm:以Gray code的順序兩兩交換。
Heap's algorithm:判斷奇偶,適時交換。
下一個排列
給定其中一個排列,按照字典順序,找到下一個排列。
把數字想像成數字卡。先拿起一張低位數的數字卡,再利用手上的數字卡,嘗試重新拼出比原本更大一點點的數值(下一個排列)。如果拼不出來,就再多拿起一張數字卡,再拼一遍。
可以直接使用C++標準函式庫的next_permutation()。
UVa 146 845
consecutive ones problem
N個人,排成一直線。限制某些人一定要排在一起,這樣的限制有許多組,必須同時滿足;如果限制過多,也可能無解。問有幾種排法、列出所有排法。
建立一個矩陣。令一個row代表一個限制,要排一起的人標1。兩個column交換,就等於一直線中的兩個人對調位置。不斷交換column,當每個row各自都連成連續的1,就形成一組解了!
為了快速解決這個問題,而發明了PQ tree資料結構,時間複雜度O(NM+NP),N是人數,M是限制數量,P是排法數量。
由於PQ tree非常噁心,這裡不再多提,有興趣的讀者請自行搜尋資料。
ICPC 3511 UVa 11993
consecutive ones submatrix problem
NP-hard。
Gray code
Gray code
「格雷碼」。一串數列,0到2ᴺ - 1的整數各出現一次,表示成二進位。相鄰數字恰有一個位數不同,可能是1變0、0變1。數列頭尾視作相鄰。符合條件的數列,通常有許多種。
[N = 0] 0 [N = 1] 0 1 [N = 2] 00 01 11 10 [N = 3] 000 001 011 010 110 111 101 100
N維空間,正N方體,邊長為1,靠在原點上,貼齊座標軸,置於第一象限。任選一個頂點開始,沿邊行走,經過每個頂點各一次,走完一圈回到起點。途經座標就是一組Gray code!
011 111 011________ 111
/| /| / |
001 / | 101/ | 001/_______ |
| |_____|_|110 010______|_|110
| 010 | / |
000|________|100 000/_______|100
Gray code的遞推與遞歸
Gray code可以用遞推法解釋:
GrayCode(n-1)的每個數字,最高位數添0。 GrayCode(n-1)的每個數字,頭尾顛倒,最高位數添1。 兩者銜接起來就是GrayCode(n)。
Gray code可以用遞歸法解釋:
GrayCode(n)的每個數字,分成兩類。 第一類最高位數是0,拿掉最高位數即是GrayCode(n-1)。 第二類最高位數是1,拿掉最高位數即是GrayCode(n-1)。
也可以用最低位數為主,得到順序不同的Gray code。
生成Gray code
偶數項數字,由上一個數字,改變最低位的1的更高位數而得;奇數項數字,由上一個數字,改變最低位數而得。
不知如何解釋的方法。
Gray code的應用
tower of Hanoi河內塔的解法順序就是Gray code!
Chinese ring puzzle九連環的解法順序就是Gray code!
UVa 10455 11535
推廣到高維度
Gray code可以推廣到高維度。比方說二維的情況下,Gray code是一個方陣,上下左右皆循環,四方向相鄰數字恰有一個位數不相同。符合條件的方陣,通常有許多種。
[N = 0] 0
[N = 1] 0 1
1 0
[N = 2] 00 01 11 10
01 11 10 00
11 10 00 01
10 00 01 11
combination
combination(subset)
數學名詞「combination」,英文口語「selection」。
「組合」。意義等同「子集合」。
一堆東西,挑出其中幾個。可以全部都挑,也可以什麼都不挑。
組合就是挑選。組合就是剔除。無關順序。
例如有五筆資料 ●★■▲◆ 這是其中一種組合 ★■◆ 這和方才是同一種組合 ◆★■ 這是其中一種組合 ▲ 這是其中一種組合 ●★■▲◆ 這是其中一種組合 nothing
k-combination
挑出k個。
例如有五筆資料 ●★■▲◆ 取三筆資料的其中一種組合 ★■◆ 取三筆資料的其中一種組合 ●★■ 取三筆資料的其中一種組合 ■▲◆
編號所有組合
N筆資料的所有組合一共2ᴺ種。
一個二進位數字,可以代表一個子集合。
0 1 2 3 4
U = {lemon, orange, lime, apple, banana};
43210
二進位數字01010,即是子集合 {orange, apple}
二進位數字00001,即是子集合 {lemon}
二進位數字00000,即是子集合 { }
實作程式碼時,運用資料結構「bitset」或「整數」儲存一種組合,可以節省空間。運用程式語言的「bitwise operation」語法,可以節省時間。
枚舉所有組合
字典順序:數字由小到大。
000 001 010 011 100 101 110 111
Gray code:相鄰數字僅改動一個位元。
000 001 011 010 110 111 101 100
Banker's sequence:先枚舉小集合,再枚舉大集合;同樣大小的集合們之間,先枚舉數字大的(字典順序大的),再枚舉數字小的(字典順序小的)。
000 -- size = 0 100 \ 010 | size = 1 001 / 110 \ 101 | size = 2 011 / 111 -- size = 3
枚舉所有k組合
Gosper's hack:利用位元運算,快速得到下一個k組合。
00111 01011 01101 01110 10011 10101 10110 11001 11010 11100
luogu P1441
下一個k組合
給定其中一個組合,按照字典順序,找到下一個k組合。
不知名的方法:利用位元運算,快速得到下一個k組合。
inclusion–exclusion principle
inclusion–exclusion principle(PIE)
繁中「取捨原理」或「排容原理」、簡中「容斥原理」。
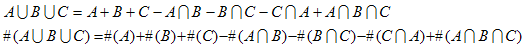
枚舉所有子集合,但是每個子集合有正負號之別──奇數個集合的交集是正號、偶數個集合的交集是負號。
範例:1到100當中不可被3或5或8整除的整數有幾個
3、5、8均兩兩互質。
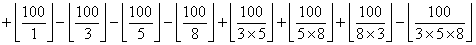
考慮數字之間不互質的情況。
另一種枚舉方式。
UVa 10325 11806 10458