backtracking

「回溯法」。枚舉多維度數值的方法。運用遞迴依序窮舉各個維度的數值，製作所有可能的多維度數值，並且在遞迴途中避免枚舉不正確的多維度數值。

int solution[MAX_DIMENSION]; // 多維度數值 void backtrack(int dimension) { /* prune：在遞迴途中避免枚舉不正確的多維度數值 */ if ( solution[] will not be an answer ) return; /* 製作了一組多維度數值，並檢驗正不正確 */ if ( dimension == MAX_DIMENSION ) { check and record solution[]; return; } /* 窮舉這個維度的所有數值，並遞迴到下一個維度 */ for ( x = possible value of current dimension ) { solution[dimension] = x; backtrack( dimension + 1 ); } } int main() { backtrack(0); // 從第一個維度開始枚舉 }

當多維度數值只需要唯一一組，可以讓程式提早結束。

int solution[MAX_DIMENSION]; bool find_answer = false; // 隨時記錄是否已經找到正解 void backtrack(int dimension) { if ( dimension == MAX_DIMENSION ) { check and record solution; find_answer = true; // 找到正解了 return; } for ( x = possible value of current dimension ) { solution[dimension] = x; backtrack( dimension + 1 ); if (find_answer) return; // 提早結束，跳出遞迴 } }

當多維度數值可以衡量優劣，就隨時剔除劣的、保留優的。

int solution[MAX_DIMENSION]; bool find_answer = false; int best_cost; // 用一數值代表多維度數值的優劣 void backtrack(int dimension) { /* bound：多維度數值太糟了，不可能成為正解，不必遞迴下去 */ int cost = cost of solution[]; // 計算優劣 if ( cost is far away from best_cost ) return; if ( dimension == MAX_DIMENSION ) { check and record solution[]; /* bound：多維度數值夠好了，可以成為正解，不必遞迴下去 */ best_cost = cost; // 記錄當前最佳結果 if ( cost is enough good ) find_answer = true; return; } for ( x = possible value of current dimension ) { solution[dimension] = x; backtrack( dimension + 1 ); if (find_answer) return; } }

回溯法的特色是隨時避免枚舉不正確的數值。一旦發現不正確的數值，就不遞迴至下一層，而是回溯至上一層，節省時間。

另外還可以調整維度先後順序、一個維度裡面的枚舉順序。如果安排得宜，可以更快找到正確的多維度數值。

UVa 140 165 193 222 259 291 301 331 399 435 524 539 565 574 598 628 656 732 10186 10344 10364 10400 10419 10447 10501 10503 10513 10582 10605 10624 10637 129 10160 10802

© 2010 tkcn. All rights reserved.

tuple

「元組」。意義是「多維度的元件組」。元件通常是數字。

例如數字1、2、3構成的三維數組是{1,1,1}、{1,1,2}、{1,1,3}、{1,2,1}、{1,2,2}、{1,2,3}、……、{3,3,2}、{3,3,3}。

範例：枚舉「數字1到10選擇五次」全部可能的情形

製作一個陣列，用來存放其中一個答案。陣列中不同的格子，就是不同的維度。

int solution[5];

例如solution[0] = 4表示第一個抓到的數字是4，solution[4] = 9表示第五個抓到的數字是9。

int solution[5]; // 用來存放其中一個答案 void print_solution() // 印出其中一個答案 { for (int i=0; i<5; i++) cout << i << ' '; cout << endl; } void backtrack(int n) // n是現在正在枚舉的維度 { // 製作了其中一個答案 if (n == 5) { print_solution(); return; } // 逐步枚舉數字1到10，並且遞迴下去，繼續枚舉之後的維度。 solution[n] = 1; backtrack(n+1); solution[n] = 2; backtrack(n+1); ...... solution[n] = 10; backtrack(n+1); } void enumerate_tuples() { backtrack(0); }

一般來說，重複很多次的程式碼，都會用迴圈進行簡化。

void backtrack(int n) // n是現在正在枚舉的維度 { // 製作了其中一個答案 if (n == 5) { print_solution(); return; } // 逐步枚舉數字1到10，並且遞迴下去，繼續枚舉之後的維度。 for (int i=1; i<=10; ++i) { solution[n] = i; backtrack(n+1); } }

permutation

便是數學課本中「排列組合」的「排列」。但是這裡不是要計算排列有多少種，而是枚舉所有的排列，以字典順序枚舉。

例如{1,2,3}所有的排列就是{1,2,3}、{1,3,2}、{2,1,3}、{2,3,1}、{3,1,2}、{3,2,1}。

範例：枚舉{0,1,2,3,4}所有排列

依序枚舉每個位置。針對每個位置，試著填入各種數字。

int solution[5]; // 用來存放其中一個答案 bool used[5]; // 記錄數字是否使用過，用過是true。 void backtrack(int n) { // 製作了其中一個答案 if (n == 5) { // 印出其中一個答案 for (int i=0; i<5; i++) cout << solution[i] << ' '; cout << endl; return; } // 逐步枚舉數字0到4，並且遞迴下去，繼續枚舉之後的維度。 if (!used[0]) // 用過的數字不能再用 { used[0] = true; // 記錄用過的數字 solution[n] = 0; // 第 n 格填入數字 0 backtrack(n+1); // 繼續枚舉之後的維度 used[0] = false; // 回收用完的數字 } if (!used[1]) { used[1] = true; solution[n] = 1; backtrack(n+1); used[1] = false; } ...... if (!used[4]) { used[4] = true; solution[n] = 4; backtrack(n+1); used[4] = false; } } void enumerate_permutations() { for (int i=0; i<5; i++) // 一開始所有數字皆未使用 used[i] = false; backtrack(0); // 印出數字0到4的所有排列。 }

一般來說，重複很多次的程式碼，都會用迴圈進行簡化。

void backtrack(int n) { // 製作了其中一個答案 if (n == 5) { for (int i=0; i<5; i++) cout << solution[i] << ' '; cout << endl; return; } // 寫成一個迴圈 for (int i=0; i<5; i++) if (!used[i]) { used[i] = true; solution[n] = i; backtrack(n+1); used[i] = false; } }

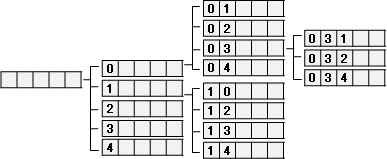
範例：枚舉{0,1,2,3,4}所有排列

依序枚舉每個數字。針對每個數字，試著填入各個位置。

int solution[5]; // 用來存放其中一個答案 bool filled[5]; // 記錄各個位置是否填過數字，填過是true。 void backtrack(int n) { // 製作了其中一個答案 if (n == 5) { for (int i=0; i<5; i++) cout << solution[i] << ' '; cout << endl; return; } for (int i=0; i<5; i++) // 試著將數字 n 填入各個位置 if (!filled[i]) { filled[i] = true; // 記錄填過的位置 solution[i] = n; // 將數字 n 填入第 i 格 backtrack(n+1); // 繼續枚舉下一個數字 filled[i] = false; // 回收位置 } } void enumerate_permutations() { for (int i=0; i<5; i++) // 一開始所有位置皆未填過 filled[i] = false; backtrack(0); // 印出數字1到5的所有排列。 }

範例：枚舉{1,2,5,8,9}所有排列

特地建立一個集合，儲存這些沒有特殊規則的數字。

預先排序數字，輸出結果就會照字典順序排列。

int s[5] = {1, 2, 5, 8, 9}; // 集合 int solution[5]; // 用來存放其中一個答案 bool used[5]; // 記錄該數字是否使用過，用過為true。 void backtrack(int n) { // 製作了其中一個答案 if (n == 5) { for (int i=0; i<5; i++) cout << solution[i] << ' '; cout << endl; return; } // 針對solution[i]這個位置，枚舉所有數字，並各自遞迴。 for (int i=0; i<5; i++) if (!used[i]) { used[i] = true; solution[n] = s[i]; // 填入數字 backtrack(n+1); used[i] = false; } } void enumerate_permutations() { for (int i=0; i<5; i++) // 一開始所有數字皆未使用 used[i] = false; backtrack(0); // 印出數字1 2 5 8 9的所有排列 }

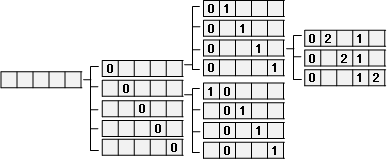
範例：枚舉{0,1,1}所有排列，避免重複排列。

答案應該是{0,1,1}、{1,0,1}、{1,1,0}。然而使用剛剛的程式碼，答案卻是這樣：

{0,1,1}
{0,1,1}
{1,0,1}
{1,1,0}
{1,0,1}
{1,1,0}

出現了重複排列，跟預期結果不一樣。原因是剛剛的程式碼有個基本假設：每個數字都不一樣。

想要避免重複排列，就要避免在一樣的位置重複填入一樣的數字。將數字由小到大排序，讓數字依照大小順序出現；然後檢查方才填入的數字，判斷一不一樣，就可以避免填入一樣的數字了。

int s[3] = {0, 1, 1}; // 集合，必須預先由小到大排序。 int solution[3]; bool used[3]; void backtrack(int n) { if (n == 3) { for (int i=0; i<3; i++) cout << solution[i] << ' '; cout << endl; return; } int last_number = -1; for (int i=0; i<3; i++) if (!used[i]) if (s[i] != last_number) // 避免枚舉一樣的數字 { last_number = s[i]; // 記錄方才填入的數字 used[i] = true; solution[n] = s[i]; backtrack(n+1); used[i] = false; } } int s[3] = {0, 1, 1}; // 集合，必須預先由小到大排序。 int solution[3]; bool used[3]; void backtrack(int n) { if (n == 3) { for (int i=0; i<3; i++) cout << solution[i] << ' '; cout << endl; return; } int last_number = -1; for (int i=0; i<3; i++) { // if not 改成 continue if (used[i]) continue; if (s[i] == last_number) continue; last_number = s[i]; used[i] = true; solution[n] = s[i]; backtrack(n+1); used[i] = false; } }

範例：枚舉{0,0,0,1,1,1,1}所有排列，避免重複排列。

如果有許多重覆的數字，此時可以使用一條陣列，每一格分別存入每一種數字的出現次數，簡化程式碼。

int s[7] = {0, 0, 0, 1, 1, 1, 1}; int count[2]; // 每一格分別存入每一種數字的出現次數 int solution[7]; void backtrack(int n) { if (n == 7) { for (int i=0; i<7; i++) cout << solution[i] << ' '; cout << endl; return; } for (int i=0; i<2; i++) // 枚舉每一種數字 if (count[i] > 0) // 還有數字剩下來，就要枚舉 { count[i]--; // 用掉了一個數字 solution[n] = i; // 第 n 格填入數字 i backtrack(n+1); // 繼續枚舉之後的維度 count[i]++; // 回收了一個數字 } } void enumerate_permutations() { // 一開始所有數字皆未使用 for (int i=0; i<2; i++) count[i] = 0; for (int i=0; i<2; i++) count[s[i]]++; backtrack(0); // 印出數字0 0 0 1 1 1 1的所有排列 }

UVa 195 441 10098 10063 10776

combination（subset）

便是數學課本中「排列組合」的「組合」；概念等於「子集合」。但是這裡不是要計算組合有多少種，而是枚舉所有的組合，以字典順序枚舉。

例如{1,2,3}所有的組合就是{}、{1}、{2}、{3}、{1,2}、{1,3}、{2,3}、{1,2,3}。

範例：枚舉{0,1,2,3,4}所有組合

該如何枚舉呢？先觀察平時我們計算組合個數的方法。

{0,1,2,3,4}所有組合個數總共2⁵個：0可取可不取，有兩種情形、1可取可不取，有兩種情形、...、4可取可不取，有兩種情形。根據乘法原理，總共2×2×2×2×2 = 2⁵種情形。

枚舉方式可以仿照乘法原理。建立一個陣列，當作一個集合。solution[i] = true表示這個集合擁有第i個元素，觀念等同「Set資料結構: 索引儲存」。

依序枚舉每個位置。針對每個位置，試著填入取或不取。

bool solution[5]; // 索引儲存 void backtrack(int n) { // 製作了其中一個答案 if (n == 5) { for (int i=0; i<5; i++) if (solution[i]) cout << i << ' '; cout << endl; return; } // 選取數字n，然後繼續枚舉之後的位置。 solution[n] = true; backtrack(n+1); // 不取數字n，然後繼續枚舉之後的位置。 solution[n] = false; backtrack(n+1); } void enumerate_combinations() { backtrack(0); }

亦得改用其他資料結構，例如「Set資料結構: 循序儲存」。

int subset[5]; // 循序儲存 void backtrack(int n, int size) // size是子集合大小 { // 製作了其中一個答案 if (n == 5) { // print solution for (int i=0; i<size; i++) cout << subset[i] << ' '; cout << endl; return; } // 選取數字n，然後繼續枚舉剩下的數字。 subset[size] = n; backtrack(n+1, size+1); // 不取數字n，然後繼續枚舉剩下的數字。 backtrack(n+1, size); } void enumerate_combinations() { backtrack(0, 0); }

範例：枚舉{0,1,2,3,4}所有組合

依序枚舉每個選取。針對每個選取，試著填入各個位置。

bool solution[5]; // 索引儲存 void backtrack(int n) { // print_solution for (int i=0; i<5; i++) if (solution[i]) cout << i << ' '; cout << endl; for (; n<5; ++n) { // 選取數字n solution[n] = true; // 然後繼續枚舉後面的數字 backtrack(n+1); // 回復原狀 solution[n] = false; } } void enumerate_combinations() { backtrack(0); } int subset[5]; // 循序儲存 void backtrack(int n, int size) // size是子集合大小 { // print_solution for (int i=0; i<size; i++) cout << subset[i] << ' '; cout << endl; for (; n<5; ++n) { // 選取數字n subset[size] = n; // 然後繼續枚舉後面的數字 backtrack(n+1, size+1); // 不必特地回復原狀，數字n會覆蓋過去。 } } void enumerate_combinations() { backtrack(0, 0); }

範例：枚舉{6,7,9,4,2}所有組合

特地建立一個集合，儲存這些沒有特殊規則的數字。

預先排序數字，輸出結果就會照字典順序排列。

int array[5] = {6, 7, 9, 4, 2}; int subset[5]; // 循序儲存 void backtrack(int n, int size) // size是子集合大小 { // 製作了其中一個答案 if (n == 5) { print_solution(); return; } // 選取數字array[n]，然後繼續枚舉剩下的數字。 subset[size] = array[n]; backtrack(n+1, size+1); // 不取數字array[n]，然後繼續枚舉剩下的數字。 backtrack(n+1, size); } void enumerate_combinations() { sort(array, array+5); backtrack(0, 0); } int array[5] = {6, 7, 9, 4, 2}; int subset[5]; // 循序儲存 void backtrack(int n, int size) // size是子集合大小 { print_solution(); for (; n<5; ++n) { // 選取數字array[n] subset[size] = array[n]; // 然後繼續枚舉剩下的數字 backtrack(n+1, size+1); } } void enumerate_combinations() { sort(array, array+5); backtrack(0, 0); }

subset sum

例如{1,2,8}所有的子集和就是0、1、2、8、1+2、1+8、2+8、1+2+8。

直覺的解法是枚舉所有子集合，分別求總和，最後再排序。

可以直接由小到大枚舉嗎？可以！運用即時排序資料結構，調整回溯法的枚舉順序。每個數字都有「取」和「不取」兩種選擇，放入即時排序資料結構，由即時排序資料結構決定下一個枚舉的對象。

簡單起見，假設數字都是正數。首先是簡單的做法，但是有錯誤，出現多餘的零。

const int N = 5; // 集合大小 const int K = 6; // 枚舉前6名子集和 int array[N] = {2, 4, 6, 7, 9}; // 集合，預先由小到大排序 struct Pair {int n, num;}; // C++標準函式庫的priority_queue，排序結果由大到小。 // 因此比大小時要顛倒，排序結果才會由小到大。 bool operator<(Pair a, Pair b) { return a.num > b.num; } void enumerate_subset_sums() { // 從空集合開始實施回溯法 priority_queue<Pair> pq; pq.push({0, 0}); for (int k=0; k<K; k++) { // 找到當前最小的子集和 if (pq.empty()) break; int n = pq.top().n; int num = pq.top().num; pq.pop(); cout << num; // 遞迴到下一個維度 if (n < N) { pq.push({n+1, num + array[n]}); // 取 pq.push({n+1, num}); // 不取 } } }

再來是正確的做法。稍作改良，避免多餘的零。

const int N = 5; const int K = 6; int array[N] = {2, 4, 6, 7, 9}; struct Pair {int n, num;}; bool operator<(Pair a, Pair b) { return a.num > b.num; } void enumerate_subset_sums() { cout << 0; // 預先補入一個數，稍後再扣除回來。 priority_queue<Pair> pq; pq.push({0, array[0]}); for (int k=1; k<K; k++) { if (pq.empty()) break; int n = pq.top().n; int num = pq.top().num; pq.pop(); cout << num; if (n + 1 < N) { // 取 pq.push({n+1, num + array[n+1]}); // 不取 pq.push({n+1, num - array[n] + array[n+1]}); } } }

八皇后問題

問題：在8x8的西洋棋棋盤上擺放八隻皇后，讓他們恰好無法互相攻擊對方。皇后的攻擊範圍是米字。

一個非常簡單的想法：每一格都有「放」和「不放」兩種選擇，枚舉所有可能，並避免枚舉皇后互相攻擊的情形。建立8x8的bool陣列，代表一個8x8的棋盤盤面情形。例如solution[0][0] = true表示(0,0)這個位置有放置皇后。

bool solution[8][8]; void backtrack(int x, int y) { if (y == 8) x++, y = 0; // 換到下一排格子 // 製作了其中一個答案 if (x == 8) { print_solution(); return; } // 放置皇后 solution[x][y] = true; backtrack(x, y+1); // 不放置皇后 solution[x][y] = false; backtrack(x, y+1); } void eight_queen() { backtrack(0, 0); }

接著要避免枚舉不可能出現的答案：任一直線、橫線、左右斜線上面只能有一隻皇后。分別建立四個bool陣列，記錄皇后在各條線上擺放的情形。

bool solution[8][8]; bool mx[8], my[8], md1[15], md2[15]; // 初始值都是 false void backtrack(int x, int y) { if (y == 8) x++, y = 0; // 換到下一排格子 // 製作了其中一個答案 if (x == 8) { print_solution(); return; } // 放置皇后 int d1 = (x+y) % 15, d2 = (x-y+15) % 15; if (!mx[x] && !my[y] && !md1[d1] && !md2[d2]) { // 這隻皇后佔據了四條線，記得標記起來。 mx[x] = my[y] = md1[d1] = md2[d2] = true; solution[x][y] = true; backtrack(x, y+1); // 遞迴結束，回復到原本的樣子，要記得取消標記。 mx[x] = my[y] = md1[d1] = md2[d2] = false; } // 不放置皇后 solution[x][y] = false; backtrack(x, y+1); } void eight_queen() { backtrack(0, 0); }

以及避免枚舉不可能出現的答案：最終的棋盤上面不足八隻皇后。

bool solution[8][8]; bool mx[8], my[8], md1[15], md2[15]; // 初始值都是 false void backtrack(int x, int y, int c) { if (y == 8) x++, y = 0; // 換到下一排格子 // 製作了其中一個答案 if (x == 8) { if (c != 8) return; // 不是八隻皇后就避免枚舉答案 print_solution(); return; } // 放置皇后 int d1 = (x+y) % 15, d2 = (x-y+15) % 15; if (!mx[x] && !my[y] && !md1[d1] && !md2[d2]) { mx[x] = my[y] = md1[d1] = md2[d2] = true; solution[x][y] = true; backtrack(x, y+1, c+1); // 皇后多一隻 mx[x] = my[y] = md1[d1] = md2[d2] = false; } // 不放置皇后 solution[x][y] = false; backtrack(x, y+1, c); // 皇后和原來一樣多 } void eight_queen() { backtrack(0, 0, 0); // 一開始棋盤是空的，皇后數目是零。 }

改進

由於一條線必須剛好擺放一隻皇后，故可以以線為單位來遞迴窮舉。重新建立一條一維int陣列，solution[0] = 5表示第零個直行上的皇后，擺在第五個位置。

int solution[8]; void backtrack(int x) // 每次都換一排格子 { // 製作了其中一個答案 if (x == 8) { print_solution(); return; } // 分別放置皇后在每一格，並各自遞迴下去。 solution[x] = 0; backtrack(x+1); solution[x] = 1; backtrack(x+1); ...... solution[x] = 7; backtrack(x+1); }

縮成迴圈是一定要的啦！

int solution[8]; void backtrack(int x) // 每次都換一排格子 { // 製作了其中一個答案 if (x == 8) { print_solution(); return; } // 分別放置皇后在每一格，並各自遞迴下去。 for (int y=0; y<8; ++y) { solution[x] = y; backtrack(x+1); } }

接著要避免枚舉不可能出現的答案。

int solution[8]; bool my[8], md1[15], md2[15]; // 初始值都是 false // x這條線可以不用檢查了 void backtrack(int x) // 每次都換一排格子 { // 製作了其中一個答案 if (x == 8) { print_solution(); return; } // 分別放置皇后在每一格，並各自遞迴下去。 for (int y=0; y<8; ++y) { int d1 = (x+y) % 15, d2 = (x-y+15) % 15; if (!my[y] && !md1[d1] && !md2[d2]) { // 這隻皇后佔據了四條線，記得標記起來。 my[y] = md1[d1] = md2[d2] = true; solution[x] = y; backtrack(x+1); // 遞迴結束，回復到原本的樣子，要記得取消標記。 my[y] = md1[d1] = md2[d2] = false; } } }

改進

8 queen problem的答案是上下、左右、對角線對稱的。排除對稱的情形，可以節省枚舉的時間。這裡不加贅述。

另一種左右斜線判斷方式

比用陣列記錄還麻煩。自行斟酌。

void backtrack(int x) // 每次都換一排格子 { for (int i=0; i<x; ++i) if (abs(x - i) == abs(solution[x] - solution[i])) return; ...... }

UVa 167 750 10513 639 989 10893 10957

0/1背包問題

問題：各式各樣的物品，重量與價值皆異。一個背包，具有耐重限制。現在將物品儘量塞入背包，令背包裡物品總價值最高。

一個簡單的想法：每個物品都有「要」和「不要」兩種選擇，窮舉所有可能，並避免枚舉背包超載的情形。建立一維bool陣列，solution[0] = true表示第零個物品有放進背包。

bool solution[10]; // 十個物品 int weight[10] = {4, 54, 1, ..., 32}; // 十個物品分別的重量 int cost[10] = {3, 3, 11, ..., 23}; // 十個物品分別的價值 const int maxW = 100; // 背包承載上限 int maxC = 0; // 出現過的最高總值 void backtrack(int n, int w, int c) { // 製作了其中一個答案 if (n == 10) { if (c > maxC) // 記錄總值最高的 { maxC = c; save_solution(); } return; } // 放進背包 if (w + weight[n] <= maxW) // 檢查背包超載 { solution[n] = true; backtrack(n+1, w + weight[n], c + cost[n]); } // 不放進背包 solution[n] = false; backtrack(n+1, w, c); } bool answer[10]; // 正確答案 void store_solution() { for (int i=0; i<10; ++i) answer[i] = solution[i]; }

檢查背包超載的部分可以修改成更美觀的樣子。

void backtrack(int n, int w, int c) { if (w > maxW) return; // 背包超載 // 製作了其中一個答案 if (n == 10) { if (c > maxC) // 記錄總值最高的 { maxC = c; store_solution(); } return; } // 放進背包 solution[n] = true; backtrack(n+1, w + weight[n], c + cost[n]); // 不放進背包 solution[n] = false; backtrack(n+1, w, c); }

各位可以預先排序物品重量，再執行程式，看看效率有何不同。然後嘗試使用heuristic bound加快速度。

© 2010 tkcn. All rights reserved.

二維座標平面，兩點之間的最短路徑

在一張地圖上有很多個地點，鄰近的地點有筆直道路相通，我們也知道每一段道路的長度。現在要沿著道路，從一個地點走到另一個地點，請問要怎麼走距離最短呢？

一條最短的路徑，肯定不會繞圈子。我們可以窮舉所有排列，製造所有可能的路徑。每當生成一條路徑，就判斷這條路徑是不是歷來最短的路徑，並且隨時記得歷來最短的路徑。

struct Point {double x, y;} p[10]; // 所有地點的座標， // 編號是0到9。 bool connect[10][10]; // 兩個地點之間是否有筆直道路相通 // 若相通是true，不相通是false。 int s = 0, t = 9; // 起點與終點的編號 int solution[10]; // 一條可能的路徑 bool used[10]; // 記錄數字是否使用過，用過是true。 int best_solution[10]; // 隨時記得歷來最短的路徑 int best_dist; // 隨時記得歷來最短的路徑的長度 // 計算兩點之間的直線距離 double length(Point a, Point b) { double dx = b.x - a.x, dy = b.y - a.y; return sqrt(dx * dx + dy * dy); } void backtrack(int n, int a, int dist) { // prune，生成不合理的解答就馬上回溯。 if (n > 2 && !connect[solution[n-2]][solution[n-1]]) return; // 製作了其中一個答案 if (a == t) { // 記錄歷來最短的路徑 if (dist < best_dist) { best_dist = dist; for (int i=0; i<n; ++i) best_solution[i] = solution[i]; } return; } // 窮舉所有排列 for (int b=0; b<10; ++b) if (!used[b]) { used[b] = true; solution[n] = b; backtrack(n+1, b, dist + length(p[a], p[b]); used[b] = false; } } void Euclidean_shortest_path() { best_dist = 1e9; // 設定為很大的數值，代表無限遠。 used[s] = true; // 設定好起步起點 solution[0] = s; backtrack(0+1, 0, 0); }

prune的程式碼，可以放在遞迴函式一開始的地方，也可以放在遞迴函式呼叫的前一刻。視情況選用直觀易懂的寫法。

void backtrack(int n, int a, int dist) { // 製作了其中一個答案 if (a == t) { // 記錄歷來最短的路徑 if (dist < best_dist) { best_dist = dist; for (int i=0; i<n; ++i) best_solution[i] = solution[i]; } return; } // 窮舉所有排列 for (int b=0; b<10; ++b) if (connect[a][b]) // prune，有路才能通行。 if (!used[b]) { used[b] = true; solution[n] = b; backtrack(n+1, b, dist + length(p[a], p[b]); used[b] = false; } }

很多人誤認backtracking就是圖論的DFS，然而兩者沒有關係。兩者相似的地方是：backtracking遇到不合理的解答會馬上回溯，DFS遇到拜訪過的節點會馬上回溯。

bounding

遞迴過程中，如果當下產生的路徑片段，已經超過歷來最短的路徑長度，則可以馬上回溯。堅持遞迴下去，路徑片段只會越變越長，將來仍然是超過歷來最短的路徑長度，根本不可能構成正確解答──不如當下就回溯，及早發現及早治療。

void backtrack(int n, int a, int dist) { // bound // 路徑片段已經太長，窮舉下去沒有意義了，可以馬上回溯。 if (dist >= best_dist) return; ...... }

heuristic bounding

遞迴過程中，如果當下產生的片段路徑，我們預測它延伸到終點之後，鐵定超過歷來最短的路徑長度，則可以馬上回溯。先知先覺，防範未然，少走許多冤枉路。

void backtrack(int n, int a, int dist) { // heuristic bound // 還沒到之前，如果發現已經太遠了，就不繼續走，改換條路。 if (dist + length(p[a], p[t]) >= best_dist) return; ...... }

這個問題可以套用最短路徑演算法，甚至可以使用A*、IDA*解決。不過這已經超出回溯法的範圍了。