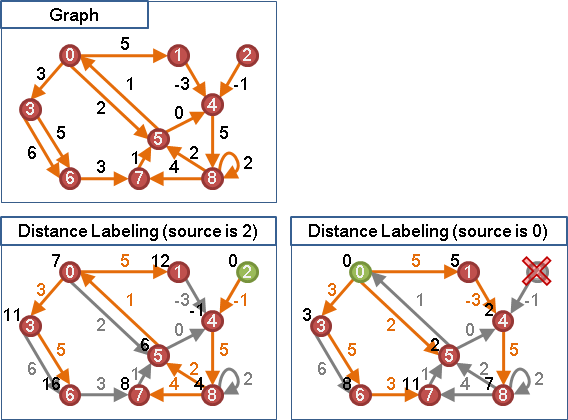
all pairs shortest paths: Johnson's algorithm
用途
一張有向圖,找出所有兩點之間的最短路徑。
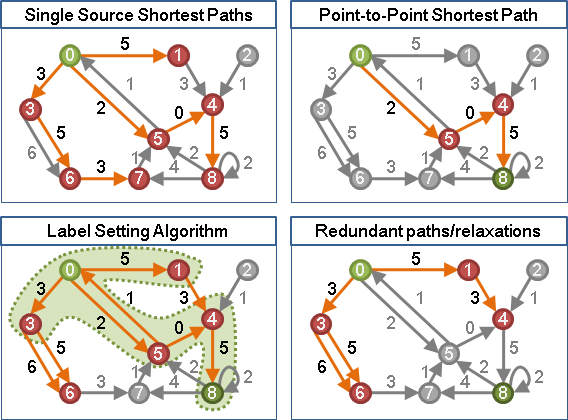
首先重新調整邊的權重為非負數,順便檢查圖上是否有負環。接著放心使用label setting algorithm計算所有兩點之間的最短路徑。
重新調整權重
如何調整權重,才不會影響最短路徑、負環的位置呢?
這裡介紹一個巧妙的方法:首先圖上每一個x點都設定一個權重h(x),然後將一條由i點到j點的邊的權重w(i,j),重新調整成w'(i,j) = w(i,j) + h(i) - h(j)。
一、一條路徑s⤳t,權重變成了:
w'(s⤳t) = w'(s→a→b→…→z→t) = w'(s,a) + w'(a,b) + … + w'(z,t) = [ w(s,a)+h(s)-h(a) ] + [ w(a,b)+h(a)-h(b) ] + … + [ w(z,t)+h(z)-h(t) ] = w(s,a) + w(a,b) + … + w(z,t) + h(s) - h(t) = w(s→a→b→…→z→t) + h(s) - h(t) = w(s⤳t) + h(s) - h(t)
一加一減相消,得到簡潔的結果。
h(s)和h(t)都是定值。由s點到t點的每一條路徑,權重的變動量都一樣,權重大小關係保持不變,於是乎由s點到t點的最短路徑保持不變。圖上的最短路徑,調整權重之後,依然保持不變。
二、一個環s⤳s,權重變成了:
w'(s⤳s) = w'(s→a→b→…→s) = w(s→a→b→…→s) + h(s) - h(s) = w(s⤳s)
環的權重保持不變,於是乎由s點到s點的負環保持不變。圖上的負環,調整權重之後,依然保持不變。
重新調整權重為非負數:利用單源最短路徑長度
調整權重而不會影響最短路徑和負環的方法已經有了。現在要妥善設定h(x)的值,讓每一條邊的權重都調整為非負數。
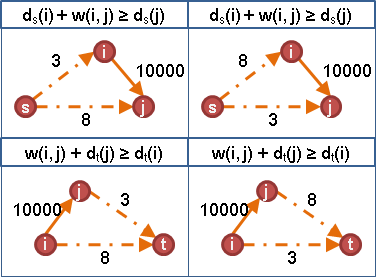
找到最短路徑樹之後,圖上每一條邊都不可能再做relaxation,數學式子d(i) + w(i,j) ≥ d(j),移項w(i,j) + d(i) - d(j) ≥ 0,正好就是調整權重的式子。
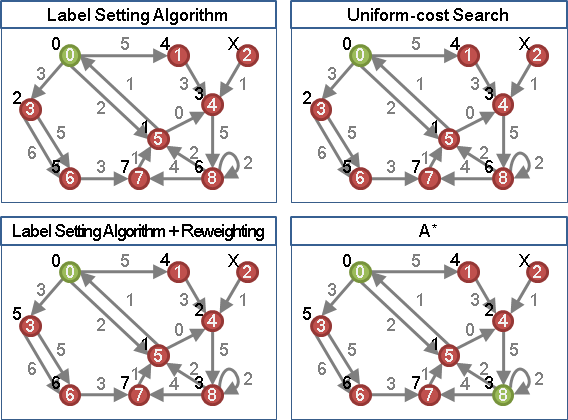
因此,令h(x)是由一個起點到各個x點的最短路徑長度,就能重新調整權重為非負數;無論起點是哪一點,數學式子都會成立。
起點應該選誰呢?因為圖上每一條邊都必須調整權重、圖上每一個點都必須設定h(x)值,所以起點必須能夠到達圖上每一個點,如此圖上每一個點才有h(x)值。
巧妙的解決方式:增加一個超級起點,連向圖上每一個點,權重設定為零。
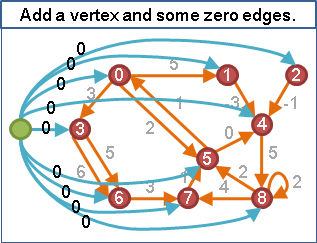
順帶一提,以單源最短路徑長度重新調整權重,所有最短路徑的所有邊,權重都會變成零。這是一個很好用的特性。
演算法
一、增加一個超級起點,連向原圖每一個點,權重設定為零。 二、以超級起點作為起點,實施label correcting algorithm。 甲、求得超級起點到原圖每一個點的最短路徑長度,作為h(x)。 乙、順便檢查原圖是否有負環。 三、調整原圖每一條邊(i,j)的權重: w'(i,j) = w(i,j) + h(i) - h(j) 四、原圖每一個點分別作為起點, 分別實施label setting algorithm with binary heap, 找出圖上任兩點之間的最短路徑。 五、找出最短路徑後,對照原圖求出正確的最短路徑長度。 或者利用h(x)逆推:w(s⤳t) = w'(s⤳t) - h(s) + h(t)。
時間複雜度
一次label correcting algorithm以及V次label setting algorithm with binary heap的時間。
圖的資料結構為adjacency lists是O(V² + VElogV)。當圖上的邊很少,比Floyd–Warshall algorithm來得快。