complete graph
complete graph
「完全圖」。任兩點都有一條邊。
連滿了邊，看起來相當堅固。
大家傾向討論無向圖，不討論有向圖。有向圖太複雜。
complete subgraph（clique）
「完全子圖」、「團」。子圖，而且任兩點都有一條邊。
極大團maximal clique：無法再添加點的團。可能有許多個。
最大團maximum clique：點最多的團。可能有許多個。
所有團當中，最大者，就是最大團。所有極大團當中，最大者，就是最大團。
minimal、maximal是局部極值，minimum、maximum是全域極值。遣詞用字請小心！
尋找最大團，NP-complete問題，沒有快速的演算法。
窮舉極大團，從中找出最大團，不失為一個務實的方法。
maximal clique enumeration: Bron–Kerbosch algorithm
maximal clique enumeration
R: 目前的clique。 P: 可以增大目前clique的點集合。接下來要列舉的點。 （與目前clique上所有點皆相鄰的點，構成的集合） X: 可以增大目前clique的點集合，但是先前已經列舉過。用來避免重複列舉。
此演算法採用backtracking。時間複雜度O(n⋅3ⁿ⸍³)。
選擇適當的pivot，讓各階段列舉的點都是最少，時間複雜度加速為O(3ⁿ⸍³)。
點的列舉順序採用degeneracy order，時間複雜度加速為O(d⋅n⋅3ᵈ⸍³)，d是原圖的degeneracy。
下面提供的實作是隨意選擇pivot，稍微減少列舉的點。
transitive graph
transitive graph
「遞移圖」。凡有路、必有邊。
連通關係的完全圖。
大家傾向討論有向圖，不討論無向圖。無向圖太簡單。
transitive subgraph
「遞移子圖」。子圖，而且凡有路、必有邊。
尋找最大遞移子圖，NP-complete問題，沒有快速的演算法。
列舉遞移子圖的演算法，我沒有研究。
transitive closure
「遞移閉包」其實是一種變換的概念，可以看做是一個函數。
一張圖的「遞移閉包」也是一張圖。記錄由一點能不能走到另一點。如果能走到，則兩點之間以邊相連。
「遞移閉包」。添加邊，連通關係保持相同，並且形成遞移圖。
每個點分別作為起點，實施遍歷。總共遍歷V次。時間複雜度O((V+E) ⋅ V) = O(V² + VE)，通常簡單寫成O(VE)。
transitively equivalent graph
「遞移相等圖」。子圖，而且擁有相同的遞移閉包。
「遞移相等圖」。刪除邊，連通關係保持相同。
最小相等圖minimum equivalent graph：保留盡量少的邊、刪除盡量多的邊。
尋找最小相等圖，NP-complete問題，沒有快速的演算法。
transitive reduction
「遞移縮減」。另外一張圖，恰好擁有相同的遞移閉包。
遞移縮減、遞移相等圖，名不符實、意義顛倒。古人腦殘。
最小遞移縮減minimum transitive reduction：邊盡量少。
無向圖：生成森林。可能有許多種。總共遍歷1次。
有向圖：NP-hard。
有向無環圖：所有點對的最長路徑，保留長度是1的最長路徑（只有一條邊）。只有唯一一種。總共遍歷V次。
有向無環圖的情況下，遞移相等圖、遞移縮減，兩者恰好相等。這可能是古人將兩者搞混的原因。
transitive closure: Purdom's algorithm
演算法
強連通分量的遞移閉包是團，不必特地計算。收縮所有的強連通分量SCC，變成有向無環圖DAG。
觀察有向無環圖的拓樸順序，所有路徑都是從順序小的點走往順序大的點。一邊建立拓樸順序，一邊檢查是否連通，一邊添加邊以形成遞移閉包。
最多添加1+2+...+(K-1) = K(K-1)/2 = O(K²)條邊。K是新圖的點數量、原圖的SCC數量。時間複雜度O(V+E+K²)。
transitive closure: Warshall's algorithm
演算法
雖然時間複雜度較高，但是很有特色的演算法。
dynamic programming。取出第k點，分成兩種情況，遞迴分割問題。
tc(i, j, k) = tc(i, k, k-1) && tc(k, j, k-1) || tc(i, j, k-1)
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^
經過第k點 沒有經過第k點
tc(i, j, k)：由i點能不能走到j點。中繼點只能是第0點到第k點。
時間複雜度O(V³)，空間複雜度O(V²)。
UVa 280 12017
comparability graph
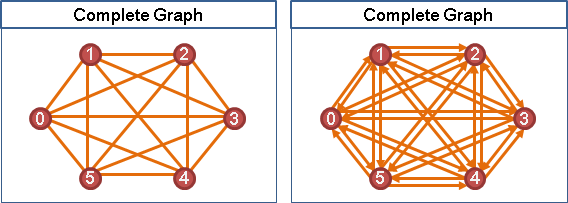
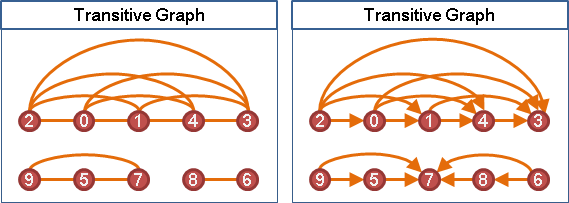
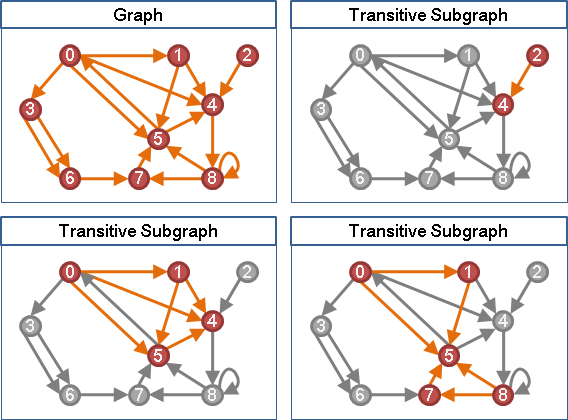
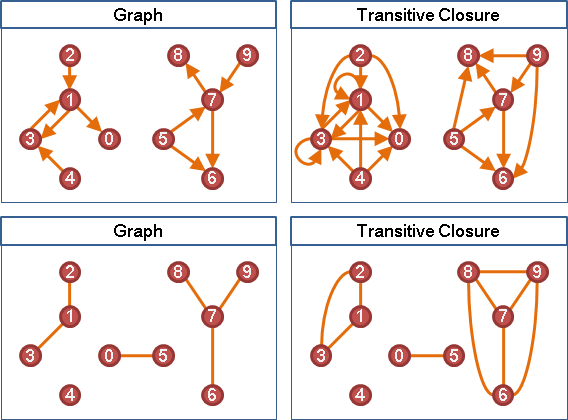
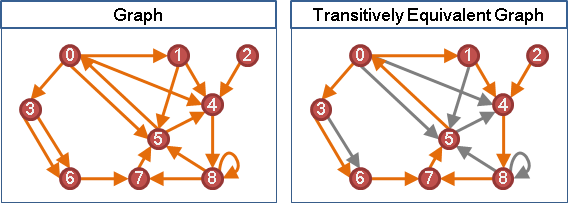
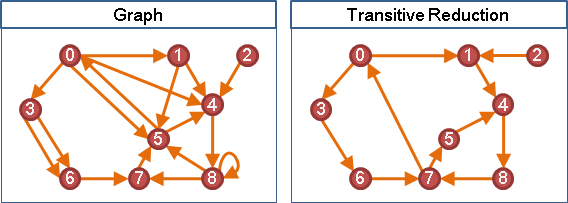
comparability graph（transitively orientable graph）
「可比圖」源自集合論的「偏序集poset」，但是不盡相同。
DAG的transitive closure的underlying graph。
Mirsky's theorem / Dilworth's theorem
有向無環圖DAG有兩個特殊性質，在可比圖才有顯著功用，因而挪到此處介紹。
chain：一群點，一條路徑的所有點。 anti-chain：一群點，任兩點正向不連通、逆向也不連通。
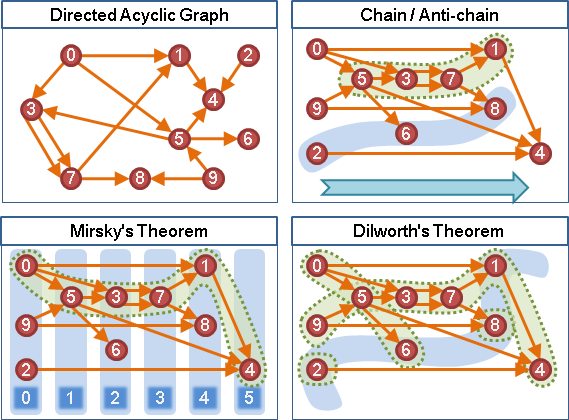
maximum chain length = minimum anti-chain cover [depth] [level]
(≥) 一個level使用一條anti-chain。
(≤) 一條anti-chain不可以經過同一條chain上的點。
一條chain，每一個點至少需要一條anti-chain。
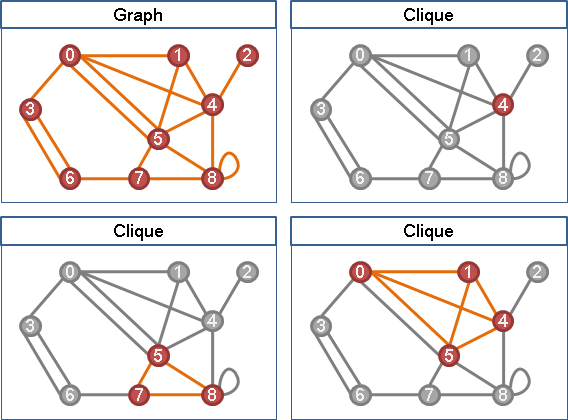
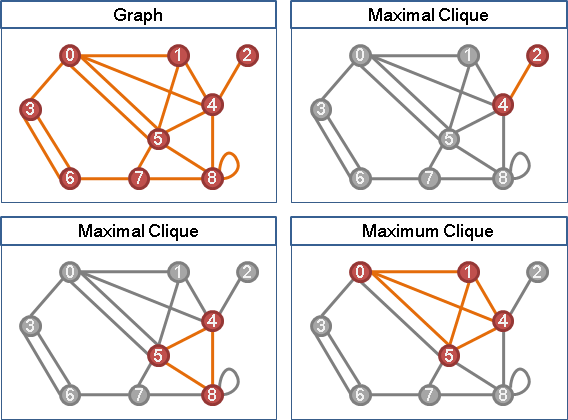
實際應用，例如可比圖的minimum vertex coloring：簡圖的一條路徑，經由transitive closure，其實是原圖的一個團──所有點互相連通，每一點顏色必須不同。因此簡圖的最長路徑的長度，就是原圖的最小點著色的大小。
minimum chain cover = maximum anti-chain length [number of paths] [cross all paths]
實際應用，例如可比圖的maximum independent set：簡圖的一條路徑，經由transitive closure，其實是原圖的一個團──只夠塞入一點，塞入兩點就相鄰。因此簡圖的最小路徑覆蓋的數量，就是原圖的最大獨立集的大小。
Greene–Kleitman theorem
Dilworth's theorem推廣版本。我沒有研究。