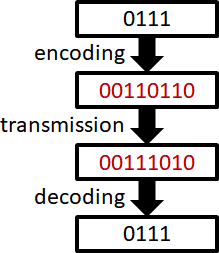
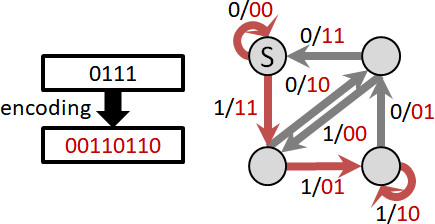
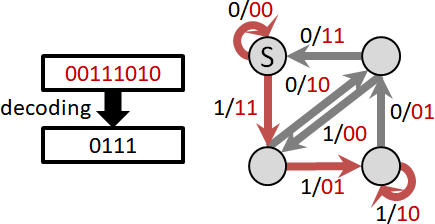
optimal path
optimal path
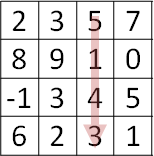
請找到上緣到下緣的最佳路線:數字總和最小的路線。
只能走往左下、下、右下(來自左上、上、右上)
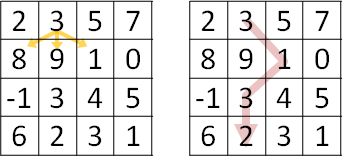
遇事不決,首先枚舉。
直覺的方式是回溯法。枚舉所有路線,從中找出最佳路線。
地圖的長寬是H和W。格子的數量是HW。路線的數量是W⋅3⋅3⋅...⋅3 = W⋅3ᴴ⁻¹再少一些,左緣與右緣只會衍生兩條路線。
時間複雜度O(W⋅3ᴴ⁻¹) = O(W⋅3ᴴ)。1/3是常數倍率,O()無視常數倍率。
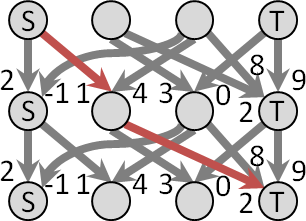
更好的方式是動態規劃。原問題,刪除下緣,形成子問題。
源頭的子問題:只剩上緣。
計算順序:從上往下,逐層計算。
時間複雜度O((HW)⋅3) = O(HW)。3是常數倍率,O()無視常數倍率。
UVa 116 10564
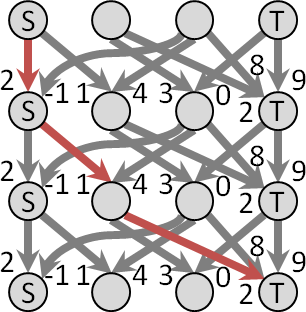
只能走往下一層任一格(來自上一層任一格)
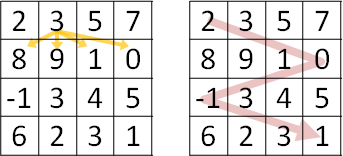
枚舉三格改成枚舉一層。
時間複雜度O((HW)⋅W)。
然而,上一層的最小值,通通相同。大可不必重複計算。
動態規劃化簡成貪心法。每一層的最小值,通通加總。
時間複雜度降為O(HW)。
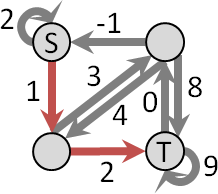
只能走往下、左、右(來自上、左、右)
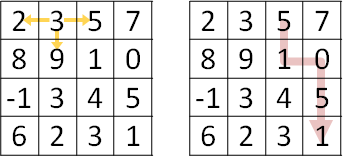
因為無法順利刪除下緣,所以只好深入分析問題。
走往左或右:一、可能左右單向行走,二、可能左右來回行走。
左右單向行走,得以順利刪除下緣:來源改成上一層任一格,再追加一段走過來的距離(區間和)。區間和等於累積和相減。累積和可以事先計算。
左右來回行走:甲、可能讓總和增加,乙、可能讓總和不變,丙、可能讓總和減少。
總和增加或不變,不適合來回行走,只適合單向行走。問題化作單向行走,問題已然解決。
總和減少,永遠走不完,問題的答案是無限小。檢查左右相鄰兩格數字總和是否為負值。
問題的分析流程如上所示。程式碼的寫作流程又是另外一回事。我不想囉嗦,大家自己琢磨吧。
時間複雜度O((HW)⋅W)。
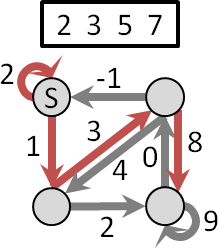
只能走往上、下、左、右(來自上、下、左、右)
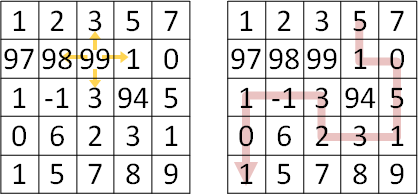
問題化作最短路徑問題。請見本站文件「shortest path」。
點有權重,邊無權重。點權重挪至入邊權重。
時間複雜度O((HW)²)。
雜談
題目稍微修改,解答大幅改變。沒有徵兆,毫無規律。
正是因為變化多端,沒辦法一語帶過,才需要寫下這份筆記。正是因為變化多端,沒辦法一勞永逸,才誕生工程師這樣的職位。
對於喜歡益智遊戲的人,變化是樂趣。對於處理實際問題的人,變化是困擾。人人都有不同想法。然而,天下本無事,庸人自擾之。即便不去學習這些變化,其實也沒什麼大不了。如果你認為這些變化無關緊要,那麼恭喜你,你很自由。