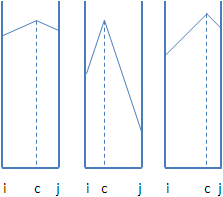
eccentricity
eccentricity(i) = max d(i, j)
j∊V
d(i, j) 為i點到j點的最短路徑
在一張無向圖上面,給定圖上一點,以最短路徑長度當作距離,找出離此點最遠的一點,這兩點之間的距離就叫做「偏心距」。
diameter / radius
diameter(G) = max eccentricity(i) = max d(i, j)
i∊V i,j∊V
radius(G) = min eccentricity(i)
i∊V
一張無向圖的「直徑」是圖上所有偏心距當中最大的一個,一張無向圖的「半徑」是圖上所有偏心距當中最小的一個。「直徑」也可以直接想做是,一張圖上長度最長的一條最短路徑之長度。
【註:有時候為了方便,直徑和半徑會定義成一段路徑,而不是一個數值。】
一張圖可能會有許多條直徑、許多條半徑。
直徑和半徑都是最短路徑。根據最短路徑的性質,直徑和半徑中間截取一段路徑,也是最短路徑。
要計算一張無向圖的直徑與半徑是很簡單的,首先算好所有兩點之間最短路徑,然後按照定義來算就可以了。
ICPC 3569
peripheral vertex
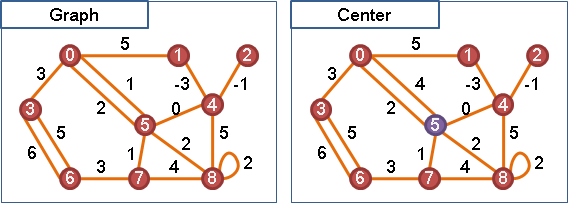
central vertex(center)
center(G) = arg min eccentricity(i)
i i∊V
= arg min max d(i, j)
i i∊V j∊V
d(i, j) 為i點到j點的最短路徑
一張無向圖的「中心」是圖上的一個點,離中心最偏遠的點,其距離會最小,也就是說「中心」的偏心距會等於半徑長度。一張無向圖可能會有很多個「中心」。
中心離圖上所有點越近越好,圖上所有點離中心越近越好。是以最偏遠的點的距離來衡量遠近,而非以各點的距離總和來衡量遠近。
要找到一張無向圖的中心是很簡單的,首先算好所有兩點之間最短路徑,然後按照定義來找就可以了。
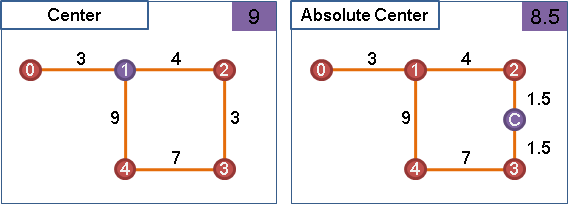
absolute center
absolute_center(G) = arg min eccentricity(i)
i i
= arg min max d(i, j)
i i j∊V
一張無向圖的「絕對中心」,與中心稍有不同。絕對中心不一定得是原圖上的點,它可以位於某條邊上的某處。一張無向圖可能會有很多個「絕對中心」。
演算法(Kariv–Hakimi algorithm)
此演算法跟一般圖論問題的解題手法完全不同。首先忘掉圖論,讓我們回到高中函數。
我們先假設絕對中心在邊ij上面。接著畫出一個函數圖形:X軸是絕對中心與i點的距離(想當然X軸範圍只有0到d(i,j)),Y軸是絕對中心與圖上x點的最短距離。先隨便選一個x點。
根據絕對中心在邊ij上面的各種位置,我們都可以算出絕對中心離x點的最短距離,進而描出一條函數線。這條函數線長得什麼樣子呢?以下分為三種情況討論:
甲、絕對中心在正權重的邊上游移:
觀察絕對中心到x點的最短距離變化。絕對中心挪往邊ij的中間,絕對中心到x點的最短距離就會慢慢增加;絕對中心挪往邊ij的兩端,絕對中心到x點的最短距離就會慢慢減少。左右的坡度是相同的,也可能只有左坡或者只有右坡。
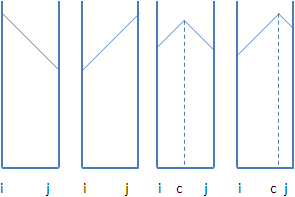
接著觀察絕對中心到圖上每一點的最短距離變化。我們可以把每一個點的函數線統統描在同一張函數圖形,每條線的坡度都是一樣的。
根據絕對中心的定義,絕對中心與最遠點的距離越小越好;對照到函數圖形,就是上方邊際線的Y軸座標越低越好。由此可知,上方邊際線的最凹處,就是絕對中心的偏心距大小;最凹處的投影位置,就是絕對中心的最佳位置。窮舉上方邊際線的所有凹處,找出最小的偏心距,就能找到絕對中心。
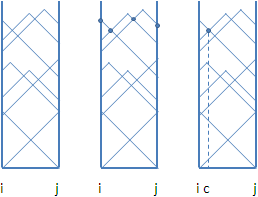
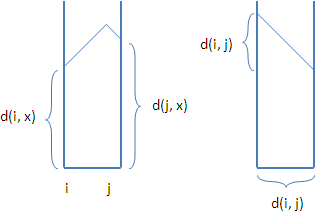
該如何找到上方邊際線的最凹處呢?這就要一點小技巧了。首先把每一條函數線的左端點按照高低排序,然後由最高的函數線開始,不斷與更低的函數線相交,交點即是上方邊際線的凹處。每次求得交點後,就留下原本較低的函數線,繼續與更低的函數線相交,最後就能得到所有凹處。Y軸座標最低的,就是最凹處了。
計算凹處的Y軸座標很簡單,只需要知道相交的兩條線在X軸的兩端分別有多高,就能推導出來了:
eccentricity(c)
= d(c, i) + d(i, x)
= d(c, j) + d(j, y)
= (d(i, j) + d(i, x) + d(j, y)) / 2
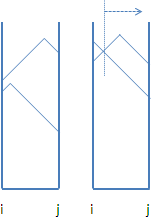
乙、絕對中心在負權重的邊上游移:
X軸左右兩端最高的函數線的交叉點,就是上方邊際線的最凹處。輕鬆寫意。
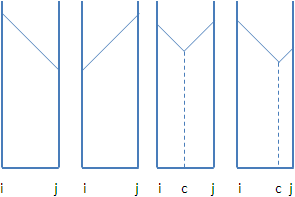

丙、絕對中心在零權重的邊上游移:
函數線都是水平線,最高的函數線到處都是最凹處。

最後,要找到一張無向圖的絕對中心,只需窮舉圖上所有邊,看看絕對中心在哪一條邊,再來依照方才的分析過程,取偏心距最小者即可。
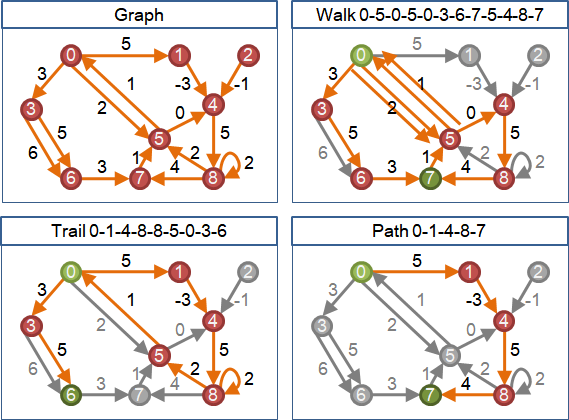
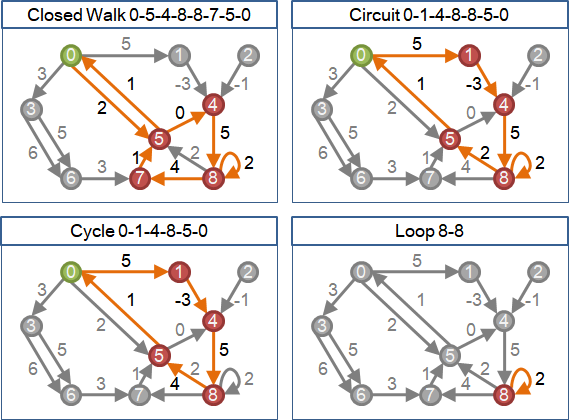
一、計算所有兩點之間最短路徑。
並且記錄起點到圖上各點的最短路徑長度順序。
二、窮舉圖上所有邊ij,找出絕對中心:
甲、正邊:i點、j點、上方邊際線所有凹處。O(V)。
乙、負邊:i側最高線與j側最高線的交叉點。O(1)。
丙、零邊:最高的水平線。O(1)。
時間複雜度
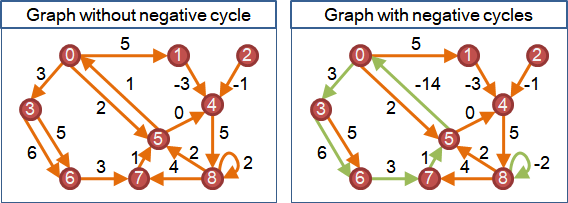
一、計算所有兩點之間最短路徑:有負邊,以minimum weight T-join求解,O(V⁴);無負邊,執行V次Dijkstra's algorithm,以Fibonacci heap實作,O(V(E + VlogV))。
二、尋找絕對中心:圖的資料結構為adjacency lists是O(VE)。
時間複雜度取決於計算最短路徑的時間。
實作
下面提供一個簡化過的實作,假設圖上的邊都是正權重。
這段程式碼沒有特別記錄絕對中心的位置,各位可以試著想一下怎麼記錄。
延伸閱讀:無權重圖的絕對中心
簡單來說,就是每一條邊的權重都是一。在這種情況下,要尋找絕對中心的位置就簡單多了,判斷方式會變得簡潔一點。
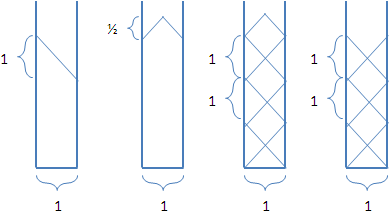
先判斷左右兩側最高點是否一樣高。
甲、如果不一樣高,上方邊際線就出來了,答案也就出來了。O(1)。
乙、如果一樣高,則需要判斷上方邊際線的凹凸。
檢查左右兩側最高點,是不是來自同一點的最短路徑長度,若是則為凸。O(V)。
計算兩點之間最短路徑,只需V次BFS,需時O(VE)。尋找絕對中心,仍需時O(VE)。總時間複雜度降為O(VE)。
UVa 10805
延伸閱讀:點有加權效果的絕對中心
absolute_center(G) = arg min max {d(i, j) ⋅ w(j)}
i i j∊V
令圖上的點與邊都擁有正權重,距離重新定義為最短路徑乘上端點的權重。在此狀況下,尋找絕對中心,變得要排序,需時O(VElogV)。各位可以想一想怎麼做。