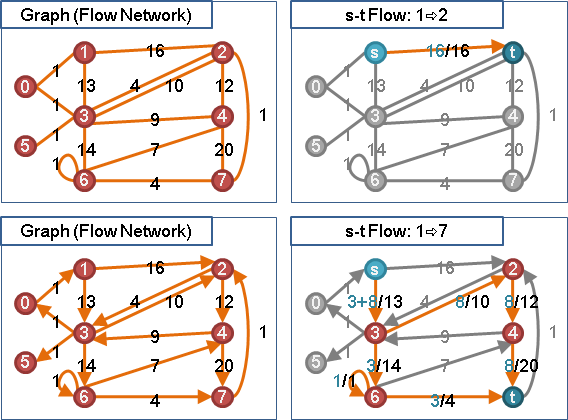
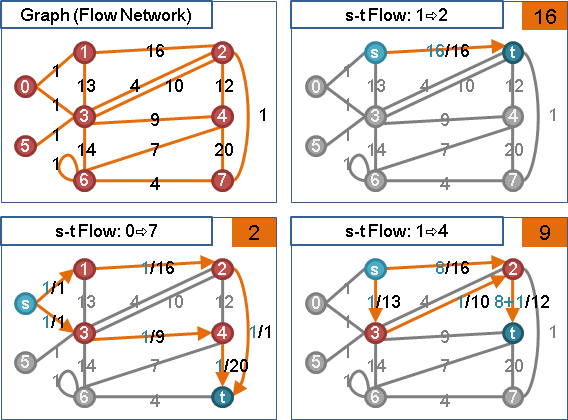
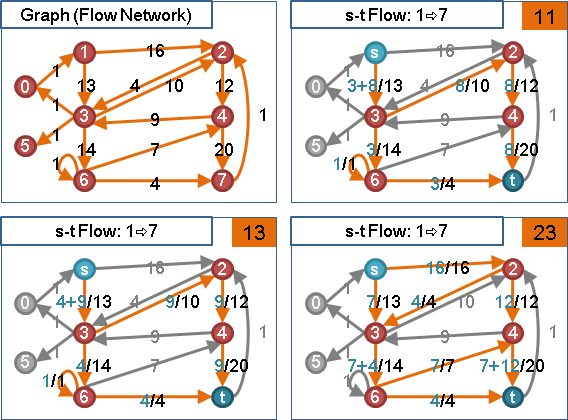
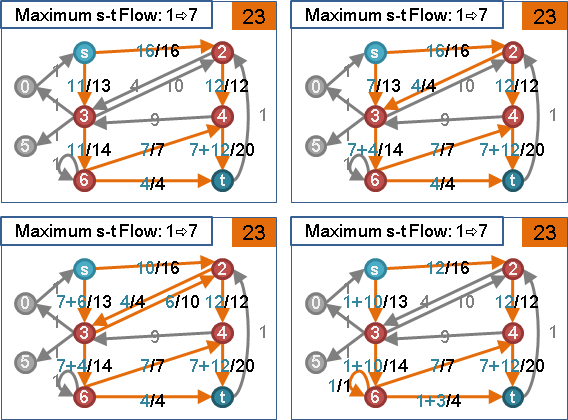
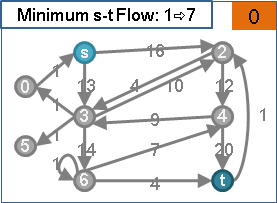
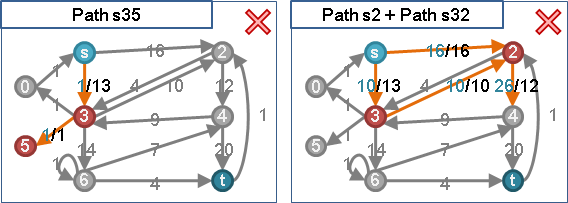
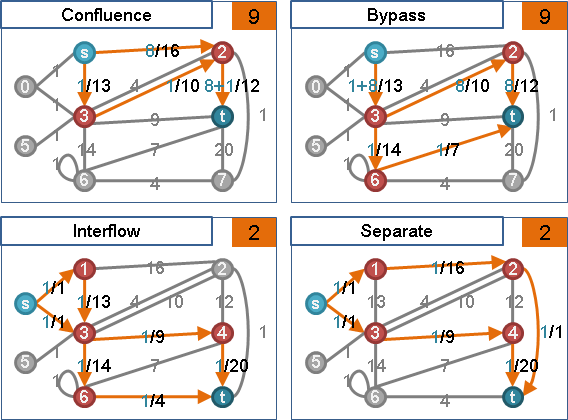
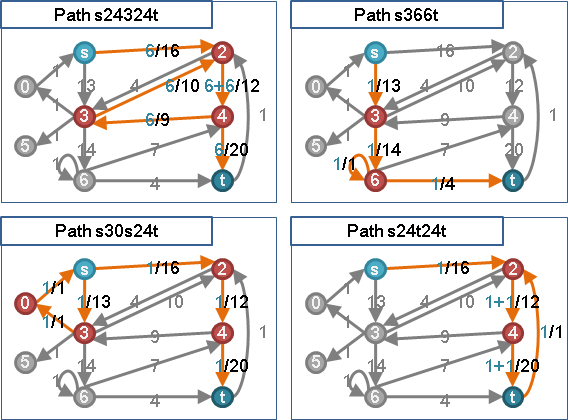
🕛preflow
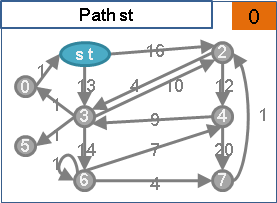
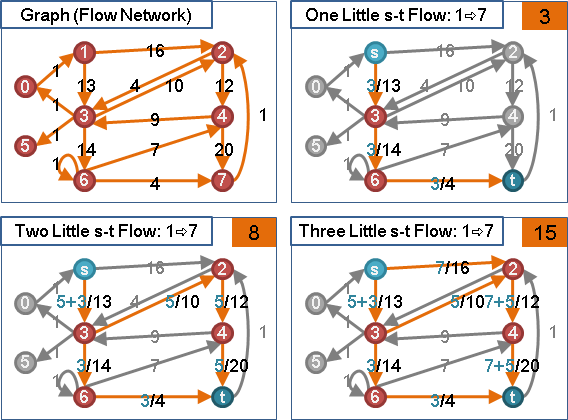
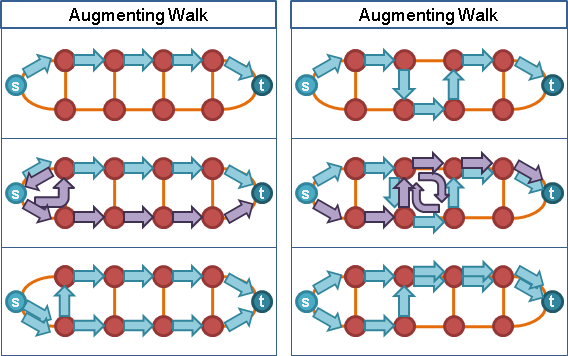
想像一下:模仿針筒注射、發射水槍。源點放入足夠水量,然後用力推擠源點,讓源點的水一股作氣鑽過整張圖,從匯點噴出水流。
受限於管線容量瓶頸,水流流量是有上限的。水鑽過整張圖的路線,就是一個最大流。匯點噴出的水流流量,就是最大流的流量。
然而電腦程式無法直接實現「一股作氣鑽過整張圖」,電腦程式只能一步一步計算。我們只好「一點接著一點慢慢送水」:首先源點送水到其它中繼點,然後中繼點送水到其他中繼點,直到匯點。
🕐excess
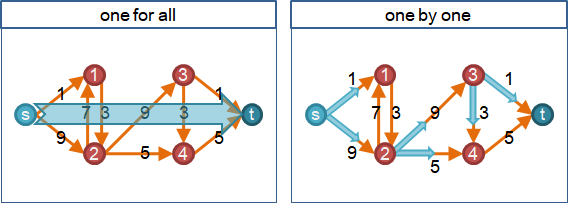
為了實現「一點接著一點慢慢送水」的想法,讓圖上每個點都可以暫時儲存水,稱作「積水點」。儲存水量,稱作「積水量」。一個點收到水之後,可以暫時儲存,可以隨時送水到其他點。
建立「積水點」和「積水量」之後,水一直存在、不會消失。即便送水送錯地方,也可以往回送水,調校水流流向。
以「積水點」和「積水量」設計最大流演算法:
一、源點的積水量,設定成無限大。
二、源點送水到各點,慢慢送水到匯點,送水順序隨意。
三、遇到管線容量瓶頸,多餘的水量將停留在點上。
四、最後能夠送到匯點的水量,就是最大流的流量。
🕑residual capacity
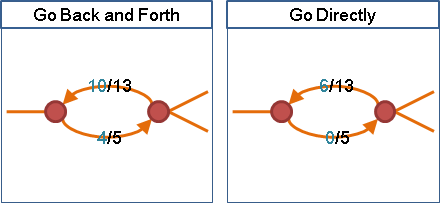
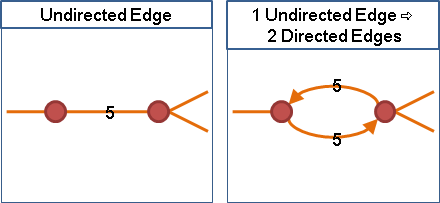
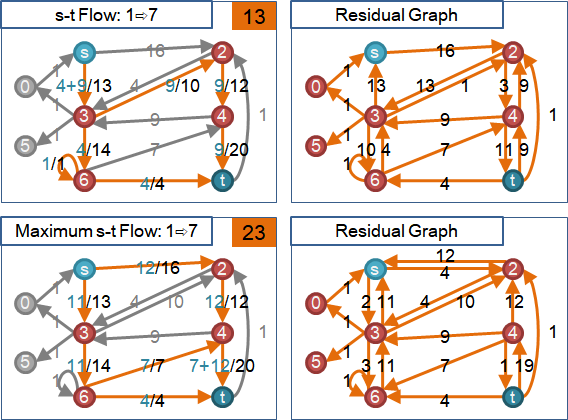
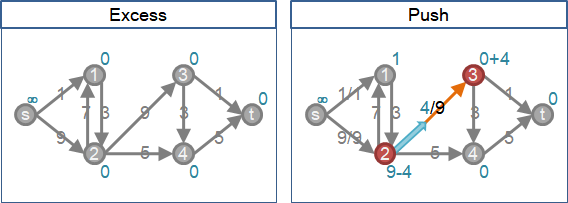
圖上每條邊都擁有流量,流量大於等於零、小於等於容量。
正向邊的流量與容量差距、反向邊的流量(溯洄沖減),兩者相加,得到「剩餘容量」。
以「剩餘容量」設計最大流演算法:
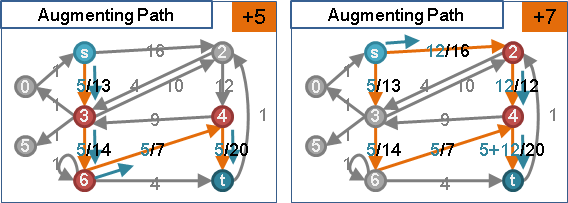
一、根據剩餘容量,盡量灌滿流量。模仿針筒注射、發射水槍。
二、利用剩餘容量,調校水流流向。送水送錯地方,可以往回送水。
🕒height
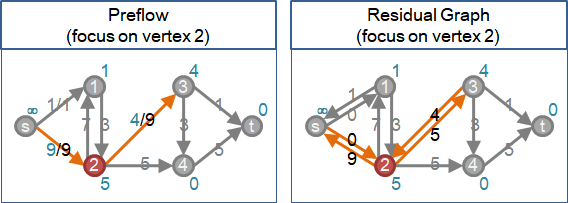
為了實現「一點接著一點慢慢送水」的想法,必須確保流向正確,避免來回送水,避免繞圈送水。
引入「水往低處流」的想法。讓圖上每個點都有「高度」,由高往低送水。
以「水往低處流」設計最大流演算法:
一、由源點漫溢:源點是最高點。
二、朝匯點聚集:匯點是最低點。
三、源點往匯點:其他點比源點低、比匯點高。
四、避免繞圈送水:不能送水到一樣高的鄰點。只能送水到更低的鄰點。
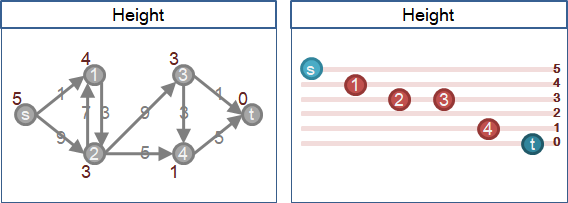
再引入「一點接著一點慢慢送水」的想法。只有「高度」剛好低一層的鄰點,才可以送水。
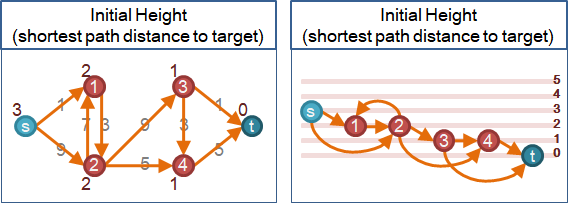
以「一點接著一點慢慢送水」設計最大流演算法:
一、高度可以安排為:以匯點為終點的最短路徑長度,作為高度。
二、送水規則可以制定為:一個點只能送水到「剛好低一層」的鄰點。
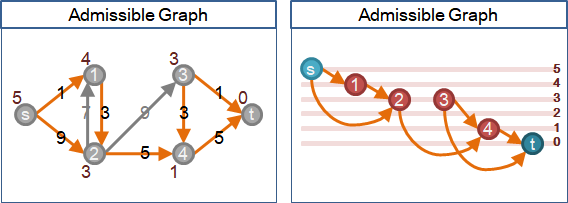
🕓admissible edge
以剩餘容量、高度,制定水流的遵行方向。
一條邊,剩餘容量大於零、高度減少一,形成「容許邊」。
出現新麻煩:無法調校水流流向。
🕔relabel
為了實現「調校水流流向」的想法,讓圖上每個點都可以「抬高」。
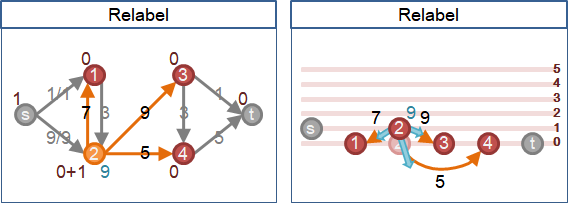
甚至最初將高度通通設為零,放任圖上各點自由抬高。
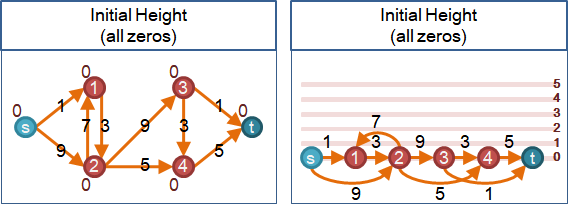
🕕push
一個積水點想要「送水」到鄰點,那就抬高積水點,比鄰點高一層。如果流量已滿,那就抬更高。
一個積水點想要「送水」到鄰點,需要注意三件事:一、點的積水量。盡量排空水量。二、鄰邊的剩餘容量。盡量灌滿流量。三、鄰點的高度。高度低一層。
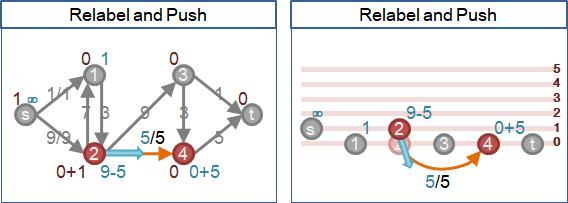
🕖retreat
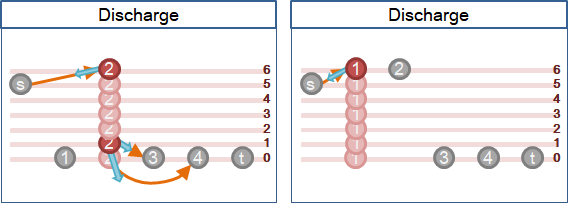
積水點下游遭遇瓶頸(甚至沒有管線),導致積水點水洩不通、積水難消,那就繼續抬高、往回送水,稱作「撤退」。
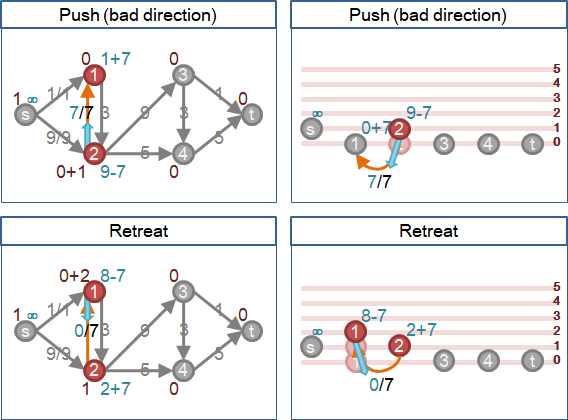
🕗discharge
為了實現「一點接著一點慢慢送水」的想法,讓圖上每個點都可以「排水」。不斷抬高,不斷送水,把水排乾。
排水可以避免一鼓作氣送水到最低點,結果發現送錯方向,又從最低點一路撤退回到原點。排水可以大幅減少送水次數。
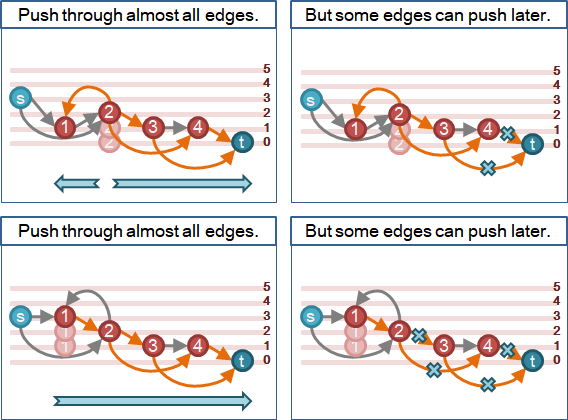
一個積水點有許多鄰點。首先抬高積水點,稍高於最低鄰點,送水到最低鄰點,盡量灌滿流量。如果仍有積水,再度抬高積水點,稍高於次低鄰點,送水到次低鄰點,盡量灌滿流量。以此類推,直到積水用罄。
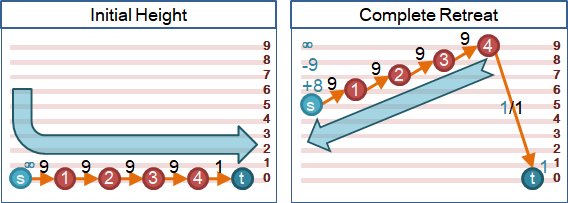
🕘complete retreat
當水量過剩,許多水無處可去。繼續抬高每個點,直到比源點高,讓多餘的水回歸源點──剛好作為演算法的閉幕。最後圖上的水流流動情形就是最大流。
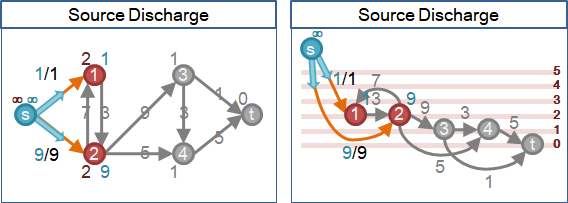
🕙source discharge
抬高過程當中,源點與鄰點不斷來回送水,浪費時間。預先讓源點強制送水到所有鄰點,並且大幅抬高源點,節省時間。
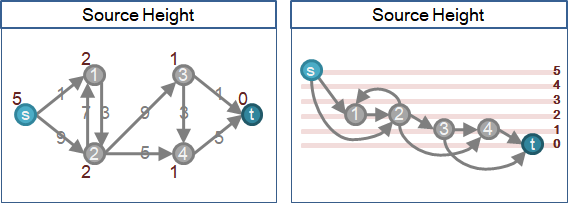
🕚source height
擴充路徑長度最多V-1。源點高度與匯點高度最多相差V-1。如果相差超過V-1,源點絕對無法送水到匯點。
預先讓源點高度固定為V-1,匯點高度固定為0,其他點自由抬高。V是圖上的點數。
小結
想讓水「一股作氣鑽過整張圖」,電腦卻只能「一點接著一點慢慢送水」。只好創立「積水點」,引入「水往低處流」的想法,以匯點為終點的最短路徑長度作為「高度值」,迫使水流向匯點。創立「抬高」,以便調校水流流向。創立「排水」,避免一鼓作氣送水到最低點。多餘的水,無法到達匯點,藉由抬高,順利回歸源點。
方才設計的最大流演算法:
一、由源點漫溢:源點高度固定為V-1。
二、朝匯點聚集:匯點高度固定為0。
三、前往匯點:抬高一個點,比匯點高。
四、回歸源點:抬高一個點,比源點高。
五、避免繞圈送水:不能送水到一樣高的鄰點。只能送水到剛好低一層的鄰點。
六、調校水流流向:抬高一個點,比鄰點高一層,以便送水到剛好低一層的鄰點。
接下來開始詳細列出演算法內容。
push
積水點送水到鄰點。
一、積水點不是源點和匯點。(源點已排水,匯點只收水。)
二、積水點仍有水。
三、積水點到鄰點仍有剩餘容量。
四、積水點到鄰點剛好下降一層。
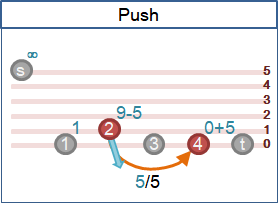
relabel
積水點抬高:直到可以送水至鄰點。
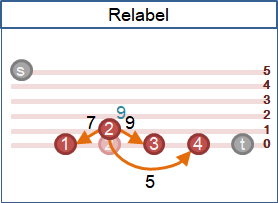
discharge
積水點排水:不斷push和relabel,直到沒水。
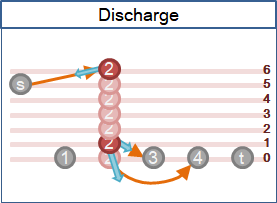
height
以匯點為終點的最短路徑長度,作為高度。
可以省略不做。一律設為0,不影響結果。然而會額外抬高許多次,浪費時間。
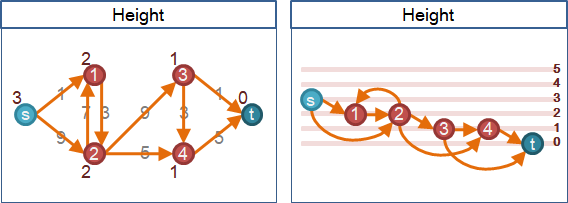
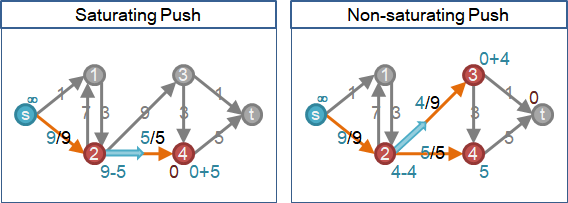
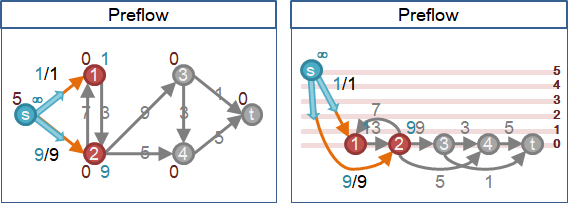
preflow【原始論文將source discharge叫做preflow】
一、源點高度固定為V-1,匯點高度固定為0。
二、源點積水量無限大。
三、源點強制送水到所有鄰點,無視高度。
可以省略不做。限制源點高度低於V,不影響結果。然而會額外抬高許多次,浪費時間。
演算法:一直找任意積水點送水或抬高
(push–relabel algorithm)
1. height。(可省略)
2. preflow。(可省略,但是要限制源點高度低於V。)
3. 不斷push或relabel,次序隨意,直到無法進行為止。
preflow algorithm改良版。隨時調整高度值、容許圖。容許圖從靜態變成動態(嚴格來說是自適應adaptive)。
僅以兩種「點對鄰點」的動作push、relabel,求得最大流。十分精采!
時間複雜度
我們針對push、relabel的次數下手。
relabel抬高:源點高度設為V-1,匯點高度設為0。最差情況下,除源點匯點,最高點升到了2V-3、最低點升到了V。
一個點O(V)次,所有點O(V²)次。一次O(deg(vᵢ)),總共O(VE)。
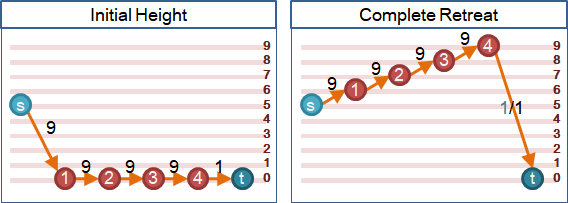
saturating push灌到滿:一條邊,兩個端點逐漸升高,高度範圍為0到2V-3,高度相差一才能送水,一種高度最多送水一次。
一條邊O(V)次,所有邊O(VE)次。一次O(1),總共O(VE)。
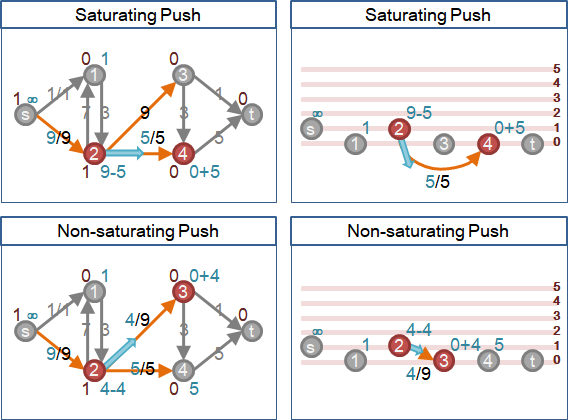
non-saturating push灌不滿:同上,但是端點可從鄰點補充水量,最多補充V-2次。一種高度最多送水V-1次。
一條邊O(V²)次,所有邊O(V²E)次。一次O(1),總共O(V²E)。
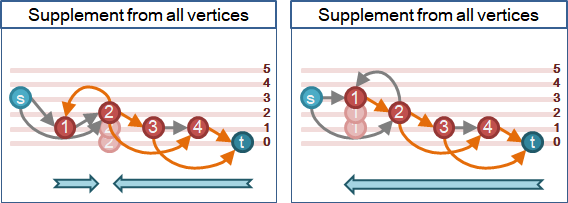
時間複雜度O(V²E),受限於non-saturating push。
演算法:積水點以任意順序排水
1. height。(可省略)
2. preflow。(可省略,但是要限制源點高度低於V。)
3. 不斷discharge,次序隨意,直到無法進行為止。
改成discharge,效率沒有顯著提升。
演算法:積水點以FIFO順序排水
(FIFO push–relabel algorithm)
1. 建立一個queue,塞入積水點(不包括源點匯點),積水點不重複。
2. queue不斷彈出點,進行discharge,直到queue無點。
當discharge產生新的積水點,而且queue沒有這個積水點,就塞入queue。
relabel抬高:時間複雜度同前。
saturating push灌到滿:時間複雜度同前。
non-saturating push灌不滿:援引preflow algorithm的分析技巧。所有邊O(V³)次。總共O(V³)。
時間複雜度降為O(V³)。
演算法:一直找最高的積水點排水
(highest-label push–relabel algorithm)
宛如一口氣尋找所有擴充路徑。
時間複雜度降為O(V²sqrtE)。
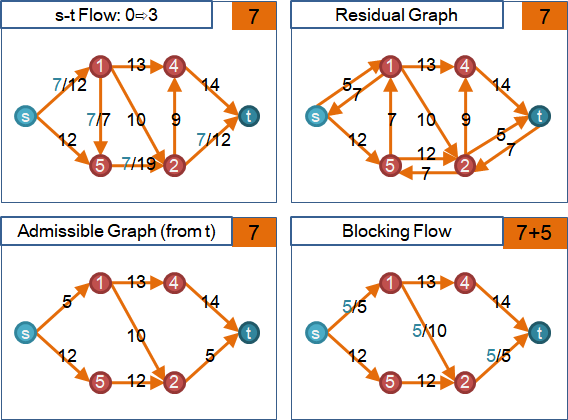
加速技巧:blocking flow
容許圖,源點到匯點連通,才能送水。
容許圖,鄰點高度差一。想要保持連通,每種高度缺一不可。
圖上各點不斷抬高。任何一種高度,一旦出現又消失,表示更高點到更低點不連通,形成阻塞流。更高點無法送水到更低點。更高點即將全面撤退。更高點大可不必再排水、抬高、送水,以節省時間。
建立高度直方圖,隨時判斷連通。一旦不連通,拋棄更高點,使之無作為。中文網路稱作「gap优化」。
注意到,這個技巧只能求得最大流流量,無法求得最大流。