cut

「割」有兩種定義方式：

一、「割」是點集合：圖上所有點分成第一群和第二群。

二、「割」是邊集合：第一群點連向第二群點的邊。

「割」還有另一種觀點：

一、「割」是點集合：從圖上挑出一群點。

二、「割」是邊集合：一群點連向其他點的邊。

點分成兩群，一種分法就是一個cut。所有點可以集中在同一群，此時另一群就是空的。

V個點的有向圖，一共有2ⱽ種cut。V個點的無向圖，第一群和第二群的順序沒有差別，一共有2ⱽ/2種cut。

一個cut的權重，是所有邊的權重總和。

minimum cut

「最小割」。一張圖權重最小的割，可能有許多個。

求最小割是NP-hard問題。當圖上沒有負邊，才是P問題。

maximum cut

最大割和小割很類似。最大割問題當中，每一條邊的權重添上負號，就變成最小割問題。反過來也是。

求最大割是NP-hard問題。當圖上沒有正邊，才是P問題。

一群點收縮為一個點

同群的點收縮成單獨的點，cut的權重依舊相同。

多重的邊變成單獨的邊

多重的邊合併成單獨的邊，權重加總，cut的權重依舊相同。

s-t cut

「源匯割」。s點位在第一群、t點位在第二群。

s點、t點所屬的點集合，以下稱作s側、t側。

minimum s-t cut

「最小源匯割」。指定兩個點（源點和匯點），這兩個點在不同側的最小割，可能有許多個。

數學性質：叛離

以下介紹幾個minimum s-t cut的數學性質。針對無向圖、無負邊。性質名稱是我隨興取的。歡迎各位讀者提供建議。

s側或t側分離出一群點（s點與t點不移動），得到不等式：

一側分離出一群點到另一側（s點與t點不移動），權重變大，或者權重不變（遇到另一個最小st割）。

數學性質：基準

x點在s側，y點在t側，最小xy割的權重小於等於最小st割的權重。

最小xy割的背後有著最小st割撐腰，青出於藍更勝於藍。

數學性質：共側

圖上任取三點ijk，求出最小ij割、最小jk割、最小ki割。

權重較小的那兩個割，權重相等（甚至是同一個割）。

一、不失一般性，權重最小的那一個割，暫定是最小ij割。
二、要嘛k點在i側，要嘛k點在j側。
　甲、暫定k點在j側。
　　　由基準性質可知：最小kj割的權重小於等於最小ij割的權重。
　　　又因為最小ij割已經是權重最小的，
　　　所以，最小kj割的權重被迫等於最小ij割的權重。
　乙、暫定k點在j側。
　　　同理，最小ki割的權重被迫等於最小ij割的權重。

數學性質：minimality

基準性質、共側性質，改寫成min函數。但是性質變弱失真。

圖上任意三點ijk
mincut(i,k) ≥ min(mincut(i,j), mincut(j,k))
推廣至任意序列
mincut(a,z) ≥ min(mincut(a,b), mincut(b,c), ..., mincut(y,z))

用途

無向圖或有向圖，指定源點與匯點，求出其中一個最小源匯割。

限制：無負邊。

max-flow min-cut theorem

有向圖當中，根據「最大流最小割定理」，「有向圖的最大源匯流」同時形成了「有向圖的最小源匯割」。

無向圖當中，預先把一條無向邊換成兩條有向邊，「有向圖的最大源匯流」同時形成了「無向圖的最小源匯割」。

最大源匯流，部分管線滿溢，達到容量上限，形成瓶頸，其中包含了最小源匯割。

演算法

一個最大源匯流，通常可以找到多個最小源匯割。

由源點開始遍歷，只通過管線尚未滿溢的邊，得以觸及的點集合（瓶頸之前）、無法觸及的點集合（瓶頸之後），就是其中一個最小源匯割，而且源點側的點數最少。

由匯點開始反向遍歷，亦有類似結果。

typedef int Graph[9][9]; // adjacency matrix Graph C, F, R; // 容量、流量、剩餘容量 bool visit[9]; void DFS(int i) { visit[i] = true; for (int j=0; j<9; ++j) if (!visit[j] && F[i][j] < C[i][j]) DFS(j); } void minimum_cut(int s, int t) { // 求一個最大源匯流，源點為s點，匯點為t點。 maximum_flow(s, t); // 從源點開始遍歷，找出流量瓶頸。 memset(visit, false, sizeof(visit)); DFS(s); // 找出其中一個最小源匯割，源點側的點數最少。 for (int i=0; i<9; ++i) // 窮舉源點側的點 if (visit[i]) for (int j=0; j<9; ++j) // 窮舉匯點側的點 if (!visit[j]) if (C[i][j] > 0) // 要確定有邊 cout << "割上的邊有" << "由" << i << "到" << j; }

UVa 10480 ICPC 5099

minimum cut

圖上每種點對作為源點和匯點，分別尋找源匯最小割。其中最小者就是最小割。

用途

無向圖或有向圖，指定源點，窮舉匯點，求出權重最小的最小源匯割。通常有許多個，找到其中一個。

限制：無負邊。

想法：窮舉法

固定源點，窮舉匯點，分別計算V-1次最小源匯割，其中最小者就是正解。

想法：遞歸法

圖上隨意取一條邊，要嘛在割上，要嘛不在割上。

圖上隨意取兩個點，要嘛在割異側，要嘛在割同側。

考慮正解。圖上隨意取兩個點，s點與t點。

一、s和t在正解的異側：最小st割就是正解。

二、s和t在正解的同側：收縮st兩點，不影響正解。

收縮之後，圖上減少了一點，得以實施遞歸法！

匯點收縮至源點，任選一個新匯點，總共計算V-1次最小源匯割，其中最小者就是正解。

圖上逐次減少了一點，計算速度變快了一點。

想法：多個源點

「匯點收縮至源點」重新解讀為「新增源點」。

舊匯點變成新源點，任選一個新匯點，總共計算V-1次最小多源單匯割，其中最小者就是正解。

演算法

push–relabel algorithm輕輕鬆鬆將舊匯點變成新源點。

一、指定源點。
　　源點以外隨意取一個點，作為匯點。
二、實施push–relabel algorithm，尋找最大多源單匯流。
　甲、沿用上次計算結果。
　乙、舊匯點變成新源點。
　　　新源點實施preflow：高度固定為V-1、積水量無限大、強制送水到所有鄰點。
　丙、任選一個最低點變成新匯點。
　　　高度固定為當前高度。
　丁、繼續實施push和relabel，找到新的最大多源單匯流。
　戊、由源點開始遍歷，找到新的最小多源單匯割。
三、重複上述步驟V-1次，得到V-1個最小多源單匯割，其中最小者就是正解。

時間複雜度

因為圖上各點高度上限仍然相同，所以時間複雜度仍然相同。

時間複雜度等同一次push–relabel algorithm的時間O(V²E)。

改用FIFO push–relabel algorithm降為O(V³)。改用highest-label push–relabel algorithm降為O(V²sqrtE)。

加速技巧：blocking flow

圖上各點不斷抬高。任何一種高度，一旦出現又消失，表示更高點到更低點不連通，形成阻塞流。更高點作為源點側，更低點作為匯點側，形成源匯割。

每當任何一種高度出現又消失，更高點納入源點側，其餘點作為匯點側，最後得到最小源匯割。

一旦找到最大源匯流，同時得到最小源匯割。不必另行遍歷。

minimum cut

圖上各點分別作為源點，分別實施Hao–Orlin algorithm。其中最小者就是最小割。

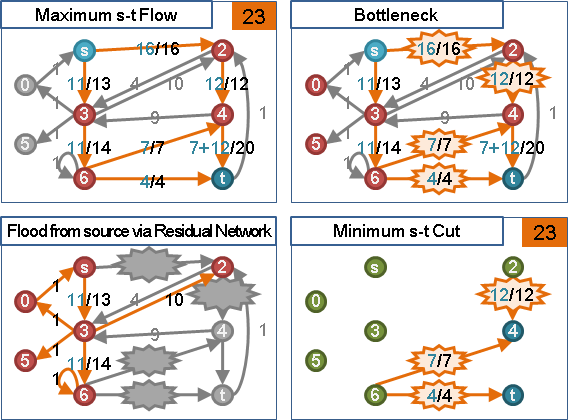
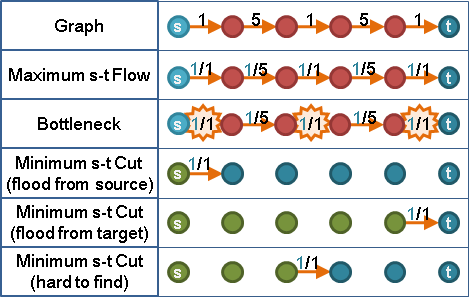
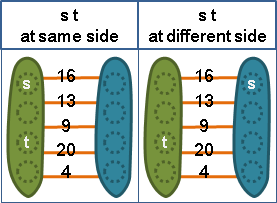
用途

無向圖，無法指定源點與匯點，求出任意一個最小源匯割。

限制：無負邊。

maximum adjacency search

「maximum cardinality search」引入權重。每回合找到一個點，連往已拜訪點的權重總和最多。若不只一點，則任選一點。

時間複雜度O(V²)。運用binary heap壓至O(V+ElogV)。運用Fibonacci heap壓至O(E+VlogV)。

int adj[9][9]; // adjacency matrix int w[9]; // 記錄各點到目前的A集合的距離 bool visit[9]; // 記錄各點是不是已經加入A集合 void maximum_adjacency_search() { for (int i=0; i<9; ++i) visit[i] = false; for (int i=0; i<9; ++i) w[i] = 0; for (int i=0; i<9; ++i) { // 找出一個尚未加入A當中、且w(A, x)最大的x點。 int x = 0, max = -1e9; for (int j=0; j<9; ++j) if (!visit[j] && w[j] > max) max = w[j], x = j; visit[x] = true; // 加入x點到A集合 cout << "遍歷到第" << x << "點"; // 加入x點到A集合後，更新w(A, x)的值。 for (int j=0; j<9; ++j) if (!visit[j]) w[j] += adj[x][j]; } }

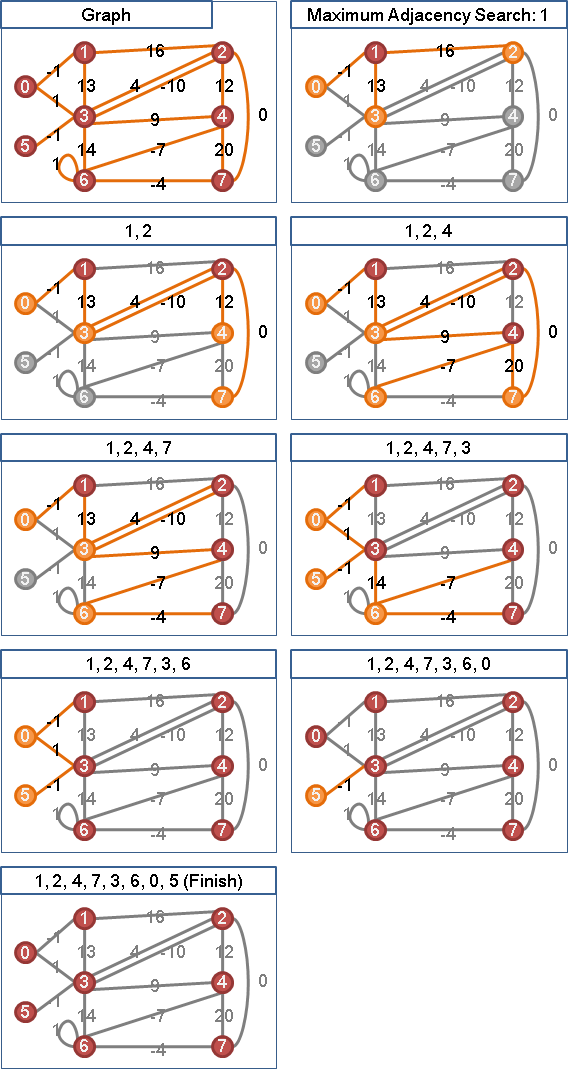
當圖上無負邊，
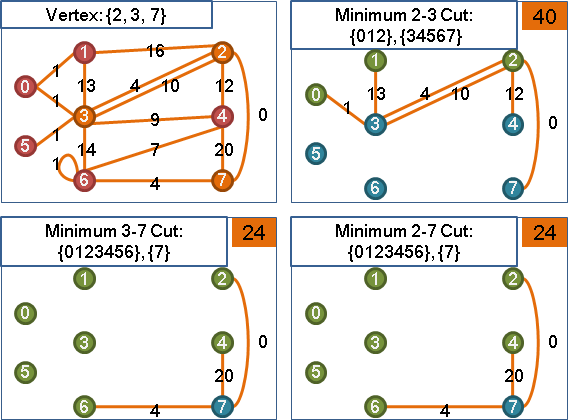
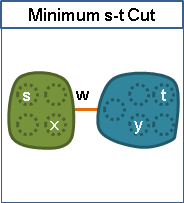
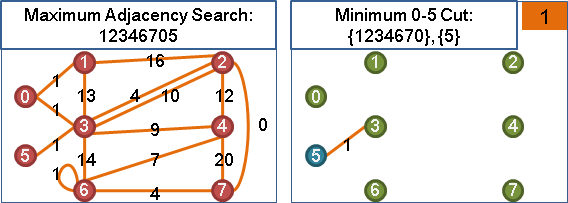
maximum adjacency search最後兩點形成minimum s-t cut

令maximum adjacency search的遍歷順序是v₁…vₙ，最後兩點是vₙ₋₁與vₙ。

當圖上無負邊，{v₁…vₙ₋₁}與{vₙ}是一個最小vₙ₋₁vₙ割。

一、欲證cut(v₁⋯vₙ₋₁, vₙ)是最小vₙ₋₁vₙ割。
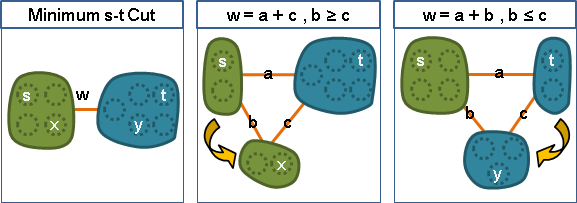
二、觀察vₙ₋₂與vₙ₋₁與vₙ這三點，根據共側性質，
　　最小vₙ₋₂vₙ₋₁割、最小vₙ₋₂vₙ割、最小vₙ₋₁vₙ割，
　　其中權重比較小的那兩個割，權重相等。
三、嘗試找到最小vₙ₋₂vₙ₋₁割、最小vₙ₋₂vₙ割，
　　並且證明cut(v₁⋯vₙ₋₁, vₙ)的權重同時小於等於這兩個割，
　　那麼根據共側性質，cut(v₁⋯vₙ₋₁, vₙ)就一定是最小vₙ₋₁vₙ割。
四、以下用數學歸納法證明，但是以反方向講解。

basis step:
圖上只有兩點一邊時，顯然是一個最小st割。

inductive step:
一、從圖上移除邊vₙ₋₁vₙ，
　　不影響vₙ₋₁vₙ割的位置，刪除也無妨。
二、最小vₙ₋₂vₙ₋₁割的部分：
　甲、從圖上移除vₙ（以及連著的邊）。
　　　重新實施maximum adjacency search，順序仍舊相同，vₙ₋₂與vₙ₋₁成為最後兩點。
　　　遞迴求解，證得cut(v₁⋯vₙ₋₂, vₙ₋₁)是一個最小vₙ₋₂vₙ₋₁割。
　乙、因為vₙ₋₁與vₙ兩點之間沒有邊，
　　　把vₙ（以及連著的邊）加回到cut(v₁⋯vₙ₋₂, vₙ₋₁)的vₙ₋₂側，
　　　得到cut(v₁⋯vₙ₋₂ + vₙ, vₙ₋₁)是原圖的一個最小vₙ₋₂vₙ₋₁割。
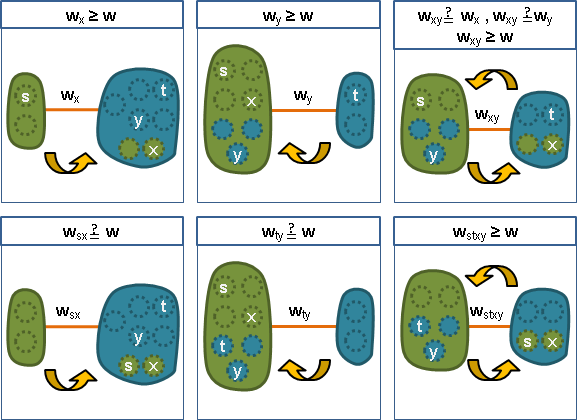
　丙、由maximum adjacency search倒數第二步的選擇，可知
　　　cut(v₁⋯vₙ₋₂, vₙ₋₁) ≥ cut(v₁⋯vₙ₋₂, vₙ)
　　　又因為vₙ₋₁與vₙ兩點之間沒有邊，
　　　cut(v₁⋯vₙ₋₂ + vₙ, vₙ₋₁) ≥ cut(v₁⋯vₙ₋₂ + vₙ₋₁, vₙ)
　　　顯然地，
　　　cut(v₁⋯vₙ₋₂ + vₙ, vₙ₋₁) ≥ cut(v₁⋯vₙ₋₁, vₙ)
　　　也就是說，cut(v₁⋯vₙ₋₁, vₙ)的權重小於等於最小vₙ₋₂vₙ₋₁割。
三、最小vₙ₋₂vₙ割的部分：
　甲、從圖上移除vₙ₋₁（以及連著的邊）。
　　　重新實施maximum adjacency search，順序仍舊相同，vₙ₋₂與vₙ成為最後兩點。
　　　遞迴求解，證得cut(v₁⋯vₙ₋₂, vₙ)是一個最小vₙ₋₂vₙ割。
　乙、因為vₙ₋₁與vₙ兩點之間沒有邊，
　　　把vₙ₋₁（以及連著的邊）加回到cut(v₁⋯vₙ₋₂, vₙ)的vₙ₋₂側，
　　　得到cut(v₁⋯vₙ₋₂ + vₙ₋₁, vₙ)是原圖的一個最小vₙ₋₂vₙ割。
　丙、顯然地，
　　　cut(v₁⋯vₙ₋₂ + vₙ₋₁, vₙ) = cut(v₁⋯vₙ₋₁, vₙ)
　　　也就是說，cut(v₁⋯vₙ₋₁, vₙ)的權重小於等於最小vₙ₋₂vₙ割。
四、由二丙、三丙，得證。

minimum cut

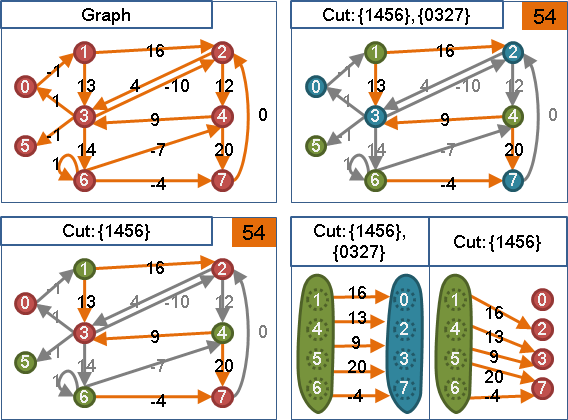
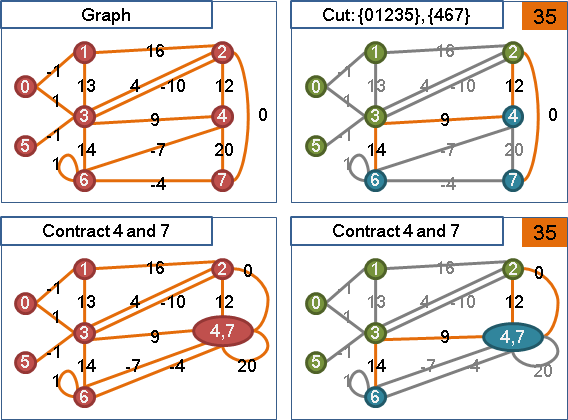
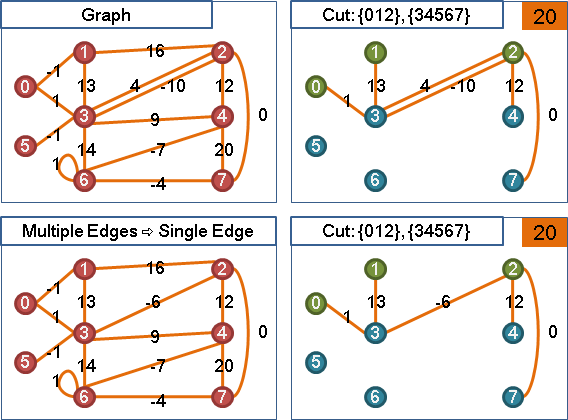
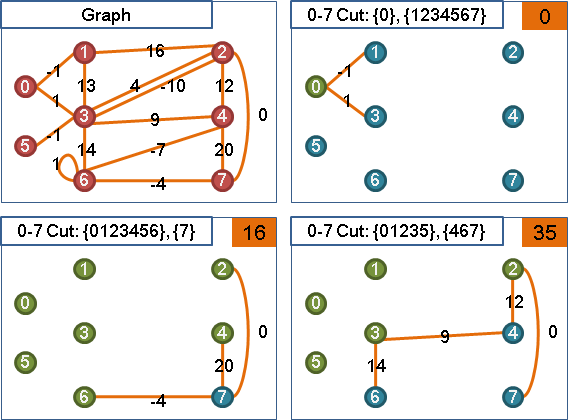
收縮源點與匯點，重做maximum adjacency search，總共計算V-1次源匯最小割，其中最小者就是最小割。

這個演算法後來被Stoer和Wagner重新提起。也許是因為他們倆的論文內容更加簡單明瞭，於是演算法名稱就變成他們倆了。

用途

無向圖，求出其中一個最小割。

限制：無負邊。

想法

圖上隨意取一條邊，要嘛在割上，要嘛不在割上。

圖上隨意取兩個點，要嘛在割異側，要嘛在割同側。

藉由此觀察，得以實施divide-and-conquer method。任取st兩點，分別計算這兩種情況下的最小割：

一、假設st在最小割異側：最小割根本就是最小st割。

二、假設st在最小割同側：原圖收縮st兩點，不影響最小割位置。圖上少了一點，就能遞迴求解，得到最小割。

因為沒有限制st是哪兩點，所以可以用maximum adjacency search快速求得st異側的那個最小st割。

注意到，這兩種情況其中一種肯定是假設錯誤的（當最小割只有唯一一個）。假設矛盾的情況下，根據邏輯，計算結果有可能是正版最小割，也有可能是權重亂七八糟的山寨最小割。

因此，還必須證明，假設矛盾的情況下，不管計算結果為何，那些山寨最小割一定比正版最小割來得差：

一、最小割根本不是st同側：正版最小割包含邊st，顯然邊st權重比較小。因為權重較小的邊被收縮了，所以遞迴求得的割通通大於正版最小割（或等於，當有多個最小割）。

二、最小割根本不是st異側：正版最小割不用邊st，顯然邊st權重比較大。因為最小st割一定用到邊st，所以最小st割大於正版最小割（或等於，當有多個最小割）。

如此一來就能保證，兩種情況下分別求得的最小割，權重較小的那一個，一定是正版最小割。

這比一般的divide-and-conquer method還要複雜一點。

演算法

一、用maximum adjacency search隨便求一個minimum s-t cut。
二、收縮s點與t點，重複步驟一，直到圖上只剩一點。
三、這V-1個minimum s-t cut當中，權重最小者，即是minimum cut。

時間複雜度

下列兩項總和，主要取決於第一項：

一、V-1次maximum adjacency search。

二、收縮點，收縮V-1次。圖的資料結構為adjacency matrix是O(V²)，圖的資料結構為adjacency lists是O(V)。

找出一個最小割

實作時要小心圖不連通的情況，圖不連通的地方就是最小割，權重為零。

int adj[9][9]; // adjacency matrix int contract[9]; // 記錄各點收縮之後的新編號 // 可以視作disjoint sets void stoer_wagner() { for (int i=0; i<9; ++i) contract[i] = i; int cost = 0; // minimum cut的權重 int cut[9], n = 0; // minimum cut的t側、t側點數 for (int k=0; k<9-1; ++k) { // 隨便找一個minimum s-t cut int s, t, c; maximum_adjacency_search(s, t, c, adj, contract); /* 如果s點與t點在minimum cut的異側 */ // 記錄權重比較小的minimum s-t cut if (c < cost) { cost = c; n = 0; for (int i=0; i<9; ++i) if (contract[i] == t) cut[n++] = i; assert(n == k+1); } /* 如果s點與t點在minimum cut的同側 */ // t點併至s點 for (int i=0; i<9; ++i) if (contract[i] == t) contract[i] = s; // t點連著的邊併至s點 for (int i=0; i<9; ++i) // 只找尚存的點！ if (i != s && contract[i] == i) { adj[i][s] += adj[i][t]; adj[s][i] += adj[t][i]; } } }

UVa 10989

用途

無向圖，求出其中一個最小割。

Monte Carlo algorithm，不保證答案百分之百正確。

演算法

圖上隨意取一條邊，要嘛在最小割上，要嘛不在最小割上。

圖上隨意取兩個點，要嘛在最小割異側，要嘛在最小割同側。

通通當作不在最小割上、都在同側，事情不就簡單多了？

重複下述步驟V-1次，直到圖上剩下兩個點，得到一個割，推定為最小割：
甲、隨機取圖上一條邊。
乙、推定這條邊不在最小割上，
　　也就是推定這條邊的兩個端點在最小割同側。
　　收縮這條邊的兩個端點，不影響最小割權重。

Kruskal's algorithm也是每次選擇一條邊、連結兩端點。兩者的差異，在於Karger's algorithm是隨機選擇一條邊，而Kruskal's algorithm是選擇權重最小的邊。

時間複雜度不知如何計算，可能很接近O(V+E)吧。

正確率

既然是隨機化演算法，就得計算一下正確率了！

令一張圖的最小割有c條邊。

補充零邊，令圖上每一個點連著c條邊。如此一來，圖上每一個割都有c條邊、每一個割都可能成為最小割，利於分析。

現在圖上總共c⋅V/2條邊。V是點數。

隨機從圖上選擇一條邊，這條邊在最小割上的機率是c / (c⋅V/2) = 2/V，不在最小割上的機率是1 - 2/V。

Karger's algorithm每個步驟選擇的邊，都必須不是最小割的邊，最後才能得到正確的最小割。選對的機率是1 - 2/V。

每個步驟都會減少一個點，推得正確率是[1-2/V] ⋅ [1-2/(V-1)] ⋅ … ⋅ [1-2/4] ⋅ [1-2/3] = 1/C(V,2) = Ω(1/V²) = Ω(V⁻²)。

根據這個正確率，只要實施V²次以上的Karger's algorithm，結果就相當準確了！