Data - 演算法筆記

Measure

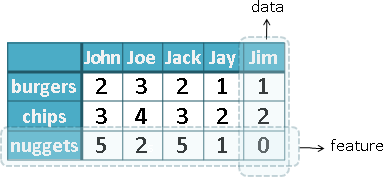
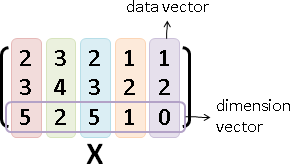
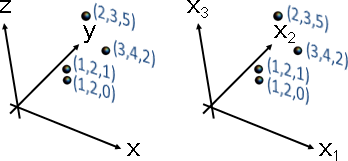
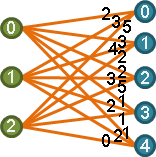
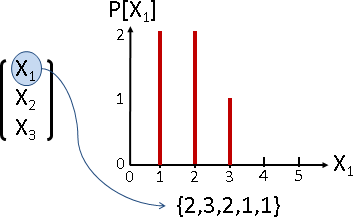
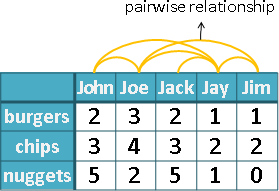
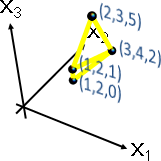
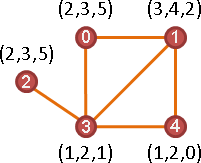
長度（Length）

現實世界，考慮一個東西有多少份量；化為數學，就是考慮一個東西的長度是多少。

此處的長度，是數學術語，不是物理學術語。此處的長度，是指份量多寡，不是指公分公尺。

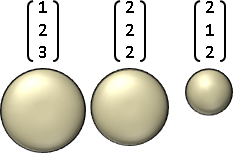
長度函數（Norm）

長度在數學中擁有嚴謹定義：

一、長度不會是負數。p(A) ≥ 0
二、恰是零的東西，長度等於零。p(A) = 0 when A = 0
三、不是零的東西，長度大於零。p(A) > 0 when A ≠ 0
四、一個東西均勻放大縮小，其長度也隨著放大縮小。p(k⋅A) = |k|⋅p(A)
五、兩個東西拼裝起來，其長度只會累加或短少。p(A + B) ≤ p(A) + p(B)

常見的長度函數：

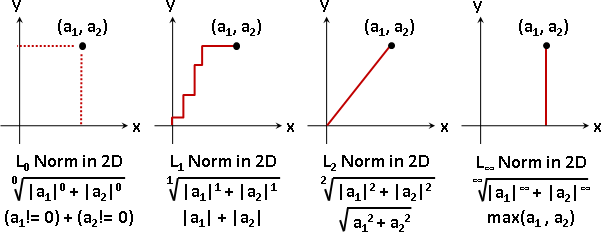
L₀ Norm：非零的數量。
L₁ Norm：先轉正數、再相加。
L₂ Norm：先平方和、再平方根。
L∞ Norm：最大值。

常見的元件：

一個數值的長度：用絕對值計算長度。
一個向量的長度：有多種公式，請參考「Vector Norm」。
　　　　　　　　最經典的是平方長度：先平方和、再平方根。
一個矩陣的長度：有多種公式，請參考「Matrix Norm」。

長度函數（Rank）

不滿足上述定義的長度函數，嚴謹起見，大家另起一名rank。實務上相當罕用。

常見的元件：

一個集合的長度：「Set Rank」
一個矩陣的長度：「Matrix Rank」
一張圖的長度：「Graph Rank」

距離（Distance）

現實世界，考慮兩個東西有多相似；化為數學，就是考慮兩個東西的距離有多接近。

此處的距離，是數學術語，不是物理學術語。此處的距離，是指差異份量多寡，不是指公分公尺。

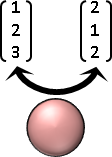
距離函數（Metric）

距離在數學中擁有嚴謹定義：

一、距離不會是負數。d(A,B) ≥ 0
二、兩個相同的東西，距離等於零。d(A,B) = 0 when A = B
三、兩個不同的東西，距離大於零。d(A,B) > 0 when A ≠ B
四、A到B的距離等於B到A的距離。d(A,B) = d(B,A)
五、三角不等式，ABC三個東西，兩邊和大於等於第三邊。
　　d(A,B) + d(B,C) ≥ d(A,C)
　　或者說，三個東西融合成兩個東西，其距離只會累加或短少。
　　d(A,C) ≤ d(A,B) + d(B,C)

常見的距離函數：

Euclidean Distance（L₂）：直線距離。
Taxicab Distance（L₁）：垂直、水平移動的距離。
Hamming Distance（L₀）：相對應維度，數值相異的維度個數。

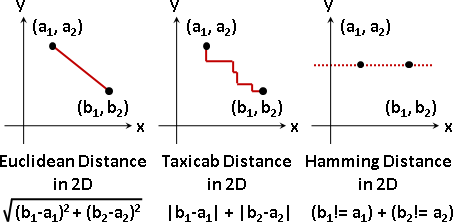
常見的元件：

兩個數值的距離：用減法與絕對值計算距離。
兩個向量的距離：「Minkowski Distance」或者「Angular Distance」
兩串數列的距離：數列類似向量，同上。
兩串字串的距離：「Edit Distance」或者「K-mer Distance」
兩串訊號的距離：以「Linear Predictive Coding」或者「Fourier Transform」
　　　　　　　　重新表示訊號，再用數學公式計算距離。
兩個樣本的距離：「Mahalanobis Distance」
兩個集合的距離：「Jaccard Index」或者「Sørensen–Dice Index」
兩群點的距離：「Hausdorff Distance」或者「Matching Distance」
兩條曲線的距離：「Fréchet Distance」
兩個浮動數字的距離：「Kantorovich Distance」
兩棵樹的距離：「Tree Edit Distance」
兩張圖的距離：「Graph Kernel」

UVa 10508 11085 ICPC 5132

距離函數（Divergence）

不滿足上述定義的距離函數，嚴謹起見，大家另起一名divergence。由於該詞彙已經用於多變量函數的散度運算，簡單起見，大家經常假借舊名distance。

常見的元件：

兩個向量的距離：「Cosine Distance」
兩個函數點（凸函數）的距離：「Bregman Divergence」
兩個浮動數字的距離：「Kullback–Leibler Divergence」或者「Łukaszyk–Karmowski Distance」

半長度函數（Seminorm）、半距離函數（Semimetric）

二、恰是零的東西，長度等於零。p(A) = 0 when A = 0
三、不是零的東西，長度大於零。p(A) > 0 when A ≠ 0

二、兩個相同的東西，距離等於零。d(A,B) = 0 when A = B
三、兩個不同的東西，距離大於零。d(A,B) > 0 when A ≠ B

規則三用來確保：只有零元素的長度是零、只有相同元素的距離是零。然而規則三往往不切實際。數學家將規則三改成大於等於，將名稱添上「半semi」字，意義等同於線性代數的半正定。

規則三改成大於等於，等同於取消規則三。當規則一二同時成立，自然得到新規則三，不必特地寫下來。

另外還有許多修改規則的方式，將名稱添上各式各樣的字眼。為賦新詞強說愁，就不贅述了。