Cycle / Chord / Hole / Triangle

「環」是串成一圈的路線，沒有重複的點。

「弦」是環上不相鄰兩點之間的邊。

「洞」是一種特別的環，沒有弦。

「三角形」是三條邊的環，沒有弦。

ICPC 7661

Chordal Graph（Monotone Transitive Graph）

「弦圖」。多於三條邊的環，必有弦。

換句話說，多於三條邊的洞，必不存在。

弦圖的定義，隱含著遞迴。一個環，從弦切開，形成兩個環，仍需要遞迴切開。所有環切碎成三角形。一個環可以同時切開多處。

弦圖的外觀，宛如許多三角形交錯疊合，附帶許多樹、許多鏈。

學過「三角剖分」的讀者要特別當心，三角剖分通常不是弦圖。

弦圖隨便刪除幾個點（以及連帶的邊），仍是弦圖。換句話說，弦圖的導出子圖是弦圖。

森林、有向無環圖、二分圖、弦圖，都具有這種遞歸性質。

楔子

「有向無環圖」擁有「拓樸順序」。反之亦然。
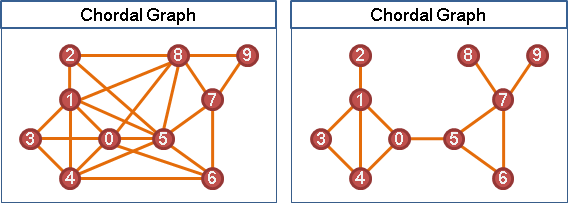
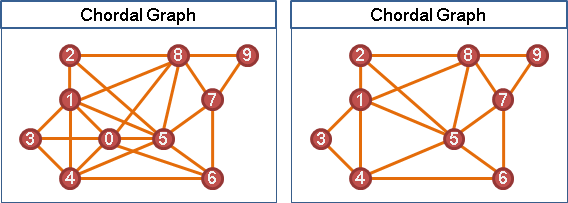
「弦圖」擁有「完美消除順序」。反之亦然。

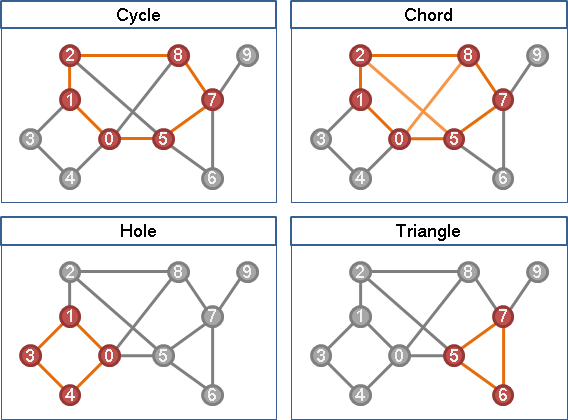
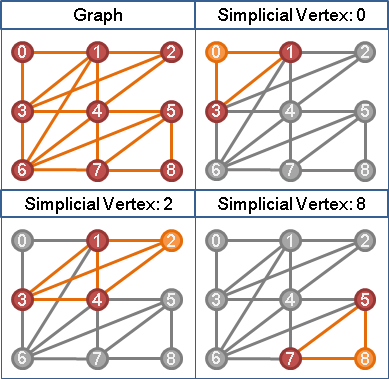
Simplicial Vertex【註：古代名稱，今日看來詞不達意。】

「單體點」。該點的所有鄰居，之間必有邊。

換句話說，該點的所有鄰居，形成團。

換句話說，該點暨所有鄰居，形成極大團。

Perfect Elimination Ordering

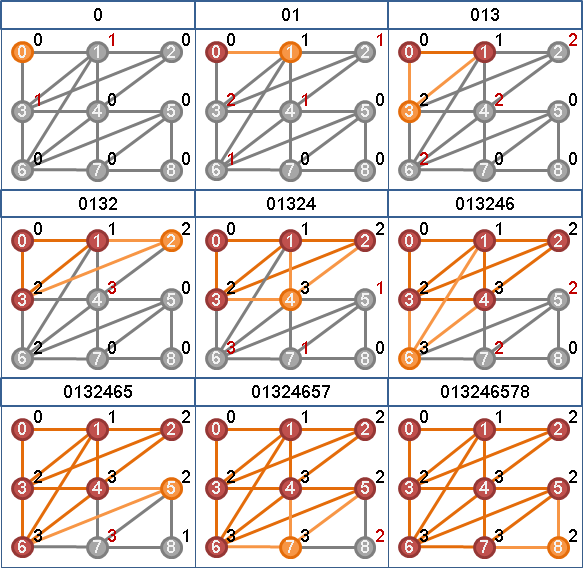
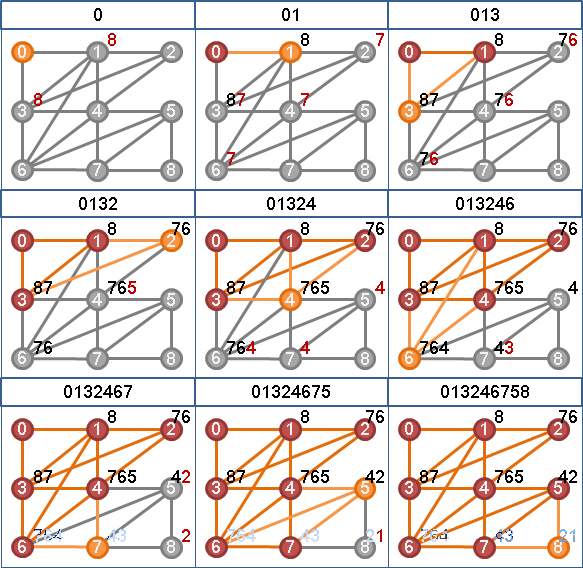
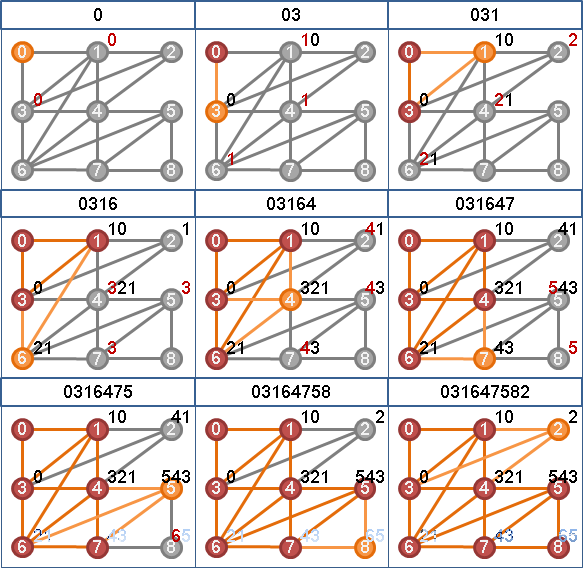
「完美消除順序」。逐次刪除當下的任意一個單體點，所得到的順序。通常有許多種。

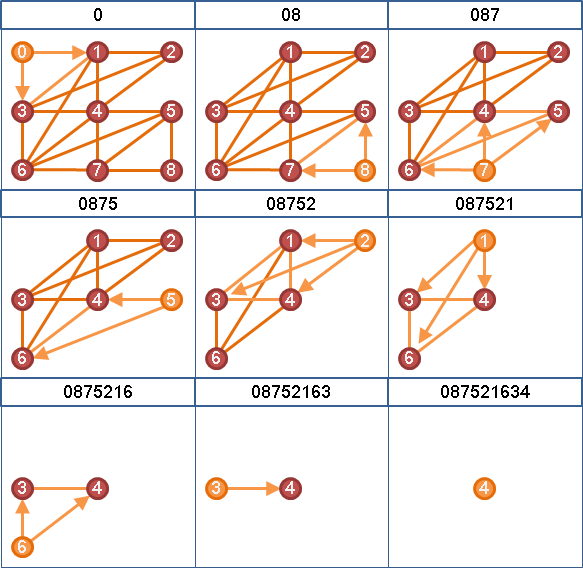
刪除單體點，擁有諸多意義：

一、單體點所屬的極大團的大小減一。

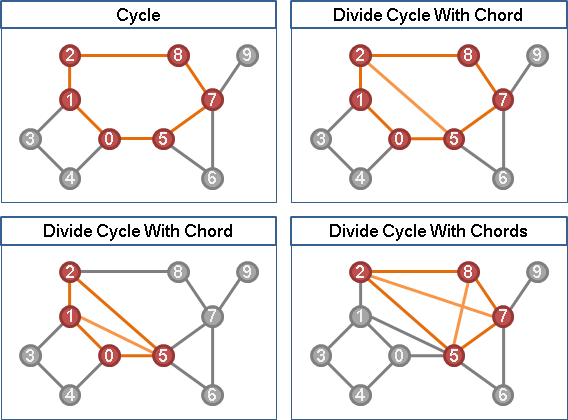
二、單體點的鄰邊們，視作弦。單體點所屬的環們，從弦切開。環被削去一角，留下弦。

三、單體點i，鄰居j，鄰居k，形成三角形ijk。邊ji暨邊ik繞遠路，邊jk抄近路。刪除遠路，保留近路。

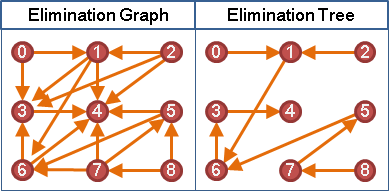
Elimination Graph / Elimination Tree

「消除圖」。完美消除順序可以畫成有向圖。

每個單體點源自哪個團。

「消除樹」。完美消除順序可以畫成有向森林。

當前點的父親，是順序更大、順序最早的鄰居。

時間複雜度等於一次Graph Traversal的時間。

const int V = 10; // 點數 vector<int> adj[V]; // adjacency lists int order[V]; // perfect elimination ordering int visit[V]; // 每個點的最佳刪除順序編號 vector<int> trace[V]; // elimination graph int parent[V]; // elimination tree vector<int> child[V]; // elimination tree void elimination_graph() { for (int i=0; i<V; ++i) visit[order[i]] = i; for (int i=0; i<V; ++i) trace[i].clear(); for (int i=0; i<V; ++i) { int a = order[i]; // 當前點 for (int k=0; k<adj[a].size(); ++k) { // 鄰居 int v = adj[a][k]; // 順序更大的鄰居 if (visit[v] > visit[a]) trace[a].push_back(v); } } } void elimination_tree() { for (int i=0; i<V; ++i) visit[order[i]] = i; for (int i=0; i<V; ++i) parent[i] = -1; for (int i=0; i<V; ++i) child[i].clear(); for (int i=0; i<V; ++i) { int a = order[i]; // 當前點 int b = -1, visit_b = 1e9; // 父親、順序編號 for (int k=0; k<adj[a].size(); ++k) { // 鄰居 int v = adj[a][k]; // 順序更大、順序最早的鄰居 if (visit[v] > visit[a] && visit[v] < visit_b) { b = v; visit_b = visit[b]; } } if (b == -1) continue; // 不連通 parent[a] = b; child[b].push_back(a); } }

Perfect Elimination Ordering Testing

檢查一個順序是不是完美消除順序。

一、遞增法。時間複雜度O(V³)。

依序掃描，逐一檢查是否為單體點。檢查所有鄰居是否為團──鄰居之間所有點對，必須都有邊。

const int V = 10; // 點數 bool adj[V][V]; // adjacency matrix int order[V]; // ordering bool graph[V]; // 剩餘點所形成的圖 bool peo_test() { for (int i=0; i<V; ++i) graph[i] = true; for (int i=0; i<V; ++i) { int a = order[i]; graph[a] = false; for (int p=0; p<V; ++p) if (graph[p] && adj[a][p]) for (int q=p+1; q<V; ++q) if (graph[q] && adj[a][q]) if (!adj[p][q]) return false; } return true; }

二、遞推法。時間複雜度O(V+E)。

反向掃描，逐一檢查是否為單體點。

當前點a，鄰居b，鄰居取順序更大、順序最早者。b已是單體點，b已是團。想要確認a是否形成團，只需檢查a點與b團之間的邊──「a的鄰居」必須包含於「b暨鄰居」。

簡單來說，檢查消除樹每一對父子──在消除圖上，「子的鄰居」必須包含於「父暨鄰居」。

窮舉時，子為主，父為輔。父重複出現，時間複雜度O(V²)。

窮舉時，父為主，子為輔，時間複雜度壓至O(V+E)。

const int V = 10; // 點數 vector<int> adj[V]; // adjacency lists int order[V]; // ordering int visit[V]; // 每個點的最佳刪除順序編號 vector<int> trace[V]; // elimination graph vector<int> child[V]; // elimination tree bool bucket[V]; // bucket sort bool peo_test() { for (int i=0; i<V; ++i) visit[order[i]] = i; for (int i=0; i<V; ++i) trace[i].clear(); for (int i=0; i<V; ++i) child[i].clear(); for (int i=0; i<V; ++i) bucket[i] = false; // 建立消除圖、消除樹 for (int i=0; i<V; ++i) { int a = order[i], b = -1, j = 1e9; for (int k=0; k<adj[a].size(); ++k) { int v = adj[a][k]; if (visit[v] > i) trace[a].push_back(v); if (visit[v] > i && visit[v] < j) j = visit[b = v]; } if (b != -1) child[b].push_back(a); } // 窮舉時，父為主。 for (int i=0; i<V; ++i) { int b = order[i]; // 絕子絕孫 if (child[i].size() == 0) continue; // b暨鄰居（只看順序比b更大的點） bucket[b] = true; for (int k=0; k<trace[b].size(); ++k) { int v = trace[b][k]; bucket[v] = true; } // 窮舉時，子為輔。 for (int i=0; i<child[b].size(); ++i) { int a = child[b]; // a的鄰居（只看順序比a更大的點） for (int k=0; k<trace[a].size(); ++k) { int v = trace[a][k]; if (!bucket[v]) return false; } } // 清除bucket bucket[b] = false; for (int k=0; k<trace[b].size(); ++k) { int v = trace[b][k]; bucket[v] = false; } } return true; }

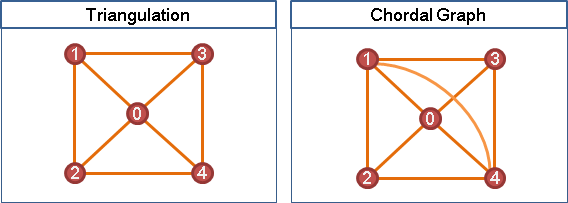
數學證明：弦圖⇔完美消除順序

(⇒)弦圖必有單體點（容後證明）。弦圖隨便刪除一個點，仍是弦圖。弦圖可以遞迴刪除單體點。

(⇐)任意一個多於三條邊的環，此環之中，順序最早的點，稱之v。因為v的所有鄰居必有邊，所以此環必有弦。

數學證明：弦圖必有單體點

證明又臭又長，缺乏實際用途。讀者可以跳過。

每個連通分量都是弦圖，各自處理。方便起見，假設圖連通。

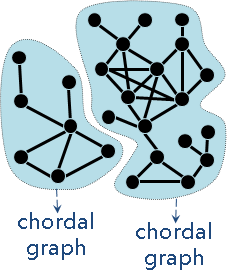
一張圖要嘛是完全圖、要嘛不是完全圖。

如果是完全圖：所有點都是單體點。得證。

如果不是完全圖：有兩點不相鄰。進一步找到「最小點分隔Minimum Vertex Separator」：讓兩點不連通的最小點集合S。

整張圖分離成四個集合ABSR。AB顯然不是空集合。S不是空集合（假設圖連通）。R可能是空集合。

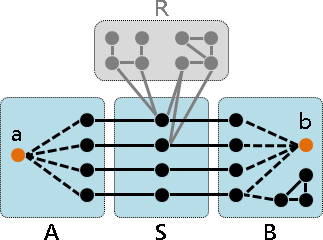
一、S是團。

根據最小點分隔，AB之間無邊，S每一點到AB都有邊。

根據弦圖，S到AB的邊形成環，而AB之間無法有弦，於是AS之間、BS之間必須有弦，於是S之間必須有弦。

二、單體點不可能位於S，只可能位於ABR。

S到AB都有邊，但是AB之間無邊，無法形成團。

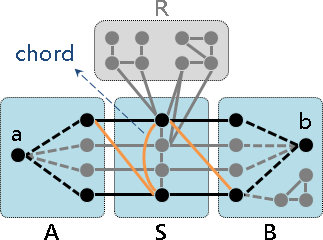
接下來專心考慮單體點可能位於A的情況。

A∪S要嘛是團、要嘛不是團。

如果是團：A的所有點都是單體點。得證。

如果不是團：A∪S有兩點不相鄰。進一步重新找到最小點分隔。整張圖重新分離成四個集合A'B'S'R'。

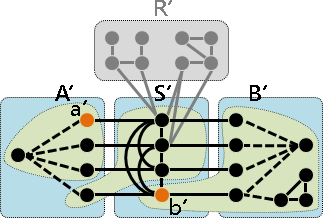
一、A∪S有兩點不相鄰，不可能兩點皆位於S。

因為S是團。

二、新的最小點分隔S'，不會用到B，不會用到R。

其中一點位於A。然而AB之間無邊，AR之間無邊。

三、如果一點在A一點在S，那麼B⊆B'。

（a'∈A、b'∈S、a'∈A'、b'∈B'）

AB之間無邊，SB之間有邊，B將併入B'。

四、如果兩點都位於A，那麼B⊆R'。

（a'∈A、b'∈A、a'∈A'、b'∈B'）

AB之間無邊，B不會併入A'B'。B跟A'B'S'皆不相交，那就只剩R'了。

五、(A'∪S') ⊂ (A∪S)，尺寸變小。

B'至少佔據一點，(A'∪S')至少縮小一點。

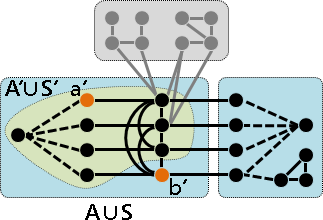
遞迴下去，A'∪S'不斷縮小，直到形成團。最差的情況是A'變成一點。得證。

Chordal Graph Recognition

檢查一張圖是不是弦圖。主要有兩種策略：

一、窮舉多於三條邊的環，檢查弦。總共O(V!)種。

能不能只檢查特定的環呢？事實上可以。請自行上網搜尋資料。

二、窮舉各種順序，檢查是否為完美消除順序。總共V!種。

能不能只檢查特定順序呢？事實上可以。請見下個章節。

楔子

有向無環圖的拓樸順序：特殊BFS順序、DFS逆序
弦圖的完美消除順序：MCS逆序、LexBFS逆序、LexDFS逆序

除了BFS、DFS，再補充三個遍歷演算法MCS、LexBFS、LexDFS，用來找到團。

Maximum Cardinality Search（MCS）

每回合找到一個點，連往已拜訪點的邊數最多。如果很多點同時符合條件，則任選一點。

時間複雜度O(V²)。運用Binary Heap壓至O(V+ElogV)。運用Fibonacci Heap壓至O(E+VlogV)。運用Bucket Sort壓至O(V+E)。

這些加速技巧，也出現在單源最短路徑演算法。請見本站文件「Path」。

補充一下Bucket Sort的時間複雜度分析。隨時紀錄最大值放在哪個桶子。刪除最大值、尋找次大值，只需笨拙地不斷減一，直到遭遇次大值。

邊數總是加一，總共加E。尋找次大值，總共頂多減E。時間複雜度O(V+E)。

Lexicographic Breadth-first Search（LexBFS）

BFS深入考慮細節。仔細安排小孩的拜訪順序：優先擴大團。

i from V-1 to 0
取字串最大的點。
所有未拜訪鄰居，字串尾端添加i。

BFS：優先拜訪深度最小的點。
LexBFS：深度平手時，優先拜訪字串最大的點。
LexBFS-：字串平手時，優先拜訪索引值最小的點。

時間複雜度O(V²)。運用Bucket Sort壓至O(V+E)。

Lexicographic Depth-first Search（LexDFS）

DFS深入考慮細節。仔細安排子孫的拜訪順序：優先擴大團。

i from 0 to V-1
取字串最大的點。
所有未拜訪鄰居，字串開頭添加i。

DFS：優先拜訪深度最大的點。
LexDFS：深度平手時，優先拜訪字串最大的點。
LexDFS+：字串平手時，優先拜訪索引值最大的點。

時間複雜度O(V²)。運用Binary Heap壓至O(V+ElogV)。運用vEB Tree壓至O(V+EloglogV)。

數學證明：弦圖⇔ MCS逆序是完美消除順序

(⇒)遞迴刪除單體點：

一、遍歷過程，不受未拜訪點的影響。因此，一張圖刪除最後一個拜訪的點，重新實施遍歷演算法，遍歷順序依然相同。

二、遍歷過程，優先擴大團。因此，最後一個拜訪的點，必是極大團的點，必是單體點。

(⇐)先前章節提過，完美消除順序必得弦圖。

MCS逆序、LexBFS逆序、LexDFS逆序，三者皆是如此。

Chordal Graph Recognition

判斷弦圖，只需針對特定順序，無須窮舉各種順序。

MCS逆序、LexBFS逆序、LexDFS逆序，檢查是否為完美消除順序。挑一種檢查即可。

ICPC 2424 6308

延伸閱讀：各種遍歷演算法的關聯

       GEN
      / | \
   BFS MNS DFS
    | / | \ |
LexBFS MCS LexDFS

MNS系統可以用來找到完美消除順序。

Interval Graph

(G == interval) iff (G == chordal && ~G == comparability)
if (G == interval) then (G == chordal)
if (G == interval) then (~G == comparability)

ICPC 2326

Circular-arc Graph

ICPC 4274

Split Graph

(G == split) iff (G == chordal && ~G == chordal)
(G == split and G == permutation) iff (G == interval and ~G == interval) 

延伸閱讀：弦圖推廣成有向圖

我不清楚是否有人研究。「弦」可能有兩種定義：

一、一個有向環，不相鄰兩點之間的有向邊。

二、一雙有向路徑，橫跨路徑的有向邊。

一個有向環，從弦切開，形成一個有向環、一雙有向路徑。只能遞迴其中一邊。怪怪的。

一雙有向路徑，從弦切開，形成兩雙有向路徑，但是重疊於弦。怪怪的。

延伸閱讀：完美消除順序推廣成有向圖

修改單體點的定義：該點若有入邊ji與出邊ik，則必有邊jk。

「單調遞移圖Monotone Transitive Graph」就是擁有「完美消除順序」的圖。反之亦然？【尚待確認】

Chain Graph

二分圖，X群（Y群）存在一種點順序：當前點的鄰居，包含之後所有點的鄰居。

(G == chain) iff (G == bipartite && C(G) == chordal)
C(G): make X and Y cliques

《Computing the Minimum Fill-In is NP-Complete》

Strongly Chordal Graph