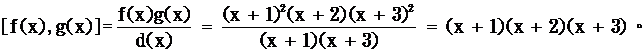§ 3-3:最大公因式與最小公倍式
![]()
L.C.M與H.C.M的求法
(一)、最大公因式的求法
a. 因式分解法:
將各個多項式分別因式分解,再取其中公因式相乘,即可得到H.C.F。
舉例說明:![]()
![]()
所以(f(x),g(x))=(x+1)(x+3)
b.輾轉相除法:
設f(x),g(x)為二多項式,且g(x)¹0,則由除法定理可知:恰有兩個多項式q(x),r(x)滿足f(x)=g(x)×q(x)+r(x),其中r(x)=0或deg r(x)<deg g(x)。
c.因式的性質:
若設d(x)|f(x),d(x)|g(x),則d(x)|m(x)×f(x)+n(x)×g(x)。
(一)、最小公倍式求法
a.因式分解法:
先將各多項式因式分解,再取出最低公倍式。
舉例說明:![]()
![]()
[f(x),g(x)]=(x+1)(x+2)(x+3)
b.先求出最大公因式:
求出f(x)與g(x)的最大公因式為d(x),再由性質c的第三點求出,意即L.C.M=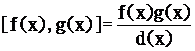 。
。
舉例說明:
![]()
![]()
(f(x),g(x))=(x+1)(x+3)
所以