主題 1. 不定積分和定積分
不定積分
Python 的函數是:integrate(f(x), x)
本章第一節範例5求解不定積分
Python的模組和語法如下import math
from sympy import *
x = symbols('x')
integrate(exp(2*x), x)
Out[1]: exp(2*x)/2
Python不定積分不會出現一個任意常數C,這點讀者必須自行處理。
其次,定積分
Python的函數是:integrate(f(x), (x,a,b))
承前題
,Python的模組和語法如下
import math
from sympy import *
x = symbols('x')
integrate(exp(2*x), (x, 0, 1))
Out[2]: -1/2 + exp(2)/2主題 2. 積分方法
2-1 變數代換法
2-2 分部積分法
2-3 部分分式
2-4 多重積分
2-5 瑕積分
2-1. 變數代換法
求解不定積分
Python的模組和語法如下import math
from sympy import *
x = symbols('x')
integrate(x**3*exp(x**4+2), x)
Out[4]: exp(x**4 + 2)/4
求解不定積分
Python的語法如下
integrate(2*x/(x**2-1), x)
Out[5]: log(x**2 - 1)求解不定積分
Python的語法如下
integrate(1/(x*log(x)*log(log(x))), x)
Out[6]: log(log(log(x)))
需注意,當解出現對數時,Python不會自動加上絕對值,我們必須知道這一點。
如前章提及Python不定積分不會出現一個任意常數C,這點讀者可以自行處理。
求解定積分
這個定積分就有一些複雜,直接寫被積函數無法解出來
例如
執行integrate((x+2)/sqrt(2*x+1), (x, 0, 4))會出現求解失敗的訊息。如果根據書本解的方式,改用代換過與換界的u函數,則就順利。如下integrate((x**2/2+3/2), (x, 1, 3)) #符號還是可以用x不需要換成u
Out[8]: 7.33333333333333 #分式答案22/3
另一個解法是用模組scipy內的scipy.integrate內的函數quad(),如下:
from scipy.integrate import quad
def f(x):
return (x+2)/sqrt(2*x+1)quad(f, 0,4)
Out[9]: (7.333333333333334, 5.321163202449652e-10)
Out[9]內,第一個數字就是22/3,第2個數字是數值積分的誤差。從此處可以看到,Python模組各有各自的問題,所以遇到問題,要嘗試多方的工具。
我們再繼續看範例。
求解定積分
這題定積分就很順利
integrate(sqrt(x)/((9-x*sqrt(x))**2), (x, 1, 4))
Out[11]: 7/12
2-2 分部積分法
求解定積分
integrate((x**2)*exp(-x), (x, 0, 7))
Out[12]: -65*exp(-7) + 2求解定積分定積分
integrate((x**3)*(log(x))**2, (x, 1, 2))
Out[13]: -2*log(2) + 15/32 + 4*log(2)**2
2-3 部分分式型
求解定積分不定積分
integrate((3*x**3-18*x**2+29*x-4)/((x+1)*((x-2)**3)))
Out[14]: (3*x - 7)/(x**2 - 4*x + 4) + log(x - 2) + 2*log(x + 1)
2-4 多重積分
再來就是多重積分。求解二重積分
,這個範例的積分邊界都是常數,
from sympy import *
x, y = symbols("x y")
f = (10*x*y**2)
integrate(f, (x, -1, 2), (y, 3, 6)) #
Out[15]: 945求解二重積分
,這個範例的積分邊界一個是變數,
from sympy import *
x, y = symbols("x y")
f = x* y ** 2
integrate(f, (y, x**2, x), (x, 0, 1))
Out[16]: 1/40
2-5 瑕積分
瑕積分需要用到無限大符號,sympy 的無限大符號是兩個小寫的英文字母o,也就是oo求解瑕積分
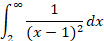
integrate(1/(x-1)**2, (x, 2, oo))
Out[68]: 1
此積分收斂且值為1求解瑕積分2
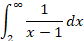
integrate(1/(x-1), (x, 2, oo))
Out[69]: oo
結果是發散