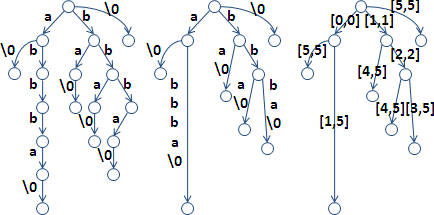運用後綴處理字串搜尋問題

兩步驟：枚舉T的所有後綴、搜尋開頭恰為P的後綴。

T: mississippi
P: issi

all suffixes of T:
   mississippi, ississippi, ssissippi, ...
   
string searching:
   0             1            2
   mississippi   ississippi   ssissippi   ...
   issi          issi         issi

儲存大量後綴的資料結構

以大量字串的資料結構，儲存並排序T的全部後綴，就更容易搜尋後綴。例如Array、Binary Tree、Trie、Automaton。

後綴們有許多重複字元。精簡重複字元、減少空間大小、改善排序速度。

                  build    string searching
----------------- -------- ---------------
suffix array      O(T+A)   O(PlogT)
 + lcp array      O(T+A)   O(P+logT)
suffix trie       O(T²)    O(P)
suffix tree       O(T)     O(P)
suffix automata   O(TA)    O(P)

演算法選擇

適用情況：P為定值，T為變動值。
單一字串搜尋：Morris–Pratt Algorithm、Boyer–Moore Algorithm。
多重字串搜尋：Aho–Corasick Algorithm。

適用情況：T為定值，P為變動值。
單一、多重字串搜尋：Suffix Array、Suffix Trie、Suffix Tree。

Suffix Array

「後綴陣列」。一個字串的全部後綴，統統放入陣列。排序所有後綴，以利之後搜尋。

一個索引值表示一個後綴，空間複雜度O(T)。

string:
   mississippi

all suffixes:
   mississippi, ississippi, ssissippi, sissippi, issippi,
   ssippi, sippi, ippi, ppi, pi, i

suffix array:
   +---+------+---------+------------+-------------+-     -+
   | i | ippi | issippi | ississippi | mississippi |  ...  |
   +---+------+---------+------------+-------------+-     -+

suffix array:
   +---------+--------+--------+--------+-     -+
   | [10,10] | [7,10] | [4,10] | [1,10] |  ...  |
   +---------+--------+--------+--------+-     -+

suffix array:
   +----+---+---+---+---+---+---+---+---+---+---+
   | 10 | 7 | 4 | 1 | 0 | 9 | 8 | 6 | 3 | 5 | 2 |
   +----+---+---+---+---+---+---+---+---+---+---+

suffix array:
     | sa | suffix
  ---+----+------------
   0 | 10 | i
   1 |  7 | ippi
   2 |  4 | issippi
   3 |  1 | ississippi
   4 |  0 | mississippi
   5 |  9 | pi
   6 |  8 | ppi
   7 |  6 | sippi
   8 |  3 | sissippi
   9 |  5 | ssippi
  10 |  2 | ssissippi

suffix array:
   +------------------------+
   | 10 7 4 1 0 9 8 6 3 5 2 |
   +------------------------+
      i i i i m p p s s s s
        p s s i i p i i s s
        p s s s   i p s i i 
        i i i s     p s p s
          p s i     i i p s
          p s s       p i i
          i i s       p   p
            p i       i   p
            p p           i
            i p
              i

演算法（Quicksort）

以快速排序法排序所有後綴。每個後綴的長度都不同，名次必不同，毋須特地使用stable sort。

兩個後綴比大小需時O(T)，兩兩比較次數是O(TlogT)，時間複雜度O(T²logT)。

char t[11+1] = "mississippi"; int sa[11]; // t的後綴陣列 bool cmp(int& i, int& j) { return strcmp(&t[i], &t[j]) < 0; } void suffix_array() { for (int i=0; i<11; ++i) sa[i] = i; sort(sa, sa+11, cmp); } char t[11+1] = "mississippi"; char* sa[11]; // 用指標代替索引值 bool cmp(char* i, char* j) { return strcmp(i, j) < 0; } void suffix_array() { for (int i=0; i<11; ++i) sa[i] = t + i; sort(sa, sa+11, cmp); }

演算法（Radix Sort）

字元種類有限、範圍有限，適用Radix Sort。時間複雜度O((T+A) ⋅ T)。A是字元種類數目。

演算法（Prefix-doubling Algorithm）

Radix Sort和Prefix-doubling Algorithm有些相似。

Radix Sort：各回合拿倒數第一個、倒數第二個、倒數第三個、……字元實施排序，總共T回合。每回合採用Counting Sort。

Prefix-doubling Algorithm：各回合拿前一個、前二個、前四個、前八個、……字元實施排序，總共logT回合。每回合可以採用Quicksort或Counting Sort。

運用上回合的排序結果，先比前半段、再比後半段，不必逐個字元比較。用一個字元的排序結果，拼成兩個字元的排序結果；用兩個字元的排序結果，拼成四個字元的排序結果；以此類推。

每回合採用Quicksort，時間複雜度O(logT ⋅ TlogT) = O(Tlog²T)。

char t[11+1] = "mississippi"; int sa[11]; int temp[2][11]; struct CMP { int* rank, n, N; bool operator()(int i, int j) { // 先比前半段 if (rank[i] != rank[j]) return rank[i] < rank[j]; // 再比後半段 int a = (i+n<N) ? rank[i+n] : -1; int b = (j+n<N) ? rank[j+n] : -1; return a < b; } }; void suffix_array() { int N = 11; // 字串長度 int* rank = temp[0]; int* new_rank = temp[1]; /* 第一回合：字元個數為1。 */ // 各個名次對應的後綴 // 投機取巧：隨便初始化，待會就重算。 for (int i=0; i<N; i++) sa[i] = i; // 各個後綴對應的名次 // 投機取巧：ASCII數值當作名次。 for (int i=0; i<N; i++) rank[i] = t[i]; /* 第二回合以降：字元個數為2，不斷倍增。 */ // for (int m=2; m/2<N; m*=2) for (int n=1; n<N; n*=2) { // 運用上回合的名次，排序所有後綴。 // 每個後綴，拿前m個字元，先比前半段、再比後半段。 // CMP cmp = {rank, m/2, N}; CMP cmp = {rank, n, N}; sort(sa, sa+N, cmp); // 重新排名：相異者，排在相異名次；相同者，排在相同名次。 int r = 0; new_rank[sa[0]] = r; for (int i=1; i<N; i++) { // 相異者，名次加一；相同者，名次一樣。 if (cmp(sa[i-1], sa[i])) r++; // 設定名次。 new_rank[sa[i]] = r; } swap(rank, new_rank); // 如果名次皆相異，表示排序完畢，提早結束演算法。 if (r == N-1) break; } }

每回合採用Counting Sort，時間複雜度降為O(logT ⋅ (T+A))。A是字元種類數目。

char t[11+1] = "mississippi"; int sa[11]; int c[50000]; // counting sort array int temp[2][50000]; void suffix_array() { int N = 11; // 字串長度 int A = 128; // 字元總類 int* rank = temp[0]; int* new_rank = temp[1]; /* 第一回合：字元個數為1。 */ // stable counting sort // 初始化rank和sa for (int i=0; i<A; ++i) c[i] = 0; for (int i=0; i<N; ++i) c[rank[i] = t[i]]++; for (int i=1; i<A; ++i) c[i] += c[i-1]; for (int i=N-1; i>=0; --i) sa[--c[t[i]]] = i; /* 第二回合以降：字元個數為2，不斷倍增。 */ // for (int m=2; m/2<N; m*=2) for (int n=1; n<N; n*=2) { // counting sort：套用上回合的rank。 for (int i=0; i<A; ++i) c[i] = 0; for (int i=0; i<N; ++i) c[rank[i]]++; for (int i=1; i<A; ++i) c[i] += c[i-1]; // 前半段次序：上回合已計算，不必重算。 // for (int i=N-1; i>=0; --i) // sa[--c[rank[i]]] = i; // 後半段次序：採用前半段次序，另外考慮空字串。 int* sa2 = new_rank; // 借用記憶體、節省記憶體 int r = 0; // 名次 for (int i=N-n; i<N; ++i) // 空字串，名次最小 sa2[r++] = i; // 索引值由小到大排名 for (int i=0; i<N; ++i) // 其餘部分等同前半段次序 if (sa[i] >= n) // 有前半段，才有後半段 sa2[r++] = sa[i] - n; // counting sort：前半段次序一樣者，按照後半段次序擷取。 // 本回合的sa for (int i=N-1; i>=0; --i) sa[--c[rank[sa2[i]]]] = sa2[i]; // 本回合的rank new_rank[sa[0]] = r = 0; for (int i=1; i<N; ++i) { // 相異者，排在相異名次；相同者，排在相同名次。 if (!(rank[sa[i-1]] == rank[sa[i]] && sa[i-1]+n < N && // stable sort trick rank[sa[i-1]+n] == rank[sa[i]+n])) r++; new_rank[sa[i]] = r; } swap(rank, new_rank); // 如果名次皆相異，表示排序完畢，提早結束演算法。 if (r == N-1) break; // 修正counting sort數值範圍 A = r + 1; } }

演算法（DC3）

全部後綴分成三類，分別處理。

一、全部後綴根據「所在位置」分成兩堆：
　　所在位置除以三，餘零者為S0，餘一或二者為S12。
二、用Radix Sort排序S12，僅排序前三個字元。
　　平手時，才繼續排序下三個字元。
　　途中可以隨時利用已經排序好的部份。
三、利用排序完畢的S12，來排序S0。
四、合併S12與S0。

時間複雜度O(T+A)。

演算法（SA-IS）

全部後綴分成三類，分別處理。

一、全部後綴以「所在位置」與「字典順序」分成兩堆：
　甲、右方後綴字典順序更小為S、右方後綴字典順序更大為L。
　乙、連續的S的左邊第一個為LMS。
二、用Radix Sort排序LMS。
　　途中可以隨時利用已經排序好的部份。
三、利用排序完畢的LMS，來排序完整的後綴陣列。

時間複雜度O(T+A)。實務上最快的演算法。

字串搜尋

已排序陣列，使用Binary Search。時間複雜度O(PlogT)。

char t[11+1] = "mississippi"; char p[4+1] = "issi"; int sa[11]; // t的後綴陣列 // 小心，此寫法是編譯器未定義行為。 // i不見得是陣列數值，j不見得是搜尋數值。 bool cmp2(int& i, int j) { return strncmp(&t[i], &p[j], 4) < 0; } void string_searching() { suffix_array(); auto it = lower_bound(sa, sa+11, 0, cmp2); if (it == sa+11 || strncmp(&t[*it], &p[0], 4)) cout << "找不到"; else cout << "T的第" << *it << "個字元開始為P"; } char t[11+1] = "mississippi"; char p[4+1] = "issi"; char* sa[11]; // 用指標代替索引值 // 小心，此寫法是編譯器未定義行為。 // i不見得是陣列數值，j不見得是搜尋數值。 bool cmp2(char* i, const char* j) { return strncmp(i, j, 4) < 0; } void string_searching() { suffix_array(); auto it = lower_bound(sa, sa+11, p, cmp2); if (it == sa+11 || strncmp(*it, p, 4)) cout << "找不到"; else cout << "T的第" << (*it - t) << "個字元開始為P"; }

大量字串搜尋

將所有T連成一串，以'\0'隔開，然後建立後綴陣列。每個P分別做二元搜尋。

想讓排序結果正確，隔開字元的字典順序必須小於T的每個字元。大家習慣用'\0'。

UVa 10526 10580

Longest Common Prefix

一堆字串的「最長共同前綴」只有一個，有可能是空字串。

演算法很簡單：字串們一齊從頭開始比對字元。

s1: aabbccc
s2: aabbbccc
s3: aabaccc

s1 s2 s3 的 LCP 就是 aab。

兩個後綴的LCP

string:
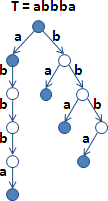
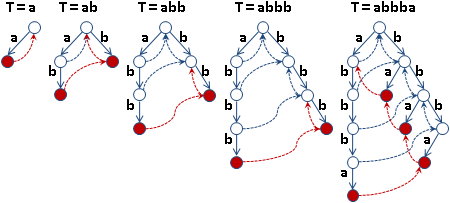
   abbbababba

suffixes:
   s0: abbbababba
   s1: bbbababba
   s2: bbababba
       ......
   s8: ba
   s9: a

LCP(s1, s2) = bb
LCP(s0, s9) = a

兩個後綴的LCP，
就是排序全部後綴之後，兩個後綴之間的所有後綴的LCP。

     0 1 2 3 4 5 6 7 8 9
   +---------------------+
sa | 9 4 6 0 8 3 5 7 2 1 |
   +---------------------+
     a a a a b b b b b b
       b b b a a a b b b
       a b b   b b a a b
       b a b   a b   b a
       b   a   b a   a b
       a   b   b     b a
           a   a     b b
           b         a b
           b           a
           a

LCP(7th, 9th) = LCP(7th, 8th, 9th) = LCP(s7, s2, s1) = bb
LCP(4th, 8th) = LCP(4th, ..., 8th) = LCP(s8, s3, s5, s7, s2) = b

開頭相近的後綴，排在一起；開頭不相近的後綴，被開頭相近的後綴隔開。

排序全部後綴之後，兩個後綴之間的所有後綴的LCP，
就是兩兩相鄰後綴的LCP們的LCP。

LCP(7th, 9th) = LCP( LCP(7th, 8th), LCP(8th, 9th) ) = bb
LCP(4th, 8th) = LCP( LCP(4th, 5th), ..., LCP(7th, 8th) ) = b

以相鄰後綴的LCP，推導出任意後綴的LCP。

兩兩相鄰後綴的LCP，表達成數值：
Longest Common Prefix Array

直接記錄LCP字串，浪費大量記憶體空間，因而改為記錄LCP長度。輔以原字串、後綴陣列，便可得到LCP字串。

排序全部後綴之後，每一個後綴與前一個後綴的LCP長度，儲存於陣列，得到LCP Array。

       0 1 2 3 4 5 6 7 8 9
     +---------------------+
  sa | 9 4 6 0 8 3 5 7 2 1 |
     +---------------------+
lcpa | 0 1 2 3 0 2 3 1 3 2 |
     +---------------------+
       a a a a b b b b b b
         b b b a a a b b b
         a b b   b b a a b
         b a b   a b   b a
         b   a   b a   a b
         a   b   b     b a
             a   a     b b
             b         a b
             b           a
             a

LCP_length(7th, 9th) = min(lcpa[7+1], ..., lcpa[9]) = 2
LCP_length(4th, 8th) = min(lcpa[4+1], ..., lcpa[8]) = 1

兩個後綴的LCP，藉由LCP Array，變成了查詢區間最小值。請參考「偽線段樹」。

UVa 12338

演算法

依序計算兩兩相鄰後綴的LCP，依序填寫LCP Array。時間複雜度O(T²)。

char s[10 + 1]; // string int sa[10]; // suffix array，各個名次對應的後綴。 int lcpa[10]; // longest common prefix array int lcp_length(char* s, char* t) { int n = 0; while (s[n] && t[n] && s[n] == t[n]) n++; return n; } void lcp_array() { lcpa[0] = 0; for (int i=1; i<N; i++) lcpa[i] = lcp_length(s+sa[i], s+sa[i-1]); }

演算法

運用小技巧，建立LCP Array僅需時O(T)。

一個字串的後綴，開頭去掉一個字元，仍是後綴。

兩個相鄰後綴，開頭各去掉一個字元，得到兩個新後綴。雖然不見得相鄰，但是大小關係依然相同。LCP則少了一個開頭字元。

           2 3       7   9
      ---------------------
           a a       b   b
           b b       b   b
           b b       a   b
           a b           a
             a           b
             b           a
             a           b
             b           b
             b           a
             a

abba < abbbababba            => bba < bbbababba
LCP(abba, abbbababba)        =  a + LCP(bba, bbbababba)
LCP_length(abba, abbbababba) =  1 + LCP_length(bba, bbbababba)

兩個新後綴的LCP長度，小於等於第二個新後綴、與其前方相鄰後綴的LCP長度。

LCP_length(2th, 3th) - 1 = LCP_length(7th, 9th) ≤ LCP_length(7th, 8th)
LCP_length(3-1th, 3th) - 1 ≤ LCP_length(8-1th, 8th)

從最長的後綴（原字串）開始，逐次去掉開頭字元，跳著填寫LCP Array。

3th: abbbababba     9th: bbbababba      8th: bbababba
LCP(3-1th, 3th) --> LCP(9-1th, 9th) --> LCP(8-1th, 8th) --> ...

每次LCP減少一個開頭字元之後，新後綴與其相鄰後綴的LCP只會一樣長、更長。不必每次從頭開始比對字元。

一、依序掃描原字串的每個後綴。每次都會少掉一個開頭字元：
　甲、求得該後綴在後綴陣列裡的位置。
　乙、再找出上一個相鄰後綴。
　丙、逐一比對字元，求出LCP長度，儲存於LCP Array。
　丁、下次就可以從LCP長度減一開始比對字元。小心不能減至負值。

char s[10 + 1]; // string int sa[10]; // suffix array，各個名次對應的後綴。 int rank[10]; // 各個後綴對應的名次 int lcpa[10]; // longest common prefix array void lcp_array() { // 也就是各個後綴在sa當中的索引值 // 也就是sa的反函數 for (int i=0; i<10; ++i) rank[sa[i]] = i; for (int i=0, lcp=0; i<10; i++) if (rank[i] == 0) lcpa[0] = 0; else { int j = sa[rank[i]-1]; if (lcp > 0) lcp--; while (s[i+lcp] == s[j+lcp]) lcp++; lcpa[rank[i]] = lcp; } }

字串搜尋

一、T的Suffix Array。O(T+A)。
二、T的LCP Array。O(T)。
三、LCP Array的偽線段樹。建立O(T)、搜尋O(logT)。
　　用來快速求得LCP(i,j)。
四、二元搜尋。

令二元搜尋的三個指標是L M R。二元搜尋的過程是：逐字比對P與M，判斷P < M或者P > M，讓M' = L或者M' = R。時間複雜度O(PlogT)。

M與L R經常有共同前綴。P與M比大小，可以從LCP(L,R)開始比對，節省一點時間。然而時間複雜度仍是O(PlogT)。

P與L R經常有共同前綴。P與M比大小之前，可以預先計算LCP(M,L)、LCP(M,R)，如果小於LCP(P,L)、LCP(P,R)，就毋需比對。看誰長得像，直接得到M'。時間複雜度降為O(P+logT)。

預先建立LCP Array與「偽線段樹」，從LCP Array查詢區間最小值，得以迅速求得LCP。

一、P與M的共同前綴，往後不必再比對，O(P)。二、查詢區間最小值，區間逐次減半，O(logT + logT/2 + logT/4 + ... ) = O(logT)。三、總時間複雜度O(P+logT)。

【待補程式碼】

ICPC 4657

普通的建立方法

把一個字串的所有後綴，統統塞入一棵Trie。

時間複雜度O(T²)，空間複雜度O(T²A)。

運用suffix link的建立方法

先前介紹Aho–Corasick Algorithm曾經提過suffix link：每個節點各自牽一條線到次長後綴所在節點。

運用suffix link，就能online建立Suffix Trie，而且不必重覆遍歷已經建立的節點。每加入一個字元，就從最深的節點開始走訪suffix link、建立新節點。

加入所有字元之後，記得標出每個後綴所在節點。

時間複雜度仍是O(T²)，空間複雜度仍是O(T²A)。

char s[10000 + 1]; struct Node { bool word; Node* l[128], *suffix; Node() { word = false; suffix = 0; memset(l, 0, sizeof(l)); } }; void suffix_trie() { Node* root = new Node(), *deepest = root; for (int i=0; s[i]; ++i) // 逐次加入字元s[i]。 { // 從最深的節點開始走訪suffix link Node* prev_q = 0; for (Node* p = deepest; true; p = p->suffix) { Node* q = p->l[s[i]]; if (!q) // 節點尚未建立 { p->l[s[i]] = q = new Node(); if (prev_q) prev_q->suffix = q; prev_q = q; } else // 節點已經建立 { if (prev_q) prev_q->suffix = q; break; } } deepest = deepest->l[s[i]]; } // 標出每個後綴所在節點 for (Node* p = deepest; p; p = p->suffix) p->word = true; }

字串搜尋

從T找到一個P：從樹根開始走訪Suffix Trie，看看有沒有P。時間複雜度O(P)。

從T找到全部P：建立Suffix Trie的時候，每個節點都必須額外記錄有哪些後綴經過。

Suffix Tree

「後綴樹」是Suffix Trie的改良版本：

一、字串結尾添加一個從未出現的字元（例如'\0'），再來建立Suffix Trie。如此一來，後綴結尾總是出現在樹葉，不會出現在內部節點，就不必特別記錄後綴所在節點。

二、去除沒有分叉的節點，一串樹枝合併成一根樹枝。

三、樹枝上的子字串，改為兩個索引值、或者兩個指標。

後綴樹共T+1個樹葉。字元皆相同，節點最多，共2T+1個節點；字元皆不同，節點最少，共T+2個節點。空間複雜度O(TA)。

演算法（Ukkonen's Algorithm）

運用suffix link，是online演算法，時間複雜度O(T+A)。

樹葉終身是樹葉。每次加入一個字元、要建立新節點時，不必回到最深的節點，可以從當前的節點繼續。

char s[10000 + 1]; // 該節點上方的樹枝，儲存s[a,b)的字元。 struct Node { int a, b; Node* l[128], *suffix; Node(int a, int b): a(a), b(b), suffix(0) { memset(l, 0, sizeof(l)); } }; void Ukkonen() { Node* root = new Node(0, 0), *p = root; // 逐次加入字元s[i]。包含'\0'。 int N = strlen(s); for (int a=0, i=0; i<N+1; ++i) { Node* ant = root; while (a <= i) { // 往下走，直到字元s[i-1]出現。 while (true) { if (a == i) break; Node* q = p->l[s[a]]; if (a + q->b - q->a > i) break; a += q->b - q->a; p = q; } Node* q = p; if (a == i) // s[i-1]位在樹枝末梢。 { // 節點已經建立。 if (p->l[s[i]]) break; } else if (a < i) // s[i-1]位在樹枝中間。 { // 節點已經建立。 Node* r = p->l[s[a]]; int k = r->a + i - a; if (s[i] == s[k]) break; // 節點尚未建立。 // 分裂此樹枝，以利將來插入樹葉。 p->l[s[a]] = q = new Node(r->a, k); q->l[s[k]] = r; r->a = k; } // 建立樹葉。終身為葉。 q->l[s[i]] = new Node(i, 1e9); // 建立上次樹葉的suffix link，連到這次樹葉。 // 至於這次樹葉的suffix link要等到下次才知道。 if (ant != root) ant->suffix = q; ant = q; // 走訪suffix link if (p->suffix) p = p->suffix; else a++; // 次長後綴在同一個節點 } if (ant != root) ant->suffix = p; } }

演算法（Farach's Algorithm）

時間複雜度O(T)。時間複雜度不含字元數量，但是不實用，參考看看就好。

字串搜尋

從T找到一個P：從樹根開始走訪後綴樹，看看有沒有P。時間複雜度O(P)。

從T找到全部P：從後綴樹找到P之後，遍歷子樹。P在T當中的出現次數，就是子樹的葉子數量。P在T當中的出現位置，就是 [ T長度 - 葉子深度 , T長度 - 葉子深度 + 當前節點深度 ]。

後綴樹是二元樹，內部節點數量等於葉子數量減一。因此子樹最多2K-1個節點，K是出現次數。時間複雜度O(P+K)。

Suffix Tray

Suffix Tree和Suffix Array一併使用。

Suffix Automaton

「後綴自動機」。把後綴通通塞入一個自動機。