rooted tree
rooted tree
「有根樹」。一棵樹,選定一個根。
有根樹可以重新繪製,讓所有邊朝著同一個方向延伸拓展,讓所有點有著先後次序。
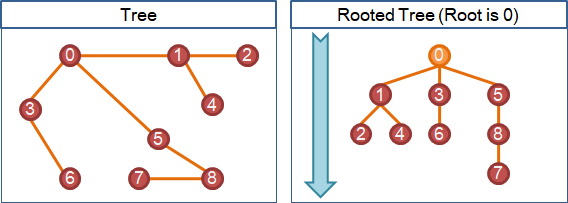
有根樹衍生許多概念:根、葉、父親、小孩、祖先、子孫、層、深度、高度。
rooted tree
rooted tree
「有根樹」。一棵樹,選定一個根。
有根樹可以重新繪製,讓所有邊朝著同一個方向延伸拓展,讓所有點有著先後次序。

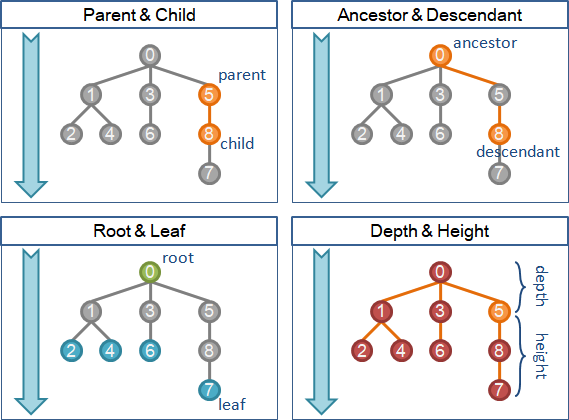
有根樹衍生許多概念:根、葉、父親、小孩、祖先、子孫、層、深度、高度。

ancestor
ancestor
「祖先」。有根樹,往根走,途中皆祖先。
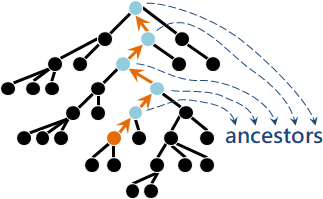
演算法(preprocessing)
利用DFS的遍歷順序,快速判斷一點是不是另一點的祖先。
建立O(V),查詢O(1)。(資料結構是adjacency lists。)
kth ancestor
kth ancestor
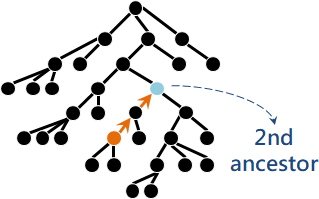
「第k祖先」。往根走k步。深度減少了k的祖先。
方便起見,如果輩分超過根,那麼祖先就是根。
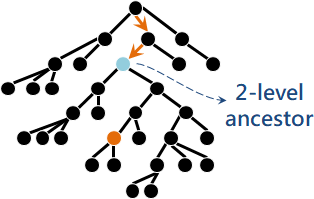
k-level ancestor
「第k層祖先」。從根走k步。深度為k的祖先。
方便起見,如果深度超過自己,那麼祖先就是自己。
演算法(preprocessing)
建立表格,紀錄每一點的祖先。很容易想到兩種策略:
一、每個點作為起點,實施遍歷,找到所有子孫。
二、每個點作為起點,走向樹根,找到所有祖先。
建立O(V²),查詢O(1)。
演算法(jump pointer algorithm)(binary lifting)
預先算好每個節點的上一輩祖先、上兩輩祖先、上四輩祖先、上八輩祖先、……。
k拆解成2的各種次方相加,分別對應2的各種次方輩祖先,合起來就是正確答案。
換句話說,k視作二進位數字,拆解成各種位數,分別對應各種2的各種次方輩祖先,合起來就是正確答案。
建立O(VlogV),查詢O(logV)。
演算法(deep path decomposition)
jump pointer algorithm:預先算好樹上每一點的上一輩祖先、上兩輩祖先、上四輩祖先、上八輩祖先、……。
deep path decomposition:一棵樹分解為數條不重疊長鏈。從樹根走到最深的樹葉,形成一條長鏈;然後遞迴分解其餘子樹。
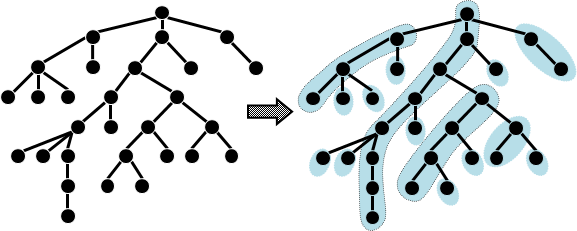
預先算好樹上每一點隸屬於哪一條長鏈。
一條長鏈,預先算好長度,往樹根方向延伸,讓長度翻倍,形成一把梯子。
一把梯子當中,預先算好梯子端點到其他點的距離,預先算好每一種距離隸屬於哪一點。如此便可迅速得到任意點的任意輩祖先。
令2ⁿ恰等於k、或略小於k。把k分成2ⁿ和(k-2ⁿ)兩部分。上2ⁿ輩祖先、再上(k-2ⁿ)輩祖先,合起來就是正確答案。
上2ⁿ輩祖先所屬長鏈,梯子長度充足,含有上(k-2ⁿ)輩祖先。
建立O(VlogV),查詢O(1)。
演算法(heavy path decomposition)
請見本站文件「heavy path decomposition」。
預先算好每一條長鏈的長度、端點到各點距離。最多遭遇logV條長鏈。
建立O(V),查詢O(logV)。
演算法(Euler tour technique)
請見本站文件「Euler tour technique」。
利用Euler tour technique將kth ancestor問題轉換成nearest smaller value問題。
建立O(VlogV),查詢O(logV)。
演算法(euler tour technique)
利用Euler tour technique將kth ancestor問題轉換成±1 nearest smaller value問題。
僅有理論上的價值,沒有實務上的價值。
建立O(VlogV),查詢O(1)。
lowest common ancestor
lowest common ancestor
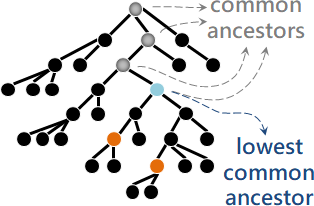
「最低共同祖先」。距離最近的共同祖先。深度最大的共同祖先。以下簡稱LCA。
方便起見,自己可以是自己的祖先。
演算法(Tarjan's algorithm)
建立表格,紀錄所有點對的LCA。
運用DFS遍歷順序,配合disjoint-sets forest,把已經拜訪過的點,依照層級合併,方便找到LCA。
建立O(V²),查詢O(1)。
亦得改成紀錄部分點對的LCA。必須預先知道是哪些點對,排好順序,以利實作。
建立O(V+Q),查詢O(1)。Q是點對數量。

UVa 12238 ICPC 2045
演算法(jump pointer algorithm)(binary lifting)
預先算好每個節點的上一輩祖先、上兩輩祖先、上四輩祖先、上八輩祖先、……,再以二元搜尋找到LCA。
建立O(VlogV),查詢O(logV)。
ICPC 5061
演算法(heavy path decomposition)
請見本站文件「heavy path decomposition」。
最多遭遇2logV條長鏈。
建立O(V),查詢O(logV)。
演算法(Euler tour technique)
請見本站文件「Euler tour technique」。
利用Euler tour technique將LCA問題轉換成RMQ問題。
建立O(V),查詢O(logV)。
演算法(Euler tour technique)
利用Euler tour technique將LCA問題轉換成±1RMQ問題。
僅有理論上的價值,沒有實務上的價值。
建立O(V),查詢O(1)。
directed acyclic graph
directed acyclic graph(DAG)
「有向無環圖」。有向圖,邊的走向一致,不會回頭。
DAG天生擁有起點與終點,稱作源與匯,宛如根與葉。
DAG可以重新繪製,讓所有邊朝著同一個方向延伸拓展,讓所有點有著先後次序。
depth
DAG可以仿照rooted tree定義「深度」。
一個點的「深度」,就是起點到該點的最遠距離。
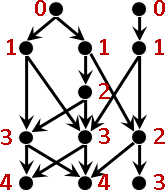
DAG有許多個起點。DAG有許多條路線抵達該點。邊數最多的路線,其邊數就是「深度」。
利用拓樸順序、取最大值,可求得各點的深度。
height
DAG可以仿照tree來定義「高度」。
一個點的「高度」,就是該點到終點的最遠距離。
lowest common ancestor
lowest common ancestor
DAG可以仿照rooted tree定義「最低共同祖先」。
兩個點的「最低共同祖先」,就是深度最深的共同祖先。
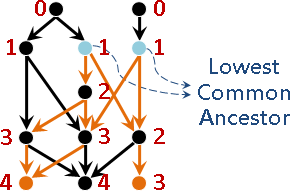
rooted tree只有唯一一個LCA。DAG可能有許多個LCA、也可能沒半個。
深度的定義
如果深度從最遠距離改成最近距離,會產生什麼問題呢?留給讀者想想看。
演算法
求出有向無環圖上所有點對的LCA。
一、每個點,求深度:拓樸順序、取最大值。 二、每個點,找出祖先們:每個點,作為起點,逆向graph traversal。 三、每個點對,找出LCA:窮舉共同祖先,深度最深的共同祖先就是LCA。
建立O(V³),查詢O(1)。
UVa 11457
演算法
建立O(VE),查詢O(1)。