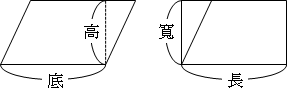simulation

撰寫程式，模擬行為。沒有前例，那就創例。

範例：印出直角三角形

不加思索，窮舉試誤。

// n 是三角形邊長 void print_triangle(int n) { // 依序窮舉每一個位置，逐一判斷要印什麼。 for (int i=0; i<n; i++) { for (int j=0; j<n; j++) { if (i + j < n - 1) cout << ' '; else cout << '@'; } cout << '\n'; } }

分割概念，編排步驟。

void print_triangle(int n) { // 直角三角形分成多行 for (int i=0; i<n; i++) { // 一行分成兩階段：空白、三角形 for (int j=0; j<n-i-1; j++) cout << ' '; for (int j=n-i-1; j<n; j++) cout << '@'; cout << '\n'; } }

抽取概念，變成函式。

// 一行：i 是行數、n 是三角形邊長 void print_line(int i, int n) { // 一行分成兩階段：空白、三角形 for (int j=0; j<n-i-1; j++) cout << ' '; for (int j=n-i-1; j<n; j++) cout << '@'; cout << '\n'; } void print_triangle(int n) { for (int i=0; i<n; i++) print_line(i, n); }

抽取差異，變成參數。

// 一串：n 是長度、c 是字元 void print_sequence(int n, char c) { for (int i=0; i<n; ++i) cout << c; } // 一行：i 是行數、n 是三角形邊長 void print_line(int i, int n) { print_sequence(n-i-1, ' '); print_sequence(i , '@'); cout << '\n'; } void print_triangle(int n) { for (int i=0; i<n; i++) print_line(i, n); }

對比排比，調整參數。

void print_sequence(int n, char c) { for (int i=0; i<n; ++i) cout << c; } // 一行：s 是空白長度、t 是符號長度（兩者都是填充長度） void print_line(int s, int t) { print_sequence(s, ' '); print_sequence(t, '@'); cout << '\n'; } void print_triangle(int n) { for (int i=0; i<n; i++) print_line(i, n-i-1); }

經過整頓，一目了然。容易閱讀，方便維護。

UVa 10550

範例：排隊上車

等車的人排成一列。人不時抵達，隊伍增長；車不時抵達，隊伍減短。請隨時記錄排隊隊伍依序是誰。

分割概念，編排步驟。

void lineup() { string array[100000]; int head = 0, tail = 0; string command; while (cin >> command) // 讀指令 { if (command == "people") // 先處理人 { string name; // 先讀指令 cin >> name; array[tail] = name; // 再做儲存 tail++; } else if (command == "car") // 再處理車 { int seat; // 先讀指令 cin >> seat; head += seat; // 再做儲存 } } }

抽取概念，變成函式。

string array[100000]; int head = 0, tail = 0; // 人來了 void people(string name) { array[tail] = name; tail++; } // 車來了 void car(int seat) { head += seat; } // 只讀指令 void lineup() { string command; while (cin >> command) if (command == "people") { string name; cin >> name; people(name); } else if (command == "car") { int seat; cin >> seat; car(seat); } }

對比排比，調整函式。

string array[100000]; int head = 0, tail = 0; // 人來了 void come(string name) { array[tail] = name; tail++; // 對比排比之後，事情變得單純，容易考慮的更細膩。 if (tail >= 100000) assert(false); } // 人走了 void leave() { // head++; // 對比排比之後，事情變得單純，容易考慮的更細膩。 if (head < tail) head++; } // 車來了 void car(int seat) { for (int i=0; i<seat; ++i) leave(); } void lineup() { string command; while (cin >> command) if (command == "people") { string name; cin >> name; come(name); } else if (command == "car") { int seat; cin >> seat; car(seat); } }

連同資料，變成物件。

// 排隊人生 struct Line { string array[100000]; int head = 0, tail = 0; void come(string name); // 人來了 void leave(); // 人走了 void car(int seat); // 車來了 }; void Line::come(string name) { array[tail] = name; tail++; if (tail >= 100000) assert(false); } void Line::leave() { if (head < tail) head++; } void Line::car(int seat) { for (int i=0; i<seat; ++i) leave(); } void lineup() { Line line; while (cin >> command) if (command == "people") { string name; cin >> name; line.come(name); } else if (command == "car") { int seat; cin >> seat; line.car(seat); } }

聯想他物，發明模型。

struct MultipopQueue { string array[100000]; int head = 0, tail = 0; void push(string name); // 原本是人來了 void pop(); // 原本是人走了 void multipop(int n); // 原本是車來了 }; template class<T> class MultipopQueue // 資料型別抽象化（從特例變通例） { private: T array[100000]; int head, tail; public: MultipopQueue(): head(0), tail(0) {} void push(const T& name); // 用特殊語法，做補充說明 void pop(); void multipop(const int n); // 用特殊語法，做補充說明 };

UVa 10267 476 477 478

範例：轉骰子

請辨別兩顆骰子一不一樣。骰子經過旋轉後，如果六個對應的面，上面的點數皆相同，則骰子視為相同。

要辨別兩顆骰子一不一樣，一種方式是旋轉其中一顆骰子，再跟另一顆比對。必須將骰子所有可能的情形都轉出來才行。

骰子有六個面：上下前後左右。建立六個變數、或者六格的陣列，分別儲存六個面的點數。陣列的第0格存入上面的點數、第1格存左面的點數、……。當然也可以採用不同的儲存方法。

骰子有三種旋轉方向：東西方向、南北方向、時鐘方向。我個人偏好的轉法是：東西方向轉一圈，順時針方向轉一圈，南北方向轉一下，以上動作循環四次，就能轉出所有情形。

亦得採用其他轉法，最好的轉法只需轉24次，讀者可以想想看怎麼做。

亦得預先計算所有旋轉結果，儲存於lookup table，以節省旋轉時間。

// 往西轉一下 void turn_west(int dice[6]) { int temp = dice[1]; dice[1] = dice[2]; dice[2] = dice[3]; dice[3] = dice[4]; dice[4] = temp; } // 六個面是否一一對應 bool equal(int a[6], int b[6]) { for (int i=0; i<6; i++) if (a[i] != b[i]) return false; return true; } // 兩顆骰子是否相同 bool check(int a[6], int b[6]) { for (int i=0; i<4; i++) { for (int j=0; j<4; j++) { turn_west(b); if (equal(a,b)) return true; } for (int j=0; j<4; j++) { turn_clockwise(b); if (equal(a,b)) return true; } turn_north(b); if (equal(a,b)) return true; } return false; }

UVa 253 10877

範例：踩地雷

試著用程式模擬踩地雷吧！

UVa 10189 10279 11142 ICPC 4335

範例：撲克牌

試著用程式模擬各種撲克牌遊戲吧！

UVa 127 131 162 170 178 181 451 462 555

範例：下棋

試著用程式模擬各種棋吧！

UVa 220 852 10196 10363 10996 11210 1589

範例：試算表

試著用程式模擬試算表吧！

UVa 196 215 512

modeling

把問題對應到耳熟能詳的模型，套用既有模型解決新問題。

範例：平行四邊形面積

小學數學老師教過：長方形的面積是「長乘寬」。儘管不知道原因，不過這個公式肯定是正確的。那麼，請問平行四邊形面積如何計算？

把平行四邊形凸出的三角形切下來，補在另一邊，平行四邊形就變成了長方形。想要計算平行四邊形面積，可以直接套用長方形面積公式。

平行四邊形的底，就是長方形的長；平行四邊形的高，就是長方形的寬。平行四邊形的元件，一一對應到長方形。

範例：約瑟夫問題（Josephus problem）

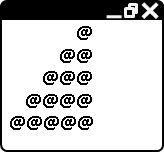
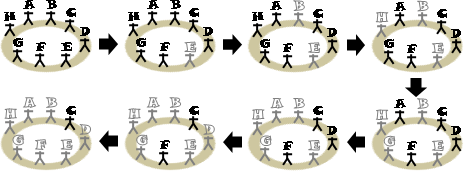
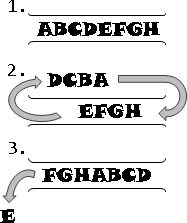
8個人圍成一圈，現在從第一個人開始報數，數到第5人時，就殺死這第5人；然後從被殺的下一位繼續重新報數，數到第5人時，就殺死這第5人。如此不斷數5人、殺此人，直到最後會剩下一個人，請問他是誰？

數人和殺人的動作可以對應到佇列（queue）的操作。首先把每個人依序塞入佇列，接著連續pop和push 4人，接著pop第5人時，不要將他塞回佇列裡面即可！

範例：用圖論作為模型，模擬小畫家倒墨水。

以圖論的觀點來看，flood fill algorithm其實就是運用depth-first search找到connected component。

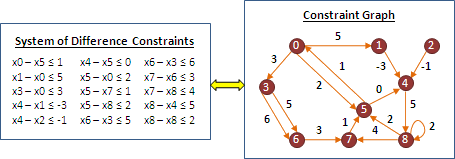
範例：system of difference constraints in linear programming

問題：給定變數x₁到xɴ，並給定一些xᵢ-xⱼ≤c的式子，作為條件限制。請判斷有沒有解，如果有解就求出其中一組解。

這個問題可以巧妙的轉換成最短路徑問題。x₁到xɴ看作是圖上的N個點，一道xᵢ-xⱼ≤c的限制式子看作是一條xⱼ到xᵢ的邊，其權重是c。

如果無解，那麼圖上有負環。如果有解，那麼圖上各點的最短路徑長度就是其中一組解。為了讓圖上各點都有最短路徑長度值，可參考Johnson's algorithm的做法。

UVa 515 ICPC 2058

範例：sentiment relation in social balance theory

從前有一位心理學者認為，人與人之間的關係，可以粗略分為兩種：互相喜歡、互相討厭。這種關係稱作sentiment relation，是一種雙向關係，而且擁有喜歡與討厭兩種類型。假使兩人之間好惡分明，沒有亦敵亦友的情況，就會形成sentiment relation。

   like            hate
A<------>B      A<------>B

另外sentiment relation還具有相當特殊的性質，有點像是transitivity、symmetry、antisymmetry的總合。這種性質的最佳寫照，諸如同仇敵愾、合縱連橫等等，翻成白話就是這樣：

1. 朋友的朋友就是我的朋友。
2. 朋友的敵人就是我的敵人。
3. 敵人的朋友就是我的敵人。
4. 敵人的敵人就是我的朋友。

在sentiment relation所形成的社交結構當中，如果產生了好與惡的矛盾，那麼這樣的社交結構就是不平衡的；如果好與惡合理，那麼這樣的社交結構就是平衡的。心理學者相信，當社交結構不平衡的時候，個體會嘗試改變自己的觀點，讓社交結構趨向平衡。

balance:

      A                A           like   like
like / \ like    hate / \ hate      ----A----
    /   \            /   \         /  ha|te  \
   B-----C          B-----C       B-----C-----D
     like             like         hate   hate
 
imbalance:

      A                A           like   like
hate / \ hate    like / \ like      ----A----
    /   \            /   \         /  ha|te  \
   B-----C          B-----C       B-----C-----D
     hate             hate         like   like

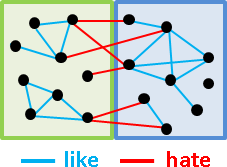
後來心理學者進一步發現，當社交結構達到平衡，所有人可以分成兩大陣營，使得陣營內部的關係都是互相喜歡，陣營與陣營之間的關係都是互相討厭。

說了這麼多終於要提到重點。現在問題來了，假設社交結構是平衡的，而我們也知道一些兩兩相互喜歡、相互討厭的資訊時，我們該如何確認誰在同一陣營、誰在不同陣營呢？

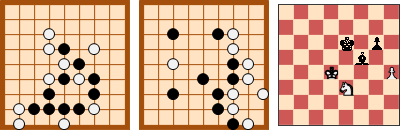
一、以bipartite graph作為模型：

把社交結構看作是bipartite graph，bipartite graph的兩側分別是兩大陣營。首先利用graph traversal走訪喜歡的邊，找出所有連通分量，並各自縮成一點。然後再度利用graph traversal走訪討厭的邊，嘗試建立bipartite graph，如果無法建立則表示社交結構不平衡。

二、以disjoint sets作為模型：

當x與y是朋友：
　x及朋友、y及朋友，都是好朋友。
　x的敵人、y的敵人，都是好朋友。

當x與y是敵人：
　x及朋友、y的敵人，都是好朋友。
　x的敵人、y及朋友，都是好朋友。

把陣營看作是disjoint sets，利用merge把好朋友們聯集在一起。要判斷同一陣營，就看看大家是不是同一群好朋友；要判斷不同陣營，就看看對方的敵人是不是跟自己是同一群好朋友。由於一開始每個人都沒有敵人，所以替每個人都設定一個虛擬的假想敵。

#define _x (x + 100) // x的假想敵 #define _y (y + 100) // y的假想敵 // disjoint-sets forest int p[100 + 100]; // 前百人為本尊，後百人為假想敵。 void init() {for (int i=0; i<200; ++i) p[i] = i;} int find(int x) {return x == p[x] ? x : (p[x] = find(p[x]));} void merge(int x, int y) {p[find(x)] = find(y);} bool if_like(int x, int y) { return find(x) == find(y); // return find(_x) == find(_y); } bool if_hate(int x, int y) { return find(x) == find(_y); // return find(_x) == find(y); } // 結交朋友 void like(int x, int y) { if (if_hate(x, y)) return; // imbalance merge(x, y); merge(_x, _y); } // 樹立敵人 void hate(int x, int y) { if (if_like(x, y)) return; // imbalance merge(x, _y); merge(_x, y); }

UVa 10158 10505 10608

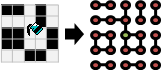
範例：點燈遊戲（lights out puzzle）（minimum all-ones problem）

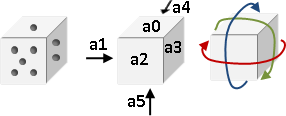
嘗試熄滅（或點燃）所有燈。按下任何一個開關，都會連帶影響自己及其四周的燈，亮變暗、暗變亮。

無論同時按或分開按、先按或後按，造成的影響都一樣。一個開關按兩次，將相互抵銷，如同按零次。

一、以函數當作模型，函數是各盤面之間的關聯：g(舊盤面) = 新盤面，g為一種按開關的方式。這種模型相當常見，但是不適用此題。

二、以函數當作模型，函數是開關和盤面的對應關係：f(按下的開關) = 盤面，f是遊戲規則。

只要求出f的反函數，就可以用盤面判斷按下的開關。巧妙的是，f是線性函數，故可以解一次方程組來找到反函數。解一次方程組可以用「高斯消去法」。

加法運算：f(同時按下開關A和B) = f(按下開關A) + f(按下開關B)。設定成xor。
倍率運算：f(按下開關A一共k次) = k f(按下開關A)。k模二之後，設定成and。

然而f不見得有反函數，端看遊戲規則和盤面形狀。當f有反函數，無論盤面長得如何，都一定有解。當f沒有反函數時，則難以確定盤面是否有解，屬於NP-complete問題。

UVa 10309 10318 ICPC 8045

reduction

套用模型當中，有一種情況是：原問題是某一個問題的特例。套用通例，解決特例，稱作「歸約」。

因為通例相對複雜、特例相對單純，所以原問題極可能存在更快更好的解法。

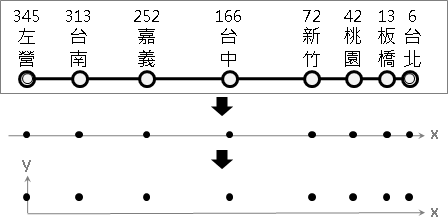
範例：最短間距（minimum gap problem）

一條鐵道，沿途設站。已知里程，請找出距離最近的兩站。

以數線作為模型，鐵道對應到數線、車站對應到點座標，距離最近的兩站對應到「數線上距離最近的兩個點」。

想要解決「數線上距離最近的兩個點」，可以套用先前介紹的「平面上距離最近的兩個點」。這兩個問題的本質是相同的，前者是一維版本，後者是二維版本；前者是特例，後者是通例。

只要把每個車站的座標，增加一個維度，該維度的數值通通設定為相同數值，然後計算「平面上距離最近的兩個點」，就得到距離最近的兩站。

「數線上距離最近的兩個點」是特例、「平面上距離最近的兩個點」是通例，我們有機會替「數線上距離最近的兩個點」找到計算時間更短、更有效率的演算法。

範例：用生命遊戲作為模型，模擬生命遊戲。