linear programming
mathematical programming
「數學規劃」即是約束最佳化。已經發展成一系列問題:
linear programming min cᵀx subject to Ax ≤ b quadratic programming min 1/2 xᵀQx + cᵀx subject to Ax ≤ b second order cone programming min fᵀx subject to ‖Aᵢx + bᵢ‖ ≤ cᵢᵀx + dᵢ, Fx = g semidefinite programming min C●X subject to Aᵢ●X ≤ bᵢ, X ≽ 0 min tr(CX) subject to tr(AᵢX) ≤ bᵢ, X ≽ 0
LP ⊂ QP ⊂ SOCP ⊂ SDP
現代社會經常使用數學規劃,例如經濟交易、交通運輸、工業生產。數學規劃儘管不是電資科系的學習重點,然而卻是商管科系的必修專業。
經典數學領域亦可使用數學規劃,例如組合最佳化。數學規劃比起經典組合算法,有過之而無不及,計算時間更短。
minimum ratio spanning tree: Dinkelbach's algorithm http://sunmoon-template.blogspot.com/2016/12/0-1-fractional-programming-dinkelbach.html
知名工具Gurobi、CPLEX、GAMS。大家把現實世界問題改寫成數學規劃問題,運用工具快速得到答案。
linear programming
「一次規劃」、「線性規劃」。一次函數的約束最佳化。目標函數、約束函數都是一次函數。
minimize x₁ + 2x₂ - x₃ + 1
subject to 3x₁ + 2x₂ + x₃ + 1 < 3
-4x₁ - 5x₂ + 6x₃ + 1 ≥ 4
7x₁ + 8x₂ - 9x₃ - 2 = 5
linear programming標準式
調整式子,美化式子。數學家的最愛。
maximize -x₁ - 2x₂ + x₃
subject to 3x₁ + 2x₂ + x₃ ≤ 2
4x₁ + 5x₂ - 6x₃ ≤ -3
7x₁ + 8x₂ - 9x₃ ≤ 7
-7x₁ - 8x₂ + 9x₃ ≤ -7
x₁, x₂, x₃ ≥ 0
步驟很簡單,只是有點多。
一、目標函數,一律移除常數。 二、目標函數,一律求最大值。(式子視情況乘上-1。) 三、約束條件,一律將常數移項至右側。 四、約束條件,一律包含等於。 五、約束條件,一律是不等式。(一道等式拆成兩道不等式。) 六、約束條件,一律是小於等於。(式子視情況乘上-1。) 七、約束條件,一律是非負變數。(一個無界變數拆成兩個非負變數相減。)
一、目標函數,一律移除常數。
minimize x₁ + 2x₂ - x₃
subject to 3x₁ + 2x₂ + x₃ + 1 < 3
-4x₁ - 5x₂ + 6x₃ + 1 ≥ 4
7x₁ + 8x₂ - 9x₃ - 2 = 5
二、目標函數,一律求最大值。(式子視情況乘上-1。)
maximize -x₁ - 2x₂ + x₃
subject to 3x₁ + 2x₂ + x₃ + 1 < 3
-4x₁ - 5x₂ + 6x₃ + 1 ≥ 4
7x₁ + 8x₂ - 9x₃ - 2 = 5
三、約束條件,一律將常數移項至右側。
maximize -x₁ - 2x₂ + x₃
subject to 3x₁ + 2x₂ + x₃ < 2
-4x₁ - 5x₂ + 6x₃ ≥ 3
7x₁ + 8x₂ - 9x₃ = 7
四、約束條件,一律包含等於。
maximize -x₁ - 2x₂ + x₃
subject to 3x₁ + 2x₂ + x₃ ≤ 2
-4x₁ - 5x₂ + 6x₃ ≥ 3
7x₁ + 8x₂ - 9x₃ = 7
五、約束條件,一律是不等式。(一道等式拆成兩道不等式。)
maximize -x₁ - 2x₂ + x₃
subject to 3x₁ + 2x₂ + x₃ ≤ 2
-4x₁ - 5x₂ + 6x₃ ≥ 3
7x₁ + 8x₂ - 9x₃ ≤ 7
7x₁ + 8x₂ - 9x₃ ≥ 7
六、約束條件,一律是小於等於。(式子視情況乘上-1。)
maximize -x₁ - 2x₂ + x₃
subject to 3x₁ + 2x₂ + x₃ ≤ 2
4x₁ + 5x₂ - 6x₃ ≤ -3
7x₁ + 8x₂ - 9x₃ ≤ 7
-7x₁ - 8x₂ + 9x₃ ≤ -7
七、約束條件,一律是非負變數。(一個無界變數拆成兩個非負變數相減。)
maximize -(x₁₊ - x₁₋) - 2(x₂₊ - x₂₋) + (x₃₊ - x₃₋)
subject to 3(x₁₊ - x₁₋) + 2(x₂₊ - x₂₋) + (x₃₊ - x₃₋) ≤ 2
4(x₁₊ - x₁₋) + 5(x₂₊ - x₂₋) - 6(x₃₊ - x₃₋) ≤ -3
7(x₁₊ - x₁₋) + 8(x₂₊ - x₂₋) - 9(x₃₊ - x₃₋) ≤ 7
-7(x₁₊ - x₁₋) - 8(x₂₊ - x₂₋) + 9(x₃₊ - x₃₋) ≤ -7
x₁₊, x₁₋, x₂₊, x₂₋, x₃₊, x₃₋ ≥ 0
實際應用當中,變數通常就是非負,或者最佳解位置通常就是非負。這種時候,直接追加非負條件,不影響答案。大可不必拆變數。
maximize -x₁ - 2x₂ + x₃
subject to 3x₁ + 2x₂ + x₃ ≤ 2
4x₁ + 5x₂ - 6x₃ ≤ -3
7x₁ + 8x₂ - 9x₃ ≤ 7
-7x₁ - 8x₂ + 9x₃ ≤ -7
x₁, x₂, x₃ ≥ 0
至此得到標準式。
linear programming矩陣運算形式
標準式可以寫成矩陣運算。
max cᵀx subject to Ax ≤ b, x ≥ 0
⎡ -1 ⎤ ⎡ x₁ ⎤ ⎡ 3 2 1 ⎤ ⎡ 2 ⎤
c = ⎢ -2 ⎥ x = ⎢ x₂ ⎥ A = ⎢ 4 5 -6 ⎥ b = ⎢ -3 ⎥
⎣ 1 ⎦ ⎣ x₃ ⎦ ⎢ 7 8 -9 ⎥ ⎢ 7 ⎥
⎣ -7 -8 9 ⎦ ⎣ -7 ⎦
linear programming幾何意義
先備知識請見本站文件「half-plane」。
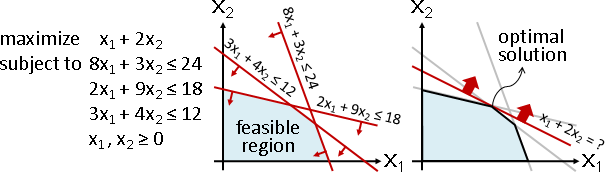
可行解:滿足約束條件的解。 最佳解:滿足約束條件與目標函數的解。
(以三維空間為例) 變數:座標軸。 目標函數:平面,朝著法向量移動。 約束函數:半空間。 可行解:半空間交集。 最佳解:半空間交集的邊界,可能包含點、邊、面。
「fundamental theorem of linear programming」:可行解形成凸多胞形。最佳解位於頂點,可能連成一片。
因此得以使用貪心法。隨便一個可行解,逐步修改可行解,朝著目標函數的方向走,維持在界內,必定可以走到其中一個最佳解。
「upper bound theorem for polytope」:N個變數(維度)、M道不等式(刻面),可行解至多C(M-⌈N/2⌉, ⌊N/2⌋) + C(M-⌊N/2⌋-1, ⌈N/2⌉-1)個頂點。
「d-Step conjecture」:N個變數(維度)、M道不等式(刻面),兩頂點的最短路徑至多M-N條邊。仍是懸案。
因此貪心法的時間複雜度仍是懸案。只知道至多是指數時間,不知道是否為多項式時間。
projective scaling algorithm(投影縮放法)
行走於可行解內部。理論上是多項式時間,實務上極慢。
請見專著《Operations Research: Applications and Algorithms》的Karmarkar's algorithm。
simplex algorithm(單形法)
行走於可行解的頂點與邊。理論上是指數時間,實務上極快。