Connected Graph

我可以往，彼可以來，曰通；通形者，先居高陽，利糧道以戰，則利。《孫子》

Connected

無向圖不必在意方向。兩點之間邊邊相連，就是「連通的」。

Connected Graph

「連通圖」。一張無向圖，所有兩點之間皆得以邊相通。

例如一棵樹就是一張連通圖。

運用Graph Traversal就能判斷連通圖。

Strongly Connected / Weakly Connected

有向圖必須考慮方向。兩點之間，雙向皆有路可通，就是「強連通的」。至少單向有路可通（可能雙向都通），就是「弱連通的」。

Strongly Connected Graph / Weakly Connected Graph

「強連通圖」。一張有向圖，所有兩點之間皆是強連通。

「弱連通圖」。一張有向圖，所有兩點之間皆是弱連通。

運用Graph Traversal就能判斷強連通圖、弱連通圖。

Articulation Vertex / Bridge

Articulation Vertex（Articulation Point）（Cut-vertex）

Articulation乃「關節」之意，骨骼與骨骼銜接的地方就是關節。關節一旦被拆開，肢體之間的連繫就被切斷了。

「關節點」。讓一張無向圖維持連通，不可或缺的點。只要從一張無向圖上移除了關節點（以及與之相連的邊），就會讓這張圖分離成更多部分，變得不連通。

Bridge（Cut-edge）

「橋」。只要從一張無向圖上移除了橋，就會讓這張圖分離成更多部分，變得不連通。

Articulation Vertex / Bridge: Tarjan's Algorithm

無向圖，尋找所有的Articulation Vertex

尋找所有關節點：逐一試驗圖上每一個點是不是關節點。

判斷一個點是不是關節點：從圖上移除此點，判斷圖是否連通。

判斷一張圖是不是連通圖：執行一次Graph Traversal。

這個演算法簡單易懂、容易實作，但是很花時間。

接下來介紹複雜難懂、不易實作，但是更快的演算法。

聯繫鄰居

移除一個點之後，此點的鄰居被隔開了。鄰居不能互相聯繫，則是關節點；鄰居能互相聯繫，則不是關節點。

原本路線＋替代路線＝環

移除一個點之後，經過此點的路線被截斷了。如果沒有替代路線，則是關節點。如果有替代路線，則不是關節點。

原本路線、替代路線，併在一起，如同一個環。如果沒有環，則是關節點。如果有環，則不是關節點。

利用DFS Tree

聯繫鄰居不太明確，替代路線不太明確，環就相當明確了。

沒有環，就是樹！把圖重新繪製成樹的模樣，就容易觀察環了。把圖重新繪製成樹的模樣，利用Graph Traversal就行了。這裡利用一下DFS Tree吧！

聯繫鄰居：如果「祖先與子樹」和「子樹與子樹」不能互相聯繫，則是關節點。

原本路線：tree edge。替代路線：back edge。

無向圖，尋找所有的Articulation Vertex

一、樹根：只需考慮「子樹與子樹」是否能互相聯繫。

DFS Tree當中，子樹之間沒有邊！「子樹與子樹」想要互相聯繫，只能經過樹根。

當樹根只有一棵子樹（一個小孩），則不是關節點。當樹根有兩棵以上的子樹（兩個以上的小孩），則是關節點。

二、其餘點：額外考慮「祖先與子樹」是否能互相聯繫。

祖先與每一棵子樹之間都有back edge，則不是關節點。祖先與其中一棵子樹之間缺少back edge，則是關節點。

時間複雜度是一次Graph Traversal的時間。圖的資料結構為Adjacency Matrix是O(V²)；圖的資料結構為Adjacency Lists是O(V+E)。

判斷祖先：運用DFS的遍歷時刻。

判斷祖先與子樹互相聯繫：建立一個陣列trace[]，紀錄自身與子孫們用back edge連到了哪個祖先。方便起見，紀錄最高祖先。

迴圈版本。multi-pass版本。

bool adj[9][9];	// adjacency matrix
int parent[9];	// 記錄DFS forest
int visit[9];	// 記錄每一點的DFS遍歷時刻，以判斷祖先與子孫。
int order[9];	// 記錄DFS遍歷順序
int trace[9];	// 記錄自身與子孫們用back edge連到的最高祖先
int ap[9];		// 記錄每一點是不是關節點

void articulation_vertex()
{
	/* DFS forest。計算visit、parent、order。 */

memset(visit, 0, sizeof(visit));
	int t = 0;	// 時刻

stack<int> stk;
	for (int r=0; r<9; ++r)
		if (!visit[r])
		{
			stk.push(r);
			parent[r] = r;

while (!stk.empty())
			{
				int i = stk.top(); stk.pop();
				if (visit[i]) continue;

visit[i] = t+1;
				order[t] = i;
				t++;

for (int j=0; j<9; ++j)
					if (adj[i][j] && !visit[j])
					{
						stk.push(j);
						parent[j] = i;
					}
			}
		}

/* 計算trace：自身與子孫們用back edge連到的最高祖先。 */

for (int t=9-1; t>=0; --t)	// DFS逆序，先算子孫才算祖先
	{
		int i = order[t];
		trace[i] = i;
		for (int j=0; j<9; ++j)
			if (adj[i][j])
				// tree edge
				if (visit[i] < visit[j] && i == parent[j])
				{
					if (visit[trace[j]] < visit[trace[i]])
						trace[i] = trace[j];
				}
				// back edge
				else if (visit[i] > visit[j] && parent[i] != j)
				{
					if (visit[j] < visit[trace[i]])
						trace[i] = j;
				}
	}

/* 計算ap：判斷關節點 */

for (int i=0; i<9; ++i)
		// 樹根
		if (i == parent[i])
		{
			int child = 0;
			for (int j=0; j<9; ++j)
				if (adj[i][j] && i != j && i == parent[j])
					child++;
			ap[i] = (child > 1);
		}
		// 其他節點
		else
		{
			ap[i] = false;
			for (int j=0; j<9; ++j)
				if (adj[i][j] && i == parent[j])
					if (visit[trace[j]] >= visit[i])
					{
						ap[i] = true;
						break;
					}
		}

for (int i=0; i<9; ++i)
		if (ap[i])
			cout << "第" << i << "點是關節點";
}

遞迴版本。one-pass版本。

bool adj[9][9];	// adjacency matrix
int visit[9];	// 記錄每一點的DFS遍歷時刻，以判斷祖先與子孫。
int trace[9];	// 記錄自身與子孫們用back edge連到的最高祖先
int t = 0;		// 時刻

void DFS(int p, int i)	// 第p點是第i點的父親
{
	visit[i] = ++t;		// 記錄遍歷時刻
	trace[i] = i;		// 最高祖先預設為自己
						// 尚未發現任何back edge
	int child = 0;		// 記錄第i點有幾個小孩
	bool ap = false;	// 記錄第i點是不是關節點

for (int j=0; j<9; ++j)			// 進行DFS
		if (adj[i][j] && j != p)	// 避免回頭路
			if (visit[j])			// back edge
			{
				// 記錄第i點自身用back edge連到的最高祖先
				if (visit[j] < visit[trace[i]])
					trace[i] = j;
			}
			else					// tree edge
			{
				child++;
				DFS(i, j);

// 記錄第i點的子孫們用back edge連到的最高祖先
				if (visit[trace[j]] < visit[trace[i]])
					trace[i] = trace[j];

// 第i點的祖先、第i點的其中一棵子樹（樹根為第j點）
				// 兩者之間缺少back edge，因此第i點為關節點。
				if (visit[trace[j]] >= visit[i])
					ap = true;
			}

// 判斷是不是關節點。樹根和非樹根分開判斷。
	if ((i == p && child > 1) || (i != p && ap))
		cout << "第" << i << "點是關節點";
}

void articulation_vertex()
{
	memset(visit, 0, sizeof(visit));
	t = 0;

for (int i=0; i<9; ++i)
		if (!visit[i])
			DFS(i, i);
}

UVa 315 10199

無向圖，尋找所有的Bridge

關節點：其中一棵子樹回不到祖先。

橋：子樹回不到祖先暨自身。

小心處理兩點之間有多條邊的情況。多重邊當中，有一條是tree edge，其餘都是back edge。

UVa 796 610 12783

奇技淫巧：編號改成時刻

讓程式碼再縮短一點點！

大家習慣將trace[]改成low[]。

trace[]存入點的編號，low[]改成存入點的遍歷時刻。

trace[]存入最高祖先，low[]改成存入最小遍歷時刻。

奇技淫巧：low[]修改定義

讓程式碼再縮短一點點！

原版：不斷往下走tree edge，最後走一次back edge，所能觸及的最高祖先。

新版：不斷往下走tree edge或往上走back edge，所能觸及的最高祖先。

修改定義之後，有兩處要跟著修改：

一、取最小值時，visit[j]換成low[j]。

二、針對當前點i，先走訪所有back edge，才走訪所有tree edge。如此最高祖先才會傳遞至子孫。

然而，傳遞任何一個祖先，就足以判斷關節點和橋。即便不調整走訪順序、即便最高祖先沒有傳遞至子孫、即便low[]不正確，依然足以判斷關節點和橋。程式碼無需修改。

關節點的程式碼，沒有太大變化。橋的程式碼，變得更短。

Dominator

一張有向圖，選定一個起點、一個終點。由起點到終點，途中的必經之點、沒有替代路線的點，稱作「支配點」；起點與終點本身也是支配點。途中的必經之邊，則尚未命名。

只要移除了支配點，起點到終點的連繫就被切斷了，呈現不連通的狀態。

想要判斷一個點不是支配點，只要從圖上移除此點，再看看起點到終點是否連通就好了。

支配點就像是交通要衝、軍事要津。守塔遊戲當中，最理想的禦敵之處，通常正是支配點：http://www.kingdomrush.com/。

Dominator Tree

最高支配點是起點，最低支配點是終點，次低支配點是離終點次近的支配點。

一張有向圖，選定一個起點，圖上各點分別作為終點，各個終點分別連向次低支配點，形成「支配樹」。只有唯一一種。

學過最短路徑的讀者，可以將支配樹類比為最短路徑樹。疊合所有支配點，成為支配樹；疊合所有最短路徑，成為最短路徑樹。支配點的支配點，也是支配點；最短路徑末端截去一段，也是最短路徑。

有向圖的關節點

有向圖的關節點，有兩種定義方式：移除關節點之後，不再強連通（雙通變單通、不通）、不再弱連通（有通變不通）。

尋找所有的強連通關節點：圖上任選一點，尋找此點出發的支配樹，以及尋找抵達此點的支配樹。這兩棵樹，除去樹根與樹葉之後所剩下的節點，取聯集，即是強連通關節點──但是不包含樹根。樹根必須另行判斷是否為強連通關節點。

尋找所有的弱連通關節點：改為取交集。

UVa 11902

Dominator: Lengauer–Tarjan Algorithm

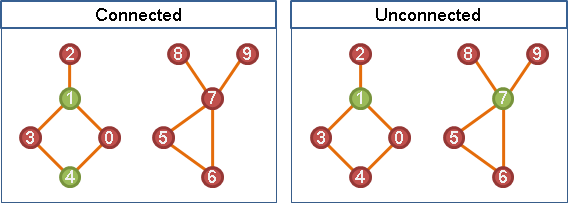
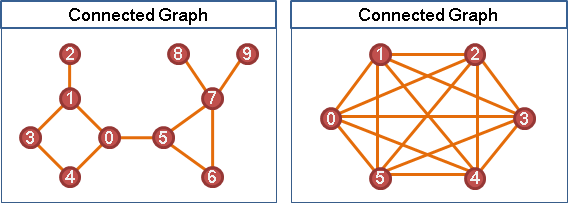
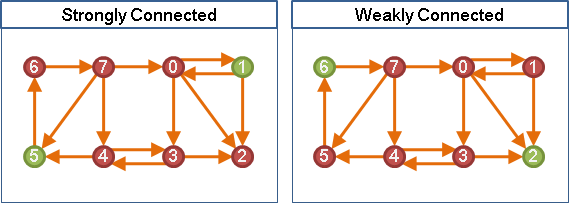
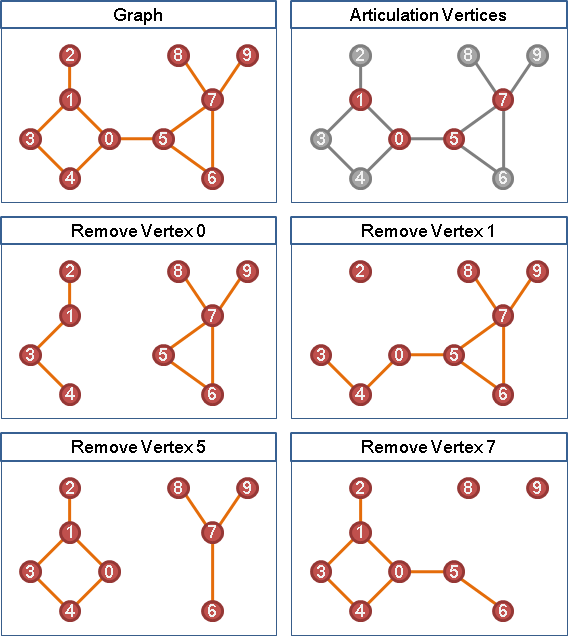
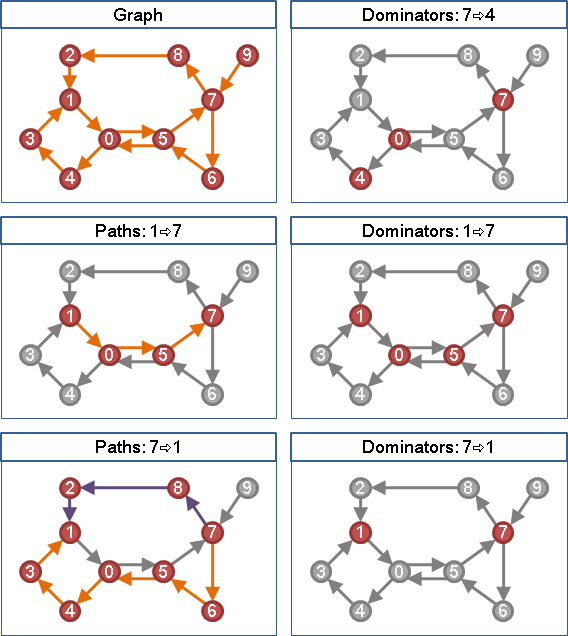
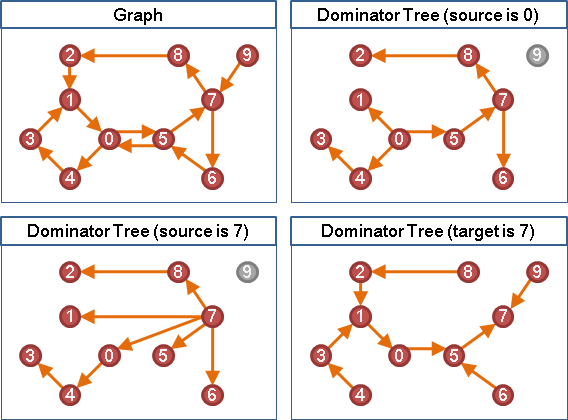
有向圖，給定起點，尋找所有的Dominator

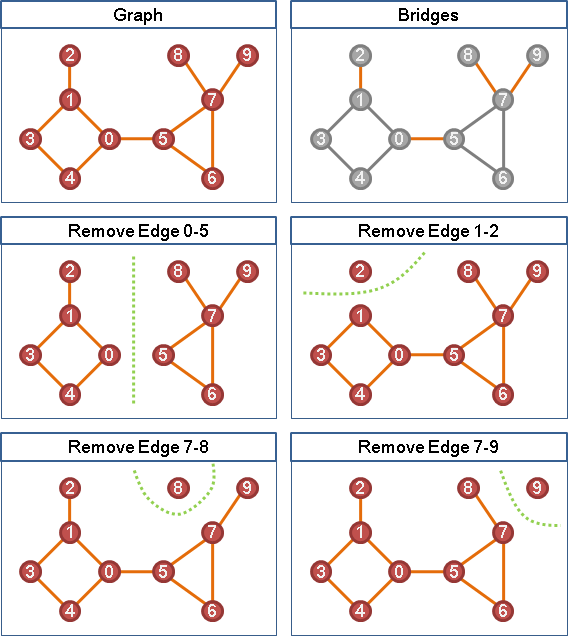
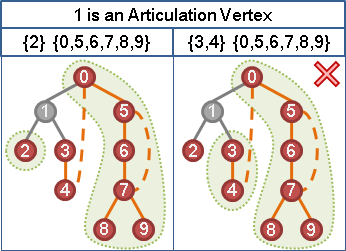
起點實施Graph Traversal。移除圖上一個點，再重新實施一次Graph Traversal。原先走得到、現在卻走不到的點，視作終點。移除的點，視作支配點。

輪流移除圖上每一個點，就能得到一種起點、每種終點的所有支配點。

這個演算法簡單易懂、容易實作，但是很花時間。

接下來介紹複雜難懂、不易實作，但是更快的演算法。

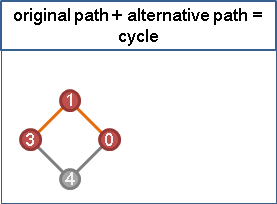
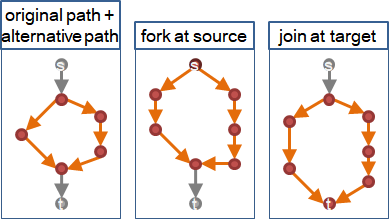
原本路線＋替代路線

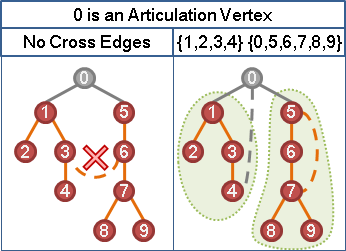
如果有替代路線，那麼「分岔點」到「會合點」之間的點，一定不是支配點！

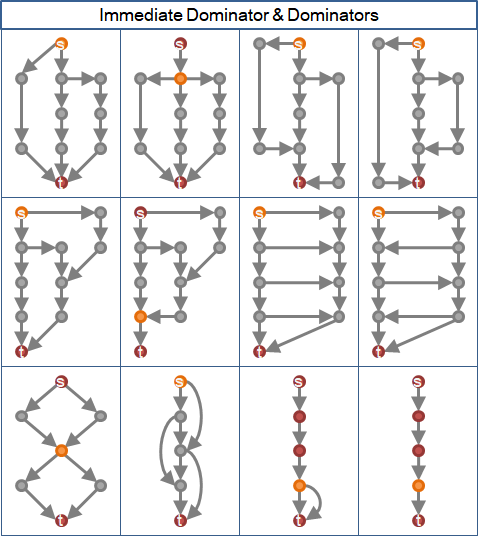
次低支配點【原始論文稱作Immediate Dominator】

給定起點與終點，支配點可能有許多個。方便起見，起點與終點計入支配點。離終點次近的支配點，稱作「次低支配點」。

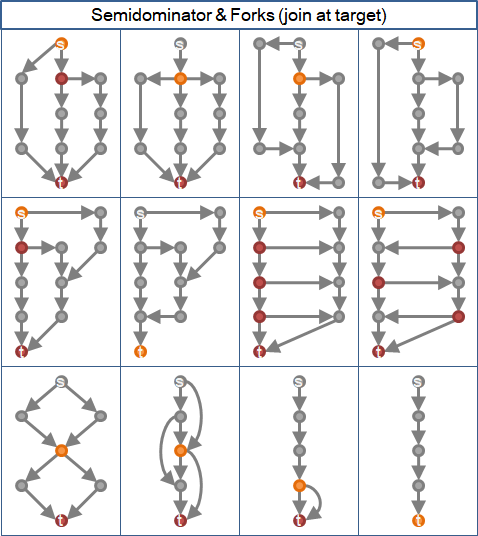
最高分岔點【原始論文稱作Semidominator】

給定起點與終點，分岔點可能有許多個。方便起見，終點計入分岔點。離起點最近的分岔點，稱作「最高分岔點」。

此處的最高分岔點，強制規定會合點是終點，方便使用遞歸法。

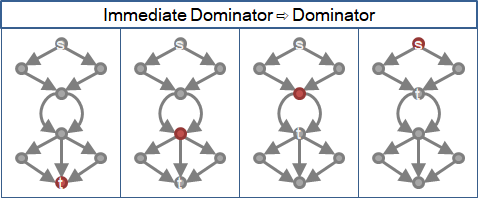
一、遞迴尋找次低支配點，得到所有支配點。

支配點的支配點，也是支配點。

次低支配點，作為新終點，再度尋找次低支配點。不斷遞迴，得到所有支配點。

二、遞迴尋找最高分岔點，得到次低支配點。

最高分岔點、次低支配點，不見得相同。尤其是麻花辮。

從最高分岔點到終點，途中的每個點，作為新終點，尋找最高分岔點。如果沒有變得更高，就不會形成麻花辮，次低支配點即是原本的最高分岔點。如果變得更高，就不斷遞迴，逼近次低支配點。

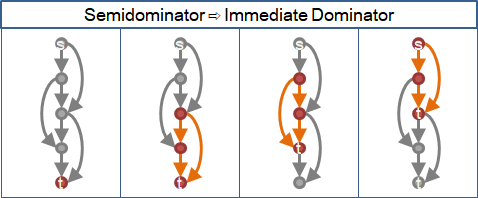
但是有一個例外：抵達終點的路線只有唯一一條，最高分岔點是終點，次低支配點是終點的父親。為了應付這個例外，最高分岔點必須強制改成終點的父親。

三、尋找後半段森林，得到最高分岔點。

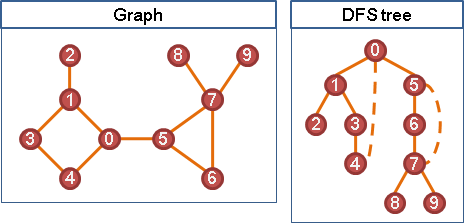
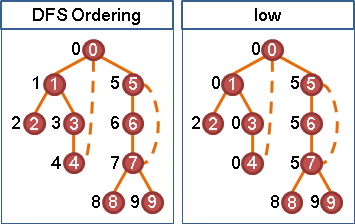
把圖重新繪製成樹的模樣，就容易觀察替代路線了。這裡利用一下DFS tree吧！

根據DFS Tree的性質，針對一個分岔點，原本路線只會經過樹上的邊，替代路線只會經過時刻更大的點。

原本路線與所有替代路線，時刻最小的點，就是該分岔點。

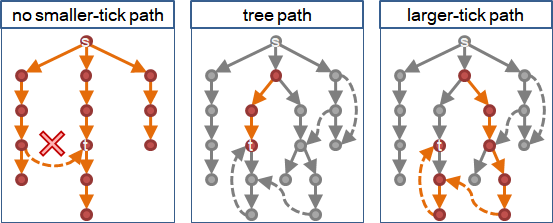
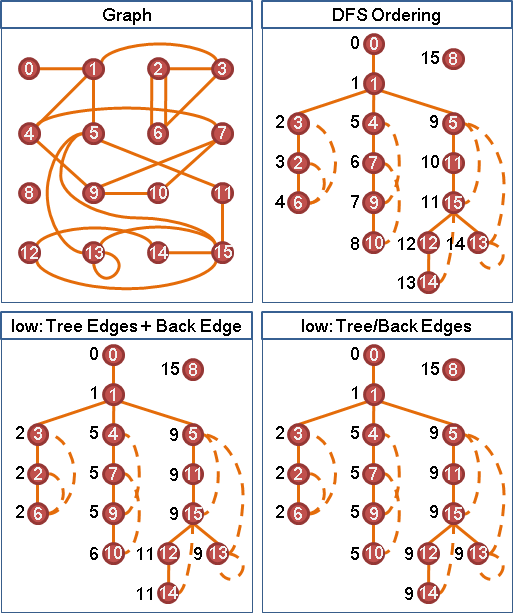
以分岔點為界，DFS tree後半段構成的森林（以及入邊），涵蓋了原本路線與所有替代路線。

以終點為界，DFS tree後半段構成的森林（以及入邊），涵蓋了所有替代路線。

針對一個終點，在森林（以及入邊）當中，抵達終點的所有路線，時刻最小的點，就是終點的最高分岔點。

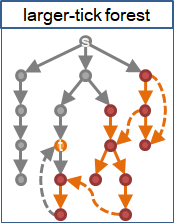
有向圖，給定起點，尋找每種終點的最高分岔點

計算順序定為「時刻從大到小」，讓後半段森林逐步成長。

時刻從大到小，依序作為終點，計算最高分岔點sdom[]。

針對一個終點，窮舉所有入邊，在後半段森林，找到最高分岔點sdom。

針對一條入邊，只需沿著tree edge逆行到森林頂端。這一條路線上的sdom，涵蓋了各種替代路線的最高分岔點。

窮舉所有入邊，也包括了父親，恰好能夠應付先前那個例外。

時間複雜度O(VE)。

bool adj[9][9];	// adjacency matrix
int parent[9];	// DFS tree
int visit[9];	// 記錄每一點的DFS遍歷時刻
int order[9];	// 記錄DFS遍歷順序
int t;			// 時刻
int p[9];		// DFS tree後半段構成的森林
int sdom[9];	// 最高分岔點

void DFS(int i)
{
	visit[i] = t;
	order[t] = i;
	t++;
	for (int j=0; j<9; ++j)
		if (adj[i][j] && visit[j] == -1)
		{
			parent[j] = i;
			DFS(j);
		}
}

// 沿著tree edge逆行到森林頂端，
// 求路線上sdom時刻最小值（位於哪個點）。
int find(int x)
{
	int best = x;
	for (x = p[x]; x != -1; x = p[x])
		if (visit[sdom[x]] < visit[sdom[best]])
			best = x;
	return best;
}

void semidominator(int r)
{
	// 建立DFS tree
	for (int i=0; i<9; ++i) visit[i] = -1;
	t = 0;
//	parent[r] = r;	// 不必做樹根
	DFS(r);

// 初始化
	for (int i=0; i<9; ++i) p[i] = -1;
	for (int i=0; i<9; ++i) sdom[i] = i;

// 時刻從大到小、從葉到根
	for (int k=t-1; k>0; --k)	// 不必做樹根order[0]
	{
		// 取出該時刻的節點
		int i = order[k];

// 抵達i點的所有路線：窮舉入邊，求路線上sdom時刻最小值。
		for (int j=0; j<9; ++j)
			if (adj[j][i] && visit[j] != -1)
			{
				// 路線sdom時刻最小值（位於哪個點）
				int best = find(j);
				if (visit[sdom[best]] < visit[sdom[i]])
					sdom[i] = sdom[best];
			}

// i點加入森林：窮舉出邊，讓i點小孩接上i點。
		for (int j=0; j<9; ++j)
			if (adj[i][j] && parent[j] == i)
				p[j] = i;
	}
}

奇技淫巧：Disjoint-sets Forest

後半段森林採用Disjoint-sets Forest。找到路線上的sdom時刻最小值之後，順手將路線上每一個點直接連向源頭，減少森林高度。恰巧不影響路線上sdom時刻最小值。

維護森林，本來是事後讓i點與小孩聯集，改成了事前讓i點與父親聯集！i點的sdom時刻最終將小於等於父親，而父親的sdom預設為自身，恰巧不影響sdom時刻最小值。

時間複雜度等同Graph Traversal的時間。圖的資料結構為Adjacency Matrix是O(V²)；圖的資料結構為Adjacency Lists是O(V+E)。

有向圖，給定起點，尋找每種終點的次低支配點（支配樹）
（Georgiadis–Tarjan–Werneck Algorithm）

時刻從小到大，遞迴尋找最高支配點，逼近次低支配點。

時間複雜度O(V²)。

有向圖，給定起點，尋找每種終點的次低支配點（支配樹）
（Lengauer–Tarjan Algorithm）

利用森林計算idom最小值。

時間複雜度等同Graph Traversal。但是速度比方才更慢。

原始論文宣稱O(ElogV)，畢竟那個時候還沒有均攤分析。

int idom[9];			// 次低支配點（支配樹）
vector<int> revsdom[9];	// 反向sdom

void dominator_tree(int r)
{
	for (int i=0; i<9; ++i) visit[i] = -1;
	t = 0;
//	parent[r] = r;
	DFS(r);

// 初始化
	for (int i=0; i<9; ++i)
	{
		p[i] = best[i] = sdom[i] = idom[i] = i;
//		revsdom[i].clear();
	}

for (int k=t-1; k>0; --k)
	{
		int i = order[k];
		for (int j=0; j<9; ++j)
			if (adj[j][i] && visit[j] != -1)
			{
				// 即時更新路線sdom最小值（位於哪個點）
				find(j);
				if (visit[sdom[best[j]]] < visit[sdom[i]])
					sdom[i] = sdom[best[j]];
			}

p[i] = parent[i];	// merge

// 記錄本次算得的sdom，方便找到對應。
		revsdom[sdom[i]].push_back(i);

// 利用森林計算idom最小值。
		// 從最高分岔點到終點，
		// 途中的每個點，作為新終點，尋找最高分岔點。
		// 暫時不遞迴。
		int x = parent[i];
		for (auto j: revsdom[x])
		{
			find(j);
			idom[j] = visit[sdom[best[j]]] < visit[x]
					? best[j] : x;
		}

// 清空已經處理過的路徑
		revsdom[x].clear();
	}

// 時刻從小到大，遞迴尋找最高支配點，逼近次低支配點。
	// 先前已經求得idom第一輪最小值。
	// 遞推法，前人種樹後人乘涼。
	// 只需做一步，無需迴圈。
//	idom[order[0]] = order[0];	// 樹根
	for (int k=1; k<t; ++k)
	{
		int i = order[k];
		if (idom[i] != sdom[i])
			idom[i] = idom[idom[i]];
	}
}

奇技淫巧：編號改成時刻

讓程式碼再縮短一點點！

sdom[]、idom[]、best[]，編號改成時刻。

Dominator: Cooper–Harvey–Kennedy Algorithm (Iterative Dominator Algorithm)

演算法

dom(s, t) = { dom(s, from1(t)) ∩ dom(s, from2(t)) ∩ ... } ∪ t

採用遞歸法，計算起點到終點的所有支配點：窮舉起點到終點的所有路線，計算起點到「終點的前一點」的所有支配點；各種路線的支配點們取交集，再補上終點。

以遞推方式，從起點開始，依序計算圖上各點的支配點。然而不幸的是：我們不明白計算順序！

當圖上無環，可以採用拓撲順序，只需遍歷一次。當圖上有環，只好採用偽拓樸順序：「DFS離開點的逆序」，反覆實施數次，趨近正確答案，直到答案不再變動，即是正確答案。

學過最短路徑的讀者，可以將此類比為「Label Correcting Algorithm」。重複遍歷的過程當中，儘管無法確定支配樹的長相，但是可以確定支配樹正在一層一層生長。

最多遍歷V次，每個點最多有V個「終點的前一點」，每一點最多有V個祖先、V個支配點，時間複雜度O(V³)。

如果只想求支配樹，按理應該可以改成計算起點到終點的次低支配點：窮舉起點到終點的所有路線，計算起點到「終點的前一點」的所有次低支配點的最低共同祖先LCA（取交集），再將終點連上LCA（補上終點）。

但是有向圖的LCA究竟如何定義高低呢？似乎還沒有人研究。