comparison

兩個元素互相「比較」。

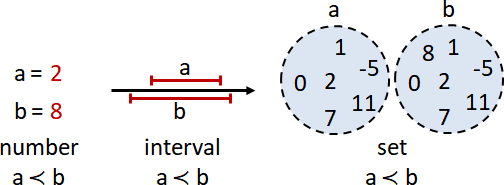
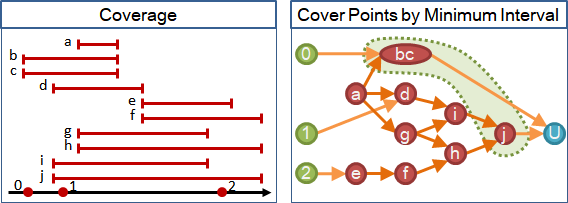
比較方式：高低（元素是數字）、覆蓋（元素是區間）、包含（元素是集合）、……。

比較結果：小於≺、等於∼、大於≻、無法比較。

比較結果可以精簡成兩種：小於等於≼、不小於等於⋠。

此處的數學符號是曲線！不是直線哦！

order

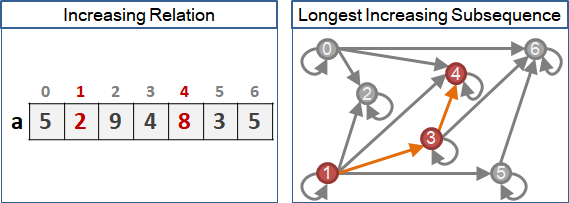
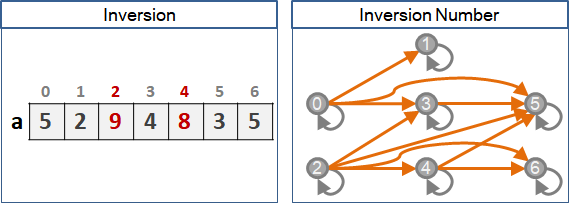
元素兩兩比較，宏觀望去，就是「序」。

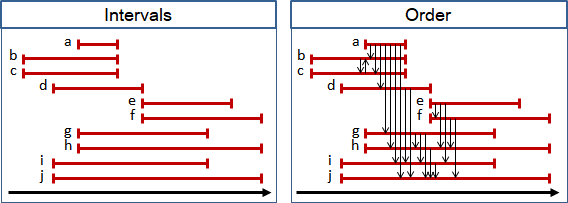
數學家習慣討論兩種特別的序：「偏序」和「全序」。

partial order

「偏序」在數學中擁有嚴謹定義。這些定義用來全面檢查元素大小，讓元素大小不產生矛盾：

1. a ≼ a                           (reflexivity)
   自反性：能夠自己跟自己比較
2. if a ≼ b and b ≼ a then a ∼ b   (antisymmetry)
   反對稱性：不大不小剛剛好
3. if a ≼ b and b ≼ c then a ≼ c   (transitivity)
   遞移性：一定要有直達捷徑

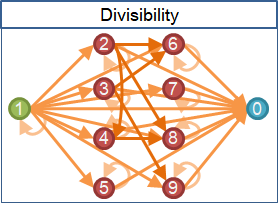
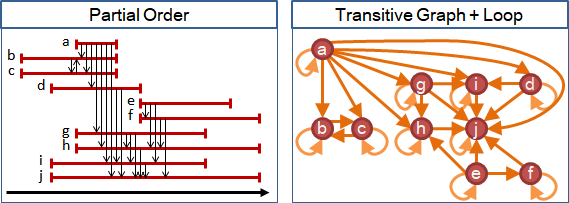
圖論的觀點，偏序是transitive graph添上loop。

相等元素之間形成一來一回兩條邊。相等元素們形成clique。

total order

「全序」是偏序的特例，追加第四點定義。

4. either a ≼ b or b ≼ a           (comparability)
   可比性：任意兩個元素一定能夠比較

圖論的觀點，全序是任意兩點之間，至少都有一條邊。

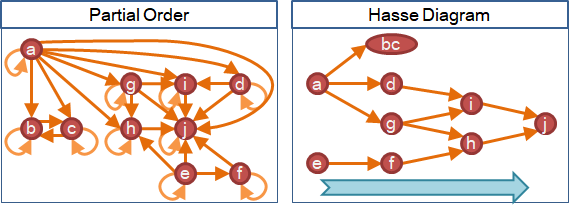
Hasse diagram

偏序和全序可以畫成簡圖，稱作「哈斯圖」。

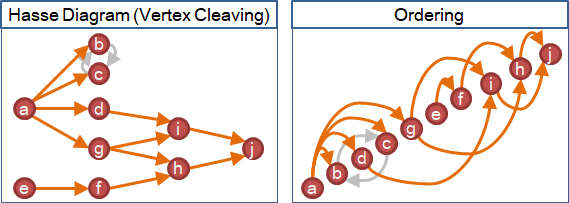
一、刪除自環：如果發現邊aa，就刪除邊aa。(reflexivity)
二、合併相等元素：如果發現邊ab、邊ba，就收縮邊ab。(antisymmetry)
三、刪除遞移：如果發現邊ab、邊bc、邊ac，就刪除邊ac。(transitivity)

圖論的觀點，哈斯圖是有向無環圖DAG。事先收縮所有clique，尋找minimum transitive reduction。

ordering

既然可以比較，那就可以分高下、定優劣、決勝負、論成敗。所有元素由小到大排成一列，形成「序列」。

order是兩兩關係，是一個graph。ordering是一條龍順序，是一個permutation。

order是限制條件。ordering是符合限制條件的排列。一個order通常可以擷取很多種ordering。

偏序　　　　　　　　丨全序
一一一一一一一一一一十一一一一一一一一一一一一一一一一一
部分配對可以互相比較丨所有配對皆可互相比較
哈斯圖是有向無環圖　丨哈斯圖是鏈
通常有許多種序列　　丨當元素皆不相等，只有唯一一種序列。

圖論的觀點，序列是拓樸順序topological ordering。事先清空所有clique的邊，實施拓樸排序。

圖論的觀點，序列也是哈斯圖的拓樸順序topological ordering。事先劈開所有收縮的點，實施拓樸排序。

partially ordered set（poset）

「偏序集」。所有集合元素形成偏序。

偏序集通常有許多種序列。

範例：divisibility

a ≼ b iff a | b

整除關係：元素是自然數。比較是整除。

從數字到數列，從數列到偏序集。數論進入了偏序集時代，重重謎團迎面而來。數字：群環體、複數運算。數列：多項式、級數運算。偏序集：我們所知甚少。

範例：domination

(x₁,y₁) ≼ (x₂,y₂) iff x₁ ≤ x₂ and y₁ ≤ y₂

支配關係：元素是座標。比較是對應維度座標大小。

經典問題：maximal layer。葉數。

範例：increasing relation

i₁ ≼ i₂ iff i₁ ≤ i₂ and a[i₁] ≤ a[i₂]

遞增關係：元素是數列的項。比較是項次先後、數字大小。

支配關係等價於遞增關係：X座標變項次、Y座標變數字。

經典問題：longest increasing subsequence。最長路徑。

範例：coverage

[a₁,b₁] ≼ [a₂,b₂] iff a₁ ≥ a₂ and b₁ ≤ b₂

覆蓋關係：元素是區間。比較是覆蓋。

支配關係等價於覆蓋關係：X座標變號。

經典問題：cover points by minimum interval。最小分隔集。

範例：inversion

i₁ ≼ i₂ iff i₁ ≤ i₂ and a[i₁] ≰ a[i₂]

逆序對關係：元素是數列的項。比較是項次先後、數字大小。

覆蓋關係等價於逆序對關係：左界變陣列數值、右界變索引值。

經典問題：inversion number。邊數（扣除自環）。

支配關係

方才四個經典問題都等價於支配關係。還有許多問題也都等價於支配關係，我就不一一介紹了。支配關係可以畫成有向無環圖DAG。這些問題的本質，就是針對DAG想空想縫、舞豬舞狗。

UVa 11020

totally ordered set

「全序集」。所有集合元素形成全序。

當全序集的元素皆不相等，則全序集只有唯一一種序列。

範例：natural number

自然數任意兩個數字皆可比較大小，而且數字皆不相等。

自然數、整數、有理數、代數數，乃至實數，其實都是全序集。

totally ordered set的各種運算

數學家不討論全序集的細節。計算學家恰恰相反，發明大量演算法，例如排序、搜尋、選擇、……，成為計算機科學的基本知識。

排序sorting：給定集合、序，求得序列。
索引indexing：給定集合、（序），求得索引集。
搜尋searching：給定索引集、（序）、元素，求得索引值。
排名ranking：給定集合、序、（元素），求得名次。
選擇selection：給定集合、序、名次，求得元素。

集合的每個元素予以編號，該集合稱作「索引集indexed set」，該編號稱作「索引值index」。若元素相同，則索引值相同。

集合的每個元素依「序」予以編號，該編號稱作「名次rank」。若元素相等，則名次相同。