◆想想看1：一組有2人，那麼該如何分組？
答：用之前所學的C來作分組的動作
先從6人中取2人出來為1組，
＝15種不同的分組組合
接下來再從4人中取2人出來再為新的1組，
＝6種不同的分組組合
最後一組也沒得選了，就剩２個人為一組，
＝１種不同的分組組合
◆想想看2：那麼總共有
這麼多種分組方式囉？
答：非也，非也。
◆想想看3：為何君云：「非也，非也。」難道事有蹊蹺？
答：假設有一種狀況......
（甲乙）在第一次選組時取出，
（丙丁）在第二次選組時取出，
（戊己）為剩下的２人為最後一組，此為平分成3組的一種狀況。
另外一種狀況......
（丙丁）在第一次選組時取出，
（戊己）在第二次選組時取出，
（甲乙）為剩下的２人為最後一組，此為平分成3組的另一種狀況。
不管這些組別到底在哪次選組時被取出，
結果都是這些人在同一組，理應視為同樣的分組方式。
所以，全部不同的分組方式應該有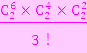
=10種
以後如果遇到分組呀,分隊呀,分堆等等情形
除了選出來之外，別忘了要把相同數量的組數排列情形除掉唷!
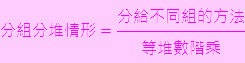
耶~想做練習題嗎@ˇ@?
可以去
小試身手
看看是不是都會了唷~!!!