舉一反三：
◆想想看1：若班際籃球賽要5人先發，本班有40人，
則有幾種先發名單組合？
答：位置1有40種選擇，位置2有39種選擇…
依此類推一共有40×39×38×37×36排列方式
但，甲乙丙丁戊 和 甲丙乙丁戊 等組合視為相同
所以，會有
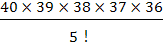種不同的先發名單組合。
◆想想看2：那麼，若一次立委選舉有n人參加，最後只選出m位為立法委員，
則有幾種不同的當選名單？
答：如法炮製，（n×(n-1)×(n-2)×…×(n-m+1)）÷（m！）這麼多種
一共有m項
每次都寫這麼多項，累不累啊？
累啊！有什麼方法可以不要寫得這麼累啊？
這種組合方式我們計作
，表示：有n種不同的東西，選ｍ個出來
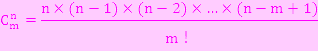
呀呼~答案就是這樣得出來的!
了解哩嗎~?
我們繼續下一個"不盡相異物的組合"囉^^