（一）三角函數的基本概念

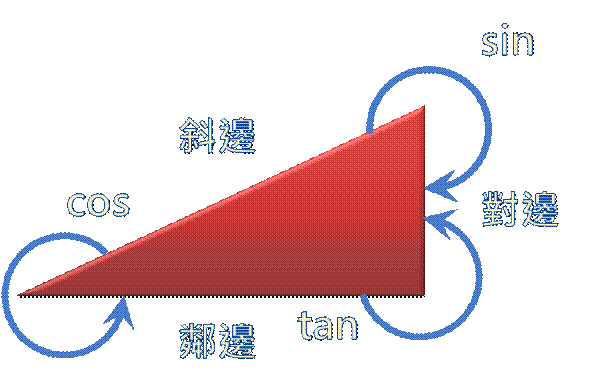
三角函數與三邊的關係 sin = 對邊/斜邊 cos = 鄰邊/斜邊 tan = 對邊/鄰邊 =sin/cos

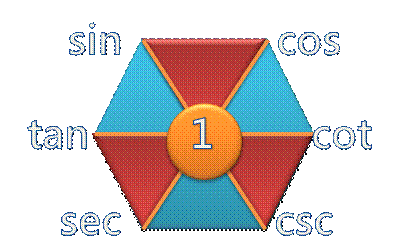
倒數(商數)關係 sin = 1/csc cos = 1/sec tan = 1/cot

平方關係 sin2+cos2 = 1 tan2+1 = sec2 1+cot2 = csc2

三角函數的值

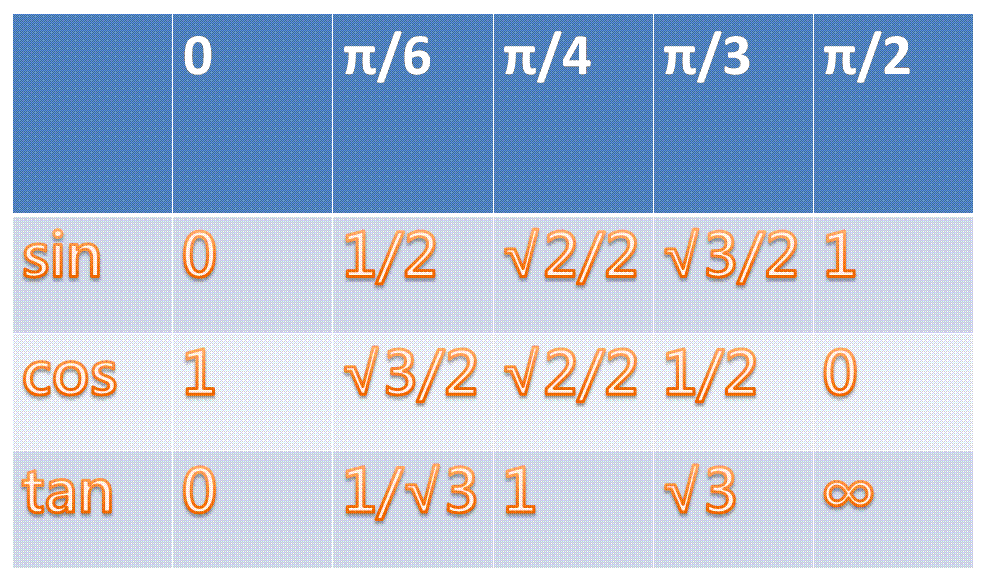
正弦定理

a/sinA = b/sinB = c/sinC = 2R

餘弦定理

cosA = (b²+c²-a²)/(2bc)
cosB = (a²+c²-b²)/(2ac)
cosC = (a²+b²-c²)/(2ab)

（二）三角函數的性質與運用
三角函數的圖形
正弦函數sine

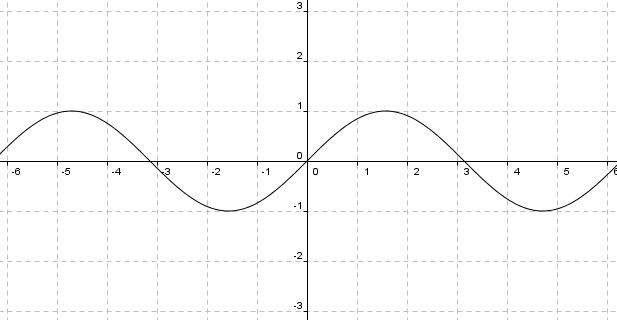
餘弦函數cosine

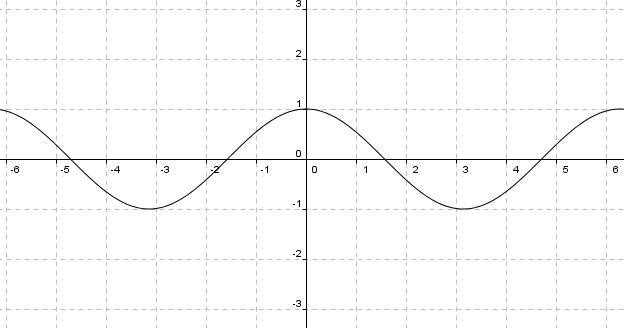
正切函數tangent

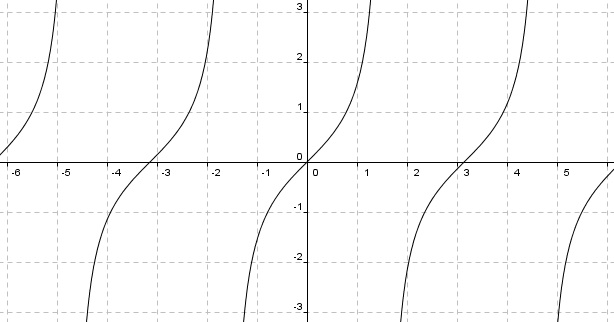
和角公式
sin(A+B) = sinAcosB+cosAsinB

sin(A-B) = sinAcosB-cosAsinB

cos(A+B) = cosAcosB-sinAsinB

cos(A-B) = cosAcosB+sinAsinB

倍角公式
sin2A = sin(A+A) = 2sinAcosA
sin3A = sin(2A+A) = 3sinA-4sin³A
cos2A = cos(A+A) = cos²A-sin²A = 1-2sin²A = 2cos²A-1
cos3A = cos(2A+A) = 4cos³A-3cosA

正餘弦函數之疊合
asinA+bcosA = √(a²+b²)[sinA*a/√(a²+b²)+cosA*b/√(a²+b²)]

= √(a²+b²)[sinA*cosB+cosA*sinB], cosB = a/√(a²+b²), sinB = b/√(a²+b²)

= √(a²+b²)sin(A+B)

疊合之範例：5sinA+3cosA = √(5²+3²)sinB = √34sinB

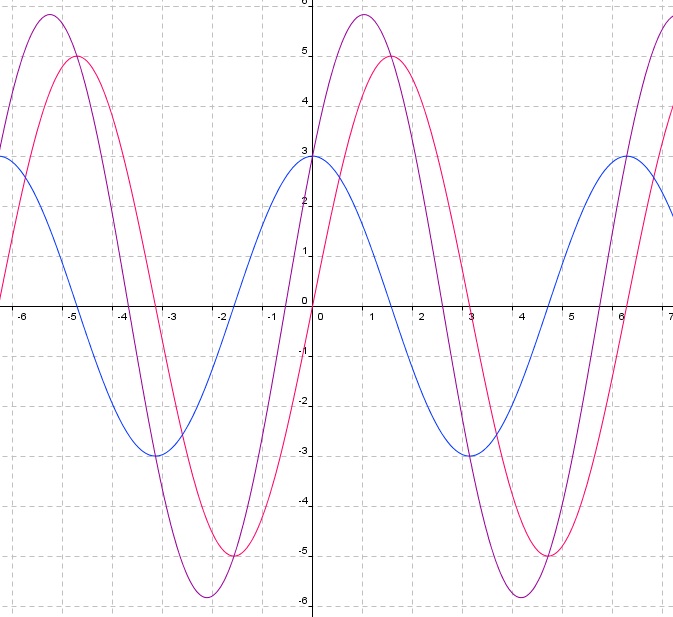
複數的極式

z = r(cosA+isinA) = re^iA, r≧0

隸美弗定理

zⁿ = (re^iA)ⁿ = rⁿe^inA = rⁿ(cosnA+isinnA), r≧0