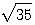=0，x2-3x-54=0，(1+
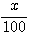)3=1.2分別是1次、2次、3次方程式。◎→多項方程式←◎
(1)由n次多項式到n次方程式
f(x)= anxn+an-1xn-1+…+a1x+a0 是n次多項式，方程式f(x)=0稱為n次(多項)方程式。
例如：3x-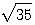=0，x2-3x-54=0，(1+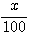)3=1.2分別是1次、2次、3次方程式。
(2)方程式的根：
一個數x0若滿足f(x0)=0，就稱x0為方程式f(x)=0的根或解。有時特別強調x0為複數、實數、有理數或整數，x0又稱為複數根、實根、有理根或整數根。
(3)實根的幾何解釋：
例如：(1)y=f(x)=x2-3x-4的圖形，如右圖所示：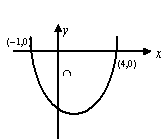 
圖形與x軸相交於兩點(-1,0)、(4,0)，其橫坐標-1與4就是x2-3x-4=0的實根。
(2)y=g(x)=x2+x+1的圖形，如右圖所示： 
圖形與x軸沒有交點，因為y=g(x)=(x+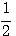
)2+
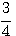，所以沒有任何實數x，使得g(x)=0，故g(x)=0沒有實根。方程式x2+x+1=0 的解x= 
。
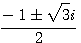一般而言，n次多項式y=f(x)的圖形是一條波浪形、平滑的連續曲線。若該曲線和x軸相交，那麼交點P(x0,f(x0))的橫坐標x0必滿足f(x0)=0，所以x0是方程式f(x)=0的一個實根，如果該曲線與x軸沒有交點，此時任何實數均不是方程式f(x)=0的根，因此方程式f(x)=0無實根。
實係數n次方程式f(x)=0的實根a Ûn次函數y=f(x)的圖形與x軸交於點(a,0)
例子：
x2-5x+6=0 x=2或3
x2+x+1=0
x=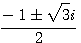
x3-x2+4x-4=0 (x-1)(x2+4)=0 Þx=1，2i,-2i
x4+5x2+4=0 (x2+1)(x2+4)=0 Þx=i ,-i,2i,-2i
(1)實係數n次方程式虛根成對：
定理一：若f(x)=anxn+an-1xn-1+…+a1x+a0為一實係數n次多項式，z為一個複數，則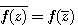
。
引理1：若z1,z2為二複數，則(a)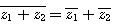
(b)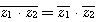 
。
引理2：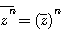
，其中n為正整數。
定理二：設f(x)=anxn+an-1xn-1+…+a1x+a0=0為一實係數n次方程式，若z為f(x)=0的一根，則共軛虛數 
亦為f(x)=0的一根。
[討論]：
(a)若f(x)=0為一個3次的實係數方程式，是否一定有實根呢？
(b)若f(x)=0為一個4次的實係數方程式，是否一定有實根呢？
一般的情形：
(a)若f(x)=0為一個奇數次的實係數方程式，一定有實根。
(b)若f(x)=0為一個偶數次的實係數方程式，一定有偶數個實根。(可能沒有實根)
(2)有理根成對：
先舉一個例子：
設f(x)=x4-6x3+7x2+6x-2
(a)驗證2+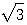
是有理係數f(x)=0的一個無理根。
(b)取g(x)=[x-(2+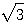
)][x-(2-
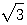)]=x2-4x+1，請問f(x)是否能被g(x)整除？
(c)請問2-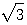
是否為f(x)=0的另一個無理根。
一般情形：
設f(x)為有理係數多項式，a,b為有理數，且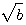
為無理數
若x=a+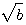
為f(x)=0之一根，則 x=a-
亦為其根。
(1)整係數的n次方程式找有理根：
(a)一次因式檢驗定理：
設f(x)=anxn+an-1xn-1+…+a1x+a0為一個整係數n次多項式，若整係數一次式ax-b是f(x)的因式，且a,b互質，則a|an且b|a0。
(b)有理根檢驗定理：
設f(x)=anxn+an-1xn-1+…+a1x+a0=0為一個整係數n次方程式，若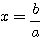
為f(x)=0之一有理根，a,b為整數且互質，則a|an且b|a0。
(2)無理根的問題：
利用整係數一次因式檢驗定理，可解決有理根的問題，但是就一般的方程式而言，要找出解，尤其是高次的方程式，通常不是一件容易的事情。
勘根定理：
設f(x)=0為實係數n次多項方程式，a,b是兩個實數，若f(a)×f(b)<0，則在a,b之間至少有一個f(x)=0的實根。
[定理的說明]：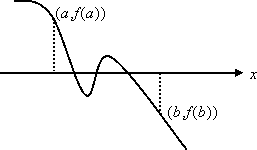
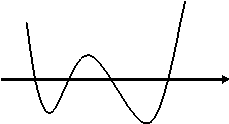
注意：
1. 從觀察圖形可知，當f(a)×f(b)<0時，則a,b之間的根必有奇數個根。
2. 從圖形的觀察，當f(a)×f(b)>0時，f(x)=0在a,b之間可能有根，也可能無根，但若有根一定是偶數個根。
[方程式的引入] [多項方程式解的性質] [解根的方法] [返回<多項式麻將至尊>]