◎→最高公因式與最低公倍式←◎

◎→最高公因式與最低公倍式←◎

[因式與倍式] [公因式與公倍式]

(1)定義：設f(x),g(x)為二多項式，若存在多項式h(x)使得f(x)=g(x)×h(x)，則稱f(x)為g(x)的因式或g(x)為f(x)的倍式。符號：f(x)|g(x)。

例如：因為x³-1=(x-1)(x²+x+1)，所以x-1與x²+x+1均為x³+1的因式，x³+1為x-1與x²+x+1的倍式。

例如：因為 = = ，所以x+1，x+2，，都是的因式。

注意：由上面兩個例子可知，若f(x)|g(x)，則c×f(x)|g(x)(c¹0)。因此就一般而言，只要求出整係數的因式或倍式即可。

(2)性質：若設d(x)|f(x)，d(x)|g(x)，則d(x)|m(x)×f(x)+n(x)×g(x)。

(1)公因式與公倍式：

1. 若多項式d(x)同時為多項式f(x),g(x)的因式，則稱d(x)為f(x),g(x)的公因式。

注意：d(x)=c (c¹0)為任何兩個多項式的公因式。

設d(x) 為f(x),g(x)的公因式，則k×d(x)(k¹0)亦為f(x),g(x)的公因式，因此我們通常只取一個代表就行了。

2. 如果多項式f(x),g(x)除了常數以外，沒有其它的公因式，就稱它們互質。

設f(x),g(x)都是非零多項式，如果m(x)同時是f(x),g(x)的倍式，那麼就稱m(x)為f(x),g(x)的公倍式。設m(x) 為f(x),g(x)的公倍式，則k×m(x)亦為f(x),g(x)的公倍式，因此我們通常只取一個代表就行了。

例如：設f(x)=4x²-1,g(x)=4x²+4x+1,h(x)=2x²-7x+3。求f(x),g(x)的公因式，g(x),h(x)的公因式。

因為f(x)=(2x+1)(2x-1)，g(x)=(2x+1)²，h(x)=(2x-1)(x-3)，所以2x+1,x+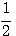，4x+2…等凡是k(2x+1)的形式都是f(x),g(x)的公因式。在g(x),h(x)中，除了常數外沒有其它的公因式，故g(x),h(x)互質。

(2)最高公因式、最低公倍式：

1. 設f(x),g(x)為兩多項式，如果d(x)是它們公因式中次數最高的，那麼稱d(x)為最高公因式(H.C.F)，符號：(f(x),g(x))=d(x)。

注意：

A. 當多項式f(x),g(x)互質時，符號：(f(x),g(x))=1。

B. 最高公因式與公因式一樣，並不是只有一個，不過任兩個最高公因式之間都只差一個常數因式，因此通常所謂兩個多項式的最高公因式，可取它們的任意一個最高公因式。

C. 設f(x),g(x)為兩多項式，如果m(x)是它們公倍式中次數最低的，那麼稱m(x)為最低公倍式(L.C.M)，符號：[f(x),g(x)]=m(x)

注意：最低公倍式也不是唯一的，不過它們之間也都只差一個常數因式。

(3)H.C.F與L.C.M的求法：

1. H.C.F的求法：

A. 因式分解法：

將各個多項式分別因式分解，再取其中公因式相乘，即可得到H.C.F。

例如：f(x)=(x²-x+3)(x+4)(x-5)(x+1)，g(x)=(x²-x+3)(2x-3)(x+6)(x-5)則f(x)與g(x)的最高公因式為(x²-x+3) (x-5)

B. 輾轉相除法：

設f(x)，g(x)為二多項式，且g(x)¹0，則由除法定理可知：恰有兩個多項式q(x),r(x)滿足f(x)=g(x)×q(x)+r(x)，其中r(x)=0或deg r(x)<deg g(x)。

原理：(f(x),g(x))=k×(g(x),r(x))。k¹0

C. 因式的性質：

若設d(x)|f(x)，d(x)|g(x)，則d(x)|m(x)×f(x)+n(x)×g(x)。

2. L.C.M的求法：

A. 因式分解法：

先將各多項式因式分解，再取出最低公倍式。

例如：f(x)=(x²-x+3)(x+4)(x-5)(x+1)，g(x)=(x²-x+3)(2x-3)(x+6)(x-5)則f(x)與g(x)的最低公因式為(x²-x+3) (x-5)×(x+4)(x+1)(2x+3)(x+6)

B. 輾轉相除法：

利用輾轉相除法，求出f(x)與g(x)的H.C.F 為d(x)，則f(x)與g(x)的L.C.M=。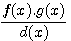

原理：f(x)×g(x)=k×(f(x),g(x))×[f(x),g(x)]