◎→多項式的四則運算←◎
(1)何謂多項式：
在代數中，我們通常會引進一些符號x,y,z等，用以表示一給定問題的未知數，有了這一些符號，可將問題中量與量之間的關係列成算式，而將給定的問題轉成方程式的問題，而在解方程式的過程中，跟數一樣，會牽涉到數與式之間的運算。將數及具有數的性質的符號x,y,z等，經過加、減、乘的運算所形成的式子，叫做多項式。多項式中，只含有一個符號x，叫做單元多項式，含有多於一個的符號，叫做多元多項式。
若an,an-1,…a1,a0均為實數，n為非負整數，形如anxn+an-1xn-1+…+a1x+a0 稱x的單元多項式，也可簡稱為x的多項式。
設f(x)= anxn+an-1xn-1+…+a1x+a0
(2)相關的名詞說明：設f(x)=anxn+an-1xn-1+…+a1x+a0為x的多項式
1.項：anxn,an-1xn-1，…,a1x,a0分別稱為此多項式的n次項,n-1次項,…一次項,常數項。
2.係數：an,an-1,…,a1,a0分別為此多項式的n次項,n-1次項,…一次項,常數項的係數。
3.領導係數：多項式中最高次項之係數(不為0)稱為此多項式之領導係數。
4.次數：當an¹0時，稱此多項式為n次多項式，記為：deg f(x)=n。
5.單項式：只有一項的多項式稱為單項式。
6.常數多項式：若一多項式僅含常數項a0，則稱此多項式為常數多項式。當a0¹0，又稱 為零次多項式。當a0=0，又稱為零多項式。
7.升羃與降羃式：若一多項式一變數x的次方由大而小排列者稱為降羃式，由小而大 排列者稱為升羃式。
(3) 由多項式的係數決定多項式全體所成的集合：
Z[x]表由整係數多項式全體所成的集合
Q[x]表由有理係數多項式全體所成的集合
R[x]表由實係數多項式全體所成的集合(主要討論實係數多項式)
C[x]表由複係數多項式全體所成的集合
(4)多項式的相等：
兩個多項式f(x)與g(x)為兩個非零多項式若f(x)與g(x)相等Û兩者的次數相同，對應項的係數也一樣。
(1)多項式的加減法：兩多項式相加減，則同次項的係數相加減。
例如：f(x)=6x4-7x3+2x+7，g(x)=-5x5+2x3-3x2+8x-9
f(x)+g(x)=
f(x)-g(x)=
deg (f(x)±g(x)) £ Max(deg f(x),deg g(x))或f(x)±g(x)=0
(2)多項式的乘法：利用乘法對加法的分配律，再合併同類項。
例如：f(x)=3x3-2x2+x-4，g(x)=4x2-6x+1
直式運算：f(x)×g(x)
橫式運算：f(x)×g(x)
deg (f(x)×g(x))=[deg f(x)]×+ [deg g(x)] (其中f(x)與g(x)均不為零多項式。)
(3)多項式的除法：
設f(x)，g(x)為二多項式且g(x)不是零多項式，則可找到二多項式q(x)及r(x)滿足f(x)=q(x)×g(x)+r(x)，其中r(x)=0或deg r(x)<deg g(x)。
此時稱f(x)為被除式，g(x)為除式，q(x)為商式，r(x)為餘式。
例如：設f(x)=2x3+5x2+x-2，g(x)=x2+2x-3
分離係數法：
(4)綜合除法：當除式g(x)=x-a時，我們介紹綜合除法去求商式、餘式。
設f(x)=2x4+x2-5x，g(x)=x-2，求f(x)除以g(x)的商式、餘式。
綜合除法的原理：
設f(x)=a3x3+a2x2+a1x+a0，g(x)=x-b，若存在商式q(x)=c2x2+c1x+c0，餘式r(x)=d。
由除法的定義：(a3x3+a2x2+a1x+a0)=( c2x2+c1x+c0)( x-b)+d
經比較係數可得：
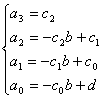
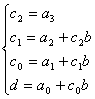
上面的關係可寫成以下的形式：
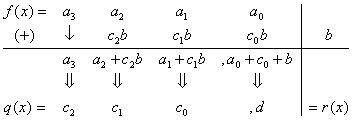
當f(x)除以g(x)=ax+b時，我們也可利用綜合除法求餘式r(x)、商式q(x)。
由除法的定義：f(x)=(ax+b)×q(x)+r(x)=(x+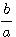
)×[aq(x)]+r(x)可先利用綜合除法求出f(x)除以(x+
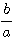)的商式q/(x)=aq(x)與餘式r(x)，而所要求的商式q(x)=
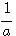q/(x)，餘式r(x)不變。
例如：f(x)=3x3+5x2-46x+42除以g(x)=3x-7
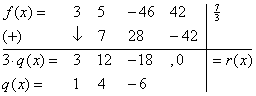
多項式的係數和：
f(x)= anxn+an-1xn-1+…+a1x+a0，則各項係數之和=f(1)，常數項=f(0)
奇次項係數之和=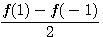 
，偶數項的係數之和=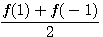 
f(i)之實部=a0-a2+a4-a6+…..，f(i)之虛部=a1-a3+a5-a7+….
[多項式的基本定義] [多項式的運算] [返回<多項式麻將至尊>]