運算思維：一張圖看懂機器翻譯（人工智慧）的原理

報載自107學年度起，教育部要將「程式設計」納入國中小的課程，從小培養學生的「運算思維」 （Computational Thinking）。

近幾年來，全球各國都在推動運算思維，以便讓現代國民可以融入未來更為普及的資訊社會， 甚至是人工智慧無所不在的社會。

運算思維的概念，網路上介紹很多，不再熬述。在此，根據個人的經驗， 提出幾個較為核心的能力與概念，包括：

1. 把待解任務定義清楚，變成可以計算（用電腦解決）的問題，此為 「問題定義」 （problem formulation ）的能力。這跟數學的訓練很相關。 從小我們在解數學的應用問題時，便是在將文字敘述的情境， 轉換成用數學的加減乘除等技術可以解決的問題。
2. 有了可計算的問題，再將該問題分解成較小而易解的小問題、小步驟， 亦即「問題分解」（decomposition）或是「各個擊破」（Divide and Conquer）的能力。
3. 充分利用電腦能夠高速計算（與儲存大量資料）的能力，來解決問題。 其中一種利用方法，概念上很簡單，可稱為「暴力法」（ brute force）或是「窮舉法」（enumeration），也就是讓電腦把各種可能性都考慮過，然後從中找出最佳的解法。學計算機工程的人要學演算法（Algorithm），以便讓計算速度變快。但一般人只要懂這個窮舉法，就可以用電腦解決很多問題。

用前一陣子下圍棋勝過職業棋手的AlphaGo為例，其在棋局的末段，只要用窮舉法讓電腦可在預定的時間內算完所有可能的對奕情況，人類就不可能贏，最多沒犯任何錯誤，跟電腦打成平手而已。更簡單的五子棋，也是從頭到尾用窮舉法即可，人類就不可能贏電腦。窮舉法讓電腦下起棋來，看起來就很有智慧的樣子。

好了，現在來看一個比較實際的例子：運用電腦來做自動翻譯。 如下圖所示：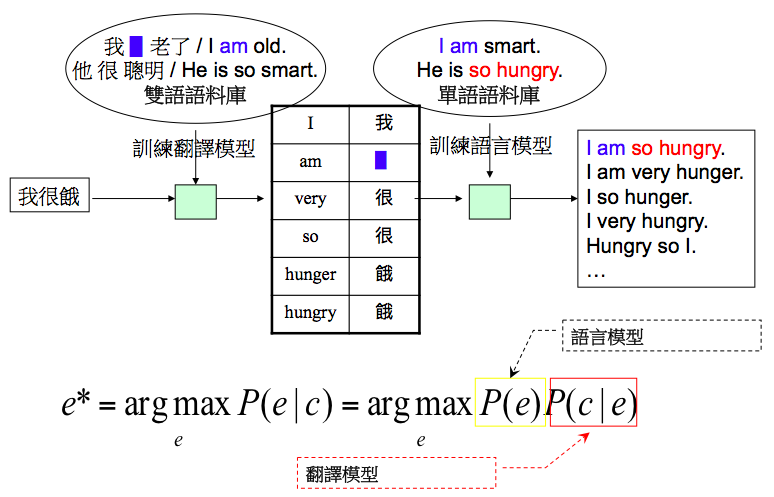

假設我們要將中文的「我很餓」翻譯成英文的「I am so hungry」，要怎麼做呢？ 首先，把這項任務變成可計算的問題，亦即表達成：

先不要被這個式子嚇到，它只是在說，當我們看到一句中文 c 的時候，可去找出很多對應的英文 e ，然後算出其條件機率，亦即 P(e|c)。之後，再從眾多的P(e|c)中，找出其中機率最高的那個 e* 即可。這個步驟對應到上述的第一點：「問題定義」（problem formulation）。

但是機率 P(e|c) 要怎麼算呢？根據貝氏定理（Bayes Theorem），我們可以把這個問題，分解成計算 P(c|e) 乘以 P(e)。這時，用到的不是簡單的加減乘除而已，還要知道貝氏定理，就如同在幾何學算土地的邊長時，有時需要知道畢氏定理一樣。

那P(c|e) 跟 P(e) 要怎麼計算呢？光看條件機率 P(c|e) 就知道我們好像碰到跟算P(e|c)的問題一樣，那不是在原地打轉嗎？

這時，我們再運用一次「分解」的概念，計算近似值即可。先看P(e)怎麼算（假設 e="I am so hungry"）：

亦即e這個句子的機率，是個別詞彙出現機率的乘積。這種近似方式，稱做「單字詞語言模型」（unigram language model）。它只要統計附件圖中的「單語語料庫」（English corpus）中，出現這些詞彙的機率，即可算出 e 這個句子的機率。（還有其他更準確的語言模型，如雙連詞語言模型可用，在此先略過不講）

同理，運用分解的概念，我們也可以計算條件機率 P(c|e) 的近似值：

P("很" | "so") 這類條件機率，稱為「翻譯模型」，這要蒐集「雙語語料庫」，然後列出中、英文詞彙對應表（如圖中的表），再統計對應詞彙的條件機率，就可算出 P("我很餓" | "I am so hungry") 的近似值。在此，若我們只有如圖中對應好的中英文句子，沒有對應好的中英詞彙，可用窮舉法把對應的句子中的詞彙，任意配對，只要雙語語料庫夠大，P("很" | "so") 的機率就會高過P("很" | "hungry") 的機率，然後我們就可知道要挑P("很" | "so")這個條件機率來用。

上述的「翻譯模型」，讓我們從一句中文，（窮舉）組合出很多句候選的英文字串。再透過「語言模型」，讓我們從眾多候選的英文字串中，找出最常出現、最合乎英文文法的句子，亦即其有最高的機率值。由翻譯模型組合出來的候選句子，如圖中的：「I am very hunger」、「I so hunger」的機率，在語言模型中，應該都不如「I am so hungry」高。據此，我們就可以自動將「我很餓」，找出（翻譯成）「I am so hungry」的對應句子了。