manifold（topological surface）

「流形」。伸縮自在的表面。

set peoperty
1. closed/closure: only 1 connect component (and contain limit point)
2. bounded/boundary: cannot reach infinite
3. compact: closed + bounded

orientation:
1. mobius band
2. klein bottle
https://en.wikipedia.org/wiki/File:Flatsurfaces.svg

genus:
1. shpere = 0
2. torus = 1

embedding:
drawing

gauss map / turning number / total curvature
法向量畫到圓上，看看繞幾圈
封閉曲線的繞行角度一定是2π的整數倍

gauss-bonnet theorem
1. closed curve   ∫Ω κ ds = 2π k
2. closed surface ∫ᴍ K dA = 2π χ(M)   where χ(M) = 2 - 2g
表面的高斯曲率總和

fundamental group

1. fundamental group: basis of all cycles through a point
2. homotopy group: fundamental group generalization
3. homology group: non-degenerated cycles under homotopy???
4. #(fundamental group) = 2g

tree-cotree decomposition [Eppstein 03]
spanning tree on planar graph / fundamental cycle basis
1. spanning tree T in primal graph
2. spanning cotree T* in dual graph (not cross edges of T)
3. for any edge not contained in T and not crossed by T*,
   follow both of its vertices to the root T, a fundaemental cycle.

Euler characteristic χ = V - E + F = 2 - 2g
spanning tree T:    V-1 edges
spanning cotree T*: F-1 edges
remaining edges: E - (V-1) - (F-1) = -(2 - 2g) + 2 = 2g

orbifold

orbifold / orientation
http://geometry.cs.cmu.edu/ddgshortcourse/AMSShortCourseDDG2018_DiscreteMappings.pdf

function

函數是「對應」與「變換」兩種概念的結合。

對應。mapping。

數量：one-to-one, many-to-one, one-to-many
　　　其中one-to-one又叫做injective
範圍：into, onto
　　　其中onto又叫做surjective
方向：invertible = one-to-one + onto
　　　其中invertible又叫做bijective = injective + surjective

變換。transformation。

鄰居：continuous
柔順：differentiable
量級：analytic

輸入輸出。

相同相異：self-mapping, non-self-mapping
　　　　　其中self-mapping又叫做autojective
宏觀微觀：global, local
　　　　　其中global經常省略不寫

function of manifold

可以想成是引入了子空間。函數的輸出輸入是子空間。

流形的函數。由於流形本身是函數，所以這其實是泛函數。

對應。mapping。

態射morphism = continuous
同胚homeomophism = bijective and continuous = bicontinuous
微分同胚diffeomorphism = bijective and differentiable and continuous
https://math.stackexchange.com/questions/1672786/

變換。transformation。

同倫homotopy = continuous
同痕isotopy = bijective and continuous (volumn preserving)
可微同痕differentiable isotopy = bijective and differentiable and continuous
https://math.stackexchange.com/questions/296170/

local

locally continuous injective is locally continuous bijective?
locally homeomoprhism is locally continuous and locally bijective.
locally bijective homeomorphism is globally bijective homeomorphism.

differentiable manifold

流形本身是函數，可以微分得到切面。

derivative = Jacobian
immersion  = 輸出入先做derivative, the new mapping everywhere is injective
submersion = 輸出入先做derivative, the new mapping everywhere is surjective

harmonic manifold

local bijection  iff  det(jacobian) > 0  everywhere
global bijection & convex  iff  coordinate is non-negative  everywhere
(diffeomorphism: X->Y is harmonic and Y is convex)

deformation（topology-preserving transformation）

改變物體形狀，符合真實情況。

目前沒有定論！大致能想到的有：

不斷裂：continuous        可逆不斷裂：bicontinuous
不重疊：injective         可逆不重疊：可逆不斷裂即滿足可逆不重疊
不打結：regular homotopy  可逆不打結：regular isotopy
不鏡射：right-handed?     可逆不鏡射：可逆不打結即滿足可逆不鏡射？

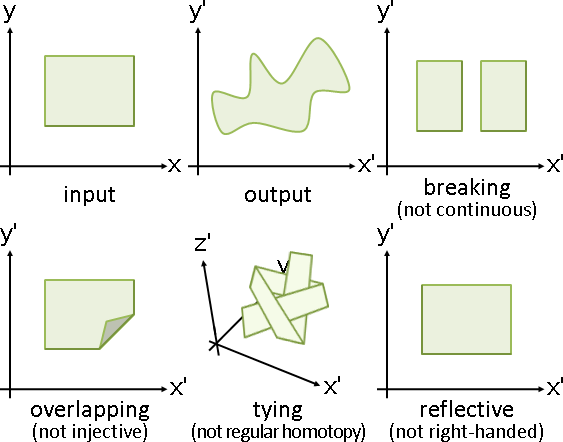
這些主題，目前依然存在許多謎題。靠你了。

不斷裂不重疊（continuous injective）

一維：嚴格單調。高維：性質尚待解明。

一、連續函數的情況下：
　　一維：單射＝嚴格單調
　　高維：單射＝高維嚴格單調＝任意截面都是嚴格單調？
二、連續自射函數的情況下：
　　一維：單射＝雙射＝嚴格單調
　　高維：單射＝雙射＝高維嚴格單調＝任意截面都是嚴格單調？

continuous injective = continuous strictly monotone
https://math.stackexchange.com/questions/279672/
https://math.stackexchange.com/questions/170147/

continuous injective self-mapping = continuous bijective
https://mathoverflow.net/questions/273632/
https://math.stackexchange.com/questions/541082/

可微的情況下，可以引入斜率、梯度。

三、連續可微函數的情況下：
　一維：單射＝嚴格單調＝處處斜率為正數、或者處處斜率為負數
　高維：單射＝高維嚴格單調＝無奇點的和諧函數？
四、連續可微自射函數的情況下：
　一維：單射＝雙射＝嚴格單調＝斜率處處正數或者處處負數
　高維：單射＝雙射＝高維嚴格單調＝無奇點的和諧函數？

continuous differentiable bijective = harmonic without singular point (?)
https://math.stackexchange.com/questions/61099/

不斷裂不重疊不鏡射（continuous injective nonreflective）

一維：嚴格遞增。高維：不知為何？

必須定義方位，才能定義鏡射。要求不斷裂不重疊，就能定義方位，就能定義鏡射？

局部不斷裂（locally continuous）

只看局部，又是另一套數學系統。

locally continuous：拓樸
locally differentiable：反函數定理

局部不斷裂，有可能局部重疊，例如扭捏重疊。

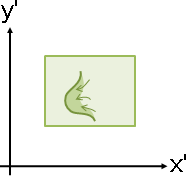
局部不斷裂不重疊（locally continuous injective）

局部不斷裂不重疊，但是全域可能重疊，例如螺旋重疊。

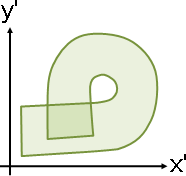
延伸閱讀：local everywhere vs. global

「局部處處」與「全域」之間，已經發現許多關聯，也依然存在許多謎題。數學家目前只知道單向結論：

四、連續可微自射函數的情況下：
　高維：處處梯度可逆、且函數邊界數值趨近無限，導致全域雙射。
　高維：處處梯度正定∇F≻0，導致全域單射。
　高維：處處梯度對稱正定∇F=∇Fᵀ≻0，導致全域雙射。
　高維：處處梯度行列式恆正det(∇F)>0，導致全域雙射？

∇F is locally bijective everywhere and boundary(F) approaches ±∞ ⇒ globally bijective
https://math.stackexchange.com/questions/41551/

∇F is locally positive-definite everywhere ⇒ globally injective
https://math.stackexchange.com/questions/1820156/
https://math.stackexchange.com/questions/1372692/

∇F is locally symmetric positive-definite everywhere ⇒ globally bijective
https://math.stackexchange.com/questions/2874445/

knot

repulsive curves
https://www.cs.cmu.edu/~kmcrane/

UVa 1624