substring - 演算法筆記

string searching

運用移位來處理字串搜尋問題

string searching（string matching）

「字串搜尋」、「字串匹配」。長字串T、短字串P，從T當中找到P的位置。

字串搜尋當中，我們習慣將兩字串的象徵符號取做T和P。T代表text，P代表pattern。

T: ababcabc
P: abc

ababcabc    ababcabc
  |||            |||
  abc            abc

T中有兩個地方出現P。

最直覺的演算法就是窮舉法：挪動P，對準T的各個位置；逐一比對字元、判斷是否相等。時間複雜度O(TP)。

T: ababcabc
P: abc

0.         1.         2.         3.         4.         5.
ababcabc   ababcabc   ababcabc   ababcabc   ababcabc   ababcabc
|||         |||         |||         |||         |||         |||
abc         abc         abc         abc         abc         abc
(X)         (X)         (O)         (X)         (X)         (O)

string searching: Morris–Pratt algorithm

想法

1.
T: aabzabzabcz
P: abzabc

2.
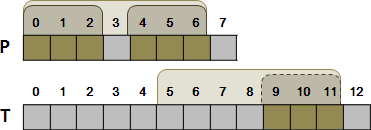
窮舉法，從左往右逐步挪動P。

  aabzabzabcz   aabzabzabcz   aabzabzabcz
  ||||||         ||||||         ||||||      ......
  abzabc         abzabc         abzabc
      (X)           (X)           (X)

2.
仔細看窮舉法，是從左往右一一比對字元，一旦發現字元不同，就馬上往右挪動P。

  V              V            V              V        
  aabzabzabcz   aabzabzabcz  aabzabzabcz   aabzabzabcz
  |             |X            |             ||        
  abzabc        abzabc        abzabc        abzabc    

     V             V               V             V    
  aabzabzabcz  aabzabzabcz   aabzabzabcz   aabzabzabcz
   |||          ||||          |||||         |||||X    
   abzabc       abzabc        abzabc        abzabc    

    V             V              V              V     
  aabzabzabcz  aabzabzabcz   aabzabzabcz   aabzabzabcz
    X             X              |             ||       ......
    abzabc        abzabc         abzabc        abzabc 

3.
往右挪動P之前，當下比對成功的字串片段，abzab，其實可以好好利用！

         V
   aabzabzabcz    -abzab-----
    |||||X         |||||
    abzabc         abzab-

4.
觀察窮舉法的步驟順序，繼續往右挪動P，挪動一個位置、挪動兩個位置、……。

  -abzab-----   -abzab-----   -abzab-----
    ||||           |||            ||     
    abzab-         abzab-         abzab- 

   -abzab-----   -abzab-----
        |                   
        abzab-         abzab-

5.
換個觀點觀察上述行為。
挪動一個位置：看看abzab的後四個字元，是不是前四個字元。
挪動兩個位置：看看abzab的後三個字元，是不是前三個字元。
　　　⋮　　　　　　　　　⋮　　　　　　　　　　⋮

6.
如果我們預先知道abzab的「次長的相同前綴後綴」是ab，
就可以一口氣大幅挪動P，略過許多步驟：

        V                 V
  aabzabzabcz        aabzabzabcz
   |||||X      --->      ||
   abzabc                abzabc

7.
從「V」處繼續向右一一比對字元。
每當比對失敗、遇到相異字元，
就故技重施，從當前比對成功的字串片段，取其「次長的相同前綴後綴」，大幅挪動P。

prefix-suffix【尚無正式名稱】

前綴等於後綴，稱作「相同前綴後綴」。一個字串通常有許多個「相同前綴後綴」。

         prefix-suffix
abc     --------------> {Ø, abc}
abcaa   --------------> {Ø, a, abcaa}
abcabc  --------------> {Ø, abc, abcabc}
ababa   --------------> {Ø, a, aba, ababa}
aaaaa   --------------> {Ø, a, aa, aaa, aaaa, aaaaa}
abaabaa --------------> {Ø, a, abaa, abaabaa}
abzab   --------------> {Ø, ab, abzab}

border（longest proper prefix-suffix）

一個字串的「最長的相同前綴後綴」就是原字串，「最短的相同前綴後綴」就是空字串，「次長的相同前綴後綴」就是第二長的相同前綴後綴。「次長的相同前綴後綴」簡稱「邊框」。

         border
abc     -------> Ø
abcaa   -------> a
abcabc  -------> abc
ababa   -------> aba
aaaaa   -------> aaaa
abaabaa -------> abaa
abzab   -------> ab

border table（prefix function）（failure function）

窮舉法的過程當中，當前比對成功的字串片段，是P的前綴。

因為我們無法預測是P的哪幾個前綴，所以我們可以預先計算P的每個前綴的邊框，預先建立「邊框表格」，以備不時之需！

   012345
P: abzabc

prefix | border | border table   | implementation
-------|--------|----------------|----------------
Ø      | Ø      | f(Ø)      = Ø  | 
a      | Ø      | f(a)      = Ø  | border[0] = -1
ab     | Ø      | f(ab)     = Ø  | border[1] = -1
abz    | Ø      | f(abz)    = Ø  | border[2] = -1
abza   | a      | f(abza)   = a  | border[3] =  0
abzab  | ab     | f(abzab)  = ab | border[4] =  1
abzabc | Ø      | f(abzabc) = Ø  | border[5] = -1

border table的演算法是dynamic programming。利用已知邊框，求得當前邊框。分割問題的方式是p[0...i]拿掉尾端字元p[i]。

【註：取名border table，由於函數輸出是border。取名prefix function，由於函數輸入是prefix。取名failure function，由於比對失敗就會使用它。】

演算法

一、預先計算P的每種前綴的「次長的相同前綴後綴」。
二、從左往右，依序比對字元。
　回、當比對成功、遇到相同字元：
　　　繼續比對下個字元。
　回、當比對失敗、遇到相異字元：
　　　從比對成功的字串片段，取其「次長的相同前綴後綴」，大幅挪動P。
　回、當全部比對成功、搜尋到P：
　　　就從比對成功的P，取其「次長的相同前綴後綴」，大幅挪動P。

時間複雜度

一、border table：字元兩兩比對次數最多2P次。

當比對成功，邊框長度增長；當比對失敗，邊框長度減短。總共增長P次、最多減短P次。邊框長度最多變動2P次。邊框長度變動次數即是字元兩兩比對次數。

二、字串搜尋：字元兩兩比對次數最多2T次。

原理同上。「邊框長度」改成「比對成功的字串片段長度」。

總時間複雜度O(T+P)。

UVa 455 10298 11475

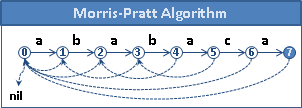
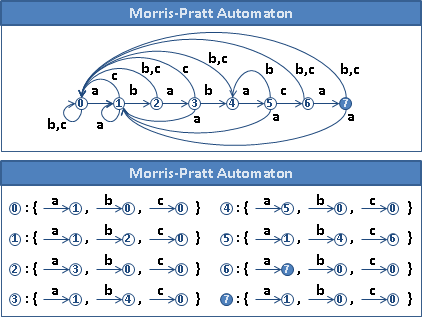
Morris–Pratt automaton

此演算法可以化作自動機，轉化的時間複雜度是O(PA)，A為字元種類數目。

針對每個狀態，找出經由border table能到達的狀態們；建立轉移邊，連到那些狀態們的下一個狀態。

化作自動機之後，字串搜尋變得非常簡單，容易製作成電路。

ICPC 4842

multiple string searching: Aho–Corasick algorithm

multiple string searching（multi-pattern string matching）

「多重字串搜尋」。一口氣搜尋P₁ ... Pₙ。

最直覺的演算法就是n次Morris–Pratt algorithm，時間複雜度O((T+P₁) + ... + (T+Pₙ)) = O(Tn+P)。

以下介紹更快的演算法，時間複雜度O(T+P+K)。

prefix tree與suffix link

Morris–Pratt algorithm的進化版本。

所有P併成一棵trie。在所有P之中尋找「次長的相同前綴後綴」。「預先計算每個前綴的border」變成了「預先計算每個節點的suffix link」。

dictionary suffix link

【註：原始論文無此概念。】

字串搜尋，當搜尋到某個P，必須檢查其餘P是否也相符。

一、若P不含父子字串：不需要檢查。

二、若P包含父子字串（一個字串是另一個字串的子字串）：每個節點必須額外行走suffix link，以找到所有相符的P。

額外添上dictionary suffix link，以迅速找到所有相符的P。

           suffix link：相同前綴後綴、不含自身、盡可能長。
dictionary suffix link：相同前綴後綴、不含自身、盡可能長、必須是某個P。

演算法

一、所有P建立一棵trie。
二、添上suffix link、dictionary suffix link。
三、拿T做字串搜尋：
　回、比對成功、遇到相同字元：走trie edge。
　回、比對失敗、遇到相異字元：走suffix link。
　回、找到所有相符的P：走dictionary suffix link。
　　（若P不含父子字串，則不需走。）
　　（只想找到任意一個相符的P，則不需走。）

時間複雜度

一、建立trie：O(P₁ + ... + Pₙ) = O(P)。

二、字串搜尋：O(T+K)。K是出現次數，最小是0，最大是O(Tn)。

總時間複雜度O(T+P+K)。

int N = 1000;	// P的個數
char T[100+1];
char P[1000][100+1];

bool occur[1000];	// 記錄各個P有沒有出現在T當中
int equiv[1000];	// 記錄各個P有沒有重複出現

struct TrieNode
{
	TrieNode* l[26], *suffix, *dictsuffix;
	int index;	// P的編號

TrieNode()
	{
		memset(l, 0, sizeof(l));
		suffix = dictsuffix = 0;
		index = -1;
	}
} *root;

// 初始化
void init()
{
	memset(occur, false, sizeof(occur));
	memset(equiv, -1, sizeof(equiv));
	root = new TrieNode();
}

// 砍掉整棵trie
void free(TrieNode* p = root)
{
	for (int i=0; i<26; ++i)
		if (p->l[i])
			free(p->l[i]);
	delete p;
}

// 把一個字串加入trie
void add(char* s, int index)
{
	TrieNode* p = root;
	for (; *s; ++s)
	{
		if (!p->l[*s - 'A'])
			p->l[*s - 'A'] = new TrieNode();
		p = p->l[*s - 'A'];
	}

// 如果此字串之前有出現，就特別記錄起來。
	if (p->index == -1)
		p->index = index;
	else
		equiv[index] = p->index;
}

// 添上suffix link和dictionary suffix link
// 以BFS順序進行
// 時間複雜度O(P)
void build()
{
	TrieNode* q[100000], **qf, **qb;
	qf = qb = q;
	*qb++ = root;

while (qf < qb)
	{
		TrieNode* p = *qf++;
		for (int i=0; i<26; ++i)
			if (p->l[i])
			{
				// 添上suffix link
				TrieNode* q = p->suffix;
				while (q && !q->l[i]) q = q->suffix;
				if (q) p->l[i]->suffix = q->l[i];
				else   p->l[i]->suffix = root;

// 添上dictionary suffix link
				TrieNode* r = p->l[i]->suffix;
				if (r->index != -1) p->l[i]->dictsuffix = r;
				else p->l[i]->dictsuffix = r->dictsuffix;

*qb++ = p->l[i];
			}
	}
}

// 拿trie與T進行字串搜尋
// 時間複雜度O(T+K)
void search(char* s)
{
	TrieNode* p = root;
	for (; *s; ++s)
	{
		// 不斷比對字元，直到比對成功。
		// 時間複雜度O(T)。
		while (p && !p->l[*s - 'A']) p = p->suffix;
		if (p) p = p->l[*s - 'A'];
		else p = root;

// 走dictionary suffix link找到所有相符的P。
		// 時間複雜度O(K)。
		for (TrieNode* q = p; q; q = q->dictsuffix)
			if (q->index != -1)
				occur[q->index] = true;
	}
}

void aho_corasick()
{
	init();		// 初始化
	for (int i=0; i<N; ++i)	// 所有P建立trie
		add(P[i], i);
	build();	// suffix link、dictionary suffix link
	search(T);	// 拿trie與T進行字串搜尋
	free();		// 釋放記憶體空間

for (int i=0; i<N; ++i)
		// 搜尋到P，或者之前出現過P。
		if (occur[i] ||
			equiv[i] != -1 && occur[equiv[i]])
			cout << "第" << i << "個字串有出現";
		else
			cout << "第" << i << "個字串沒出現";
}

UVa 10679 ICPC 4670

Aho–Corasick automaton

此演算法可以化作自動機，轉化的時間複雜度是O(NA)，N為trie的節點數目，A為字元總類數目。轉化原理如同Morris–Pratt automaton。

dictionary suffix link無法融入到自動機裡面，必須額外記錄。

UVa 11468 ICPC 3124 5103

wildcard searching: Pinter's algorithm

wildcard searching（wildcard pattern matching）

「萬用字元搜尋」。P含有萬用字元。

演算法

將P拆成一段一段不含萬用字元的字串，然後使用multiple string searching求出各小段在T中的出現位置，看看P的所有小段是否同時出現、是否位置不重疊。時間複雜度O(T+P+K)。

UVa 475 12785

2D string searching: Baker–Bird algorithm

2D string searching（2D pattern matching）

「二維字串搜尋」。T與P是二維長方形。

演算法

時間複雜度O(T+P)。

1.
把T橫切成一條一條，
把P橫切成一條一條，
然後每一條T都執行multiple string searching，例如Aho–Corasick algorithm。
如果第a條P，從T[i][j]開始出現，那麼就進行記錄：M[i][j] = a。
M是一個跟T一樣大的陣列。

2.
把M直切成一條一條，
每一條M都執行string searching，例如Morris–Pratt algorithm。
看看是否出現1234567...n這個字串（P總共n條）。

X.
當P有某兩條相同時，則要小心處理，把這兩條的編號設為相同。

附帶一提，如果使用Aho–Corasick algorithm，因為P不含父子字串，所以不必建dictionary suffix link，省下很多功夫。

UVa 11019

string searching: Knuth–Morris–Pratt algorithm

演算法

          v
T: aaaabcacab
P:    abcabcacab
          ^

Morris–Pratt algorithm當中，當比對到上圖之處，c != b，所以需要向右挪動P。找到abca的「次長的相同前綴後綴」，也就是a。然後向右挪動P，最後左端凸出一段a，如下圖所示。

          v
T: aaaabcacab
P:       abcabcacab
          ^

接下來就繼續比對字元。在這裡c != b，所以又要挪動P了。

Knuth則是多想了一步：連續挪動P，能不能預先偵測呢？Knuth發現，找到abca的「次長的相同前綴後綴」a之後，看看a的下一個字元（是b），是否仍是abca的下一個字元（也是b）。如果兩個字元一樣，那就表示P鐵定會連續挪動兩次，兩次比較都是c != b。

既然鐵定會挪動兩次，那乾脆直接移到定位不就好了？於是Knuth在計算border table的時候，就額外加了一個判斷：找到abca的相同前綴後綴f(abca) = a之後，如果f(abca)的下一個字元恰巧仍是abca的下一個字元，那麼就令f(abca) = f(a)，也就是再多找一次a的相同前綴後綴。如此一來，P只要移一次就行了。

由於f()是遞迴定義，所以連續挪動三次、四次、五次的情況，經過遞迴計算，最後都會變成一次移到定位。

border table變慢、字串搜尋變快。時間複雜度仍是O(T+P)。

string searching: Boyer–Moore algorithm

演算法

每次向右挪動P，有著good-suffix shift與bad-character shift兩種挪動選項，選擇向右挪動較多者。

每次挪動P之後，從P的右端、往P的左端比對字元。

good-suffix shift

P的每個後綴，找到本身以外，最後出現的地方。

若沒重複出現，則找到「次長的相同前綴後綴」。即是border table，函數輸入變成後綴罷了。

計算good-suffix shift表格的時間複雜度是O(P)。

bad-character shift

P的每個字元，找到最後出現的地方。

注意到bad-character shift可能向左挪動。

計算bad-character shift表格的時間複雜度是O(P+A)。A為字元種類數目。

時間複雜度

字串搜尋，最差時間複雜度O(TP)，此時T與P的全部字元皆相同；最佳時間複雜度O(T/P)，此時T與P沒有共同的字元。

當T與P並非週期性字串，字元兩兩比對次數最多3T次。

號稱實務上最快的演算法。

可以直接使用C++標準函式庫的boyer_moore_searcher()。

string searching: Horspool's algorithm

演算法

只使用bad-character shift。容易實作。

可以直接使用C++標準函式庫的boyer_moore_horspool_searcher()。

multiple string searching: Wu–Manber algorithm

想法

硬是拿Horspool's algorithm來做多重字串搜尋。

比對單位改為B個字元，用hash function併為一數。

演算法

一、只看每個P的左端m個字元，暫時忽略右端其餘字元。
　　P長度最短者，取作m。
二、預先建立SHIFT table、HASH table、PREFIX table。
三、實施Horspool algorithm，
　　比對單位改為B個字元，挪動單位仍是一個字元。
　　直接從SHIFT table取值，判斷比對成功、比對失敗。
　回、B個字元比對失敗：
　　甲、SHIFT table，根據其值，向右挪動P。
　回、B個字元比對成功：
　　甲、P的後綴在T中：
　　　　HASH table，得到後綴是這B個字元的所有P。
　　乙、P的前綴在T中：
　　　　PREFIX table，得到這些P的前綴、B個字元，判斷是否也在T出現。
　　　　T的當前比對位置往左數m個字元，就能進行判斷了。
　　丙、P的其餘片段在T中（只有這裡是看P的全部字元）：
　　　　逐個字元比對，方向隨便。若找到整個P，就輸出。
　　丁、向右挪動P、一個字元。

SHIFT table

輸入B個字元，找到整個P之中最後出現的地方。

時間複雜度O(PB)，空間複雜度O(Aᴮ)，A是字元種類數目。

HASH table

輸入後綴、B個字元，得到符合條件的所有P。

時間複雜度、空間複雜度同SHIFT table。

PREFIX table

輸入其中一個P，得到前綴、B個字元。

時間複雜度O(nB)，空間複雜度O(n)，n是P的個數。

時間複雜度

字串搜尋，最差時間複雜度O(BTP)，此時T與P的全部字元皆相同。最佳時間複雜度O(BT/m)，此時T與P沒有共同的連續B個字元。

string searching: Gusfield's algorithm

common prefix

多個字串的相同前綴，稱作「共同前綴」。通常有許多個。

               common prefix
{abc, abcde}  --------------> {Ø, a, ab, abc}
{abc, ab, a}  --------------> {Ø, a}
{abc, bc, de} --------------> {Ø}

longest common prefix

多個字串的「最長共同前綴」。

                    lcp
{abc, abcde}  --------------> abc
{abc, ab, a}  --------------> a
{abc, bc, de} --------------> Ø

prefix table（z function）

s[0]開始的字串、s[i]開始的字串，兩者的最長共同前綴，儲存至「前綴表格」的z(i)。s[0 ... z(i)-1] = s[i ... i+z(i)-1]。

  | 0 1 2 3 4 5 6 7
--+-----------------
s | a b a a b a a b
z | 8 0 1 5 0 1 2 0

z(0)：abaabaab，長度8。
z(1)：Ø，長度0。
z(2)：a，長度1。
z(3)：abaab，長度5。

z(0)是整個字串的長度。由z(1)開始算。

計算z(i)，是運用已經算好的z(j)，j < i。也就是指已經算好的某一段s[0 ... z(j)-1] = s[j ... j+z(j)-1]。首先找出哪一段s[j ... j+z(j)-1]覆蓋了s[i]，而且j+z(j)-1越右邊越好。

一、如果沒有任何一段s[j ... j+z(j)-1]覆蓋了s[i]，表示已經算好的部份都派不上用場。從s[i]與s[0]開始比對，逐字比下去。

二、如果有一段s[j ... j+z(j)-1]覆蓋了s[i]，表示s[i]也會出現在s[0 ... z(j)-1]之中，把i映射到對應的位置i'。緊接著再來一次，運用z(i')，也就是指s[0 ... z(i')-1] = s[i' ... i'+z(i')-1]，如此又把i'映射到字串開頭了。

二之一、如果s[i ... i+z(i')-1]短少於s[j ... j+z(j)-1]的右端，那就可以直接算出z(i)的答案，就是z(i')。

二之二、如果s[i ... i+z(i')-1]剛好貼齊s[j ... j+z(j)-1]的右端，那就必須檢查不確定的部分，直接從s[j+z(j)]與s[j+z(j)-i]繼續比對，逐字比下去。

二之三、如果s[i ... i+z(i')-1]凸出了s[j ... j+z(j)-1]的右端，則與上一種情形相同。

j便是原著中的L，j+z(j)-1便是原著中的R。

演算法

製做P + $ + T，也就是說，P接到T開頭，中間用一個從未出現的字元隔開。然後算z()，看看哪些z(i)剛好是P的長度。

實作時，不必真的銜接T與P。先計算P的z()，再以此計算P + $ + T的z()。

時間複雜度

字元兩兩比對次數最多2(P+1+T)次。時間複雜度O(T+P)。

當比對成功，共同前綴長度增長；當比對失敗，長度減短。總共增長(P+1+T)次、最多減短(P+1+T)次。長度最多變動2(P+1+T)次。共同前綴長度變動次數即是字元兩兩比對次數。

Gusfield's algorithm vs. Morris–Pratt algorithm

Gusfield's algorithm：
最長共同前綴（longest common prefix）的表格（prefix table）
演算法是兩個步驟prefix(P,P)和prefix(T,P)

Morris–Pratt algorithm：
次長相同前綴後綴（longest proper prefix-suffix）的表格（border table）
演算法是兩個步驟border(P,P)和border(T,P)

UVa 11022 ICPC 4759

string searching: two way algorithm

演算法

cache-efficient algorithm。存取記憶體相當花費時間，節省記憶體以節省時間。不建立表格，額外記憶體空間是O(1)。

當表格沒有優勢，也就是說，當T與P不會重複出現子字串，那麼此演算法是實務上最快的演算法。

可以直接使用glibc的strstr()。水很深，此處不展開。