spiral

「螺線」。繞圈的曲線。

radial function
X and F(X) ⇨ angle and radius

繪製函數圖形，除了水平延展，還可以迴旋延展。

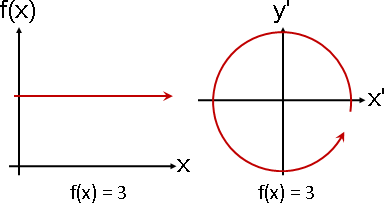
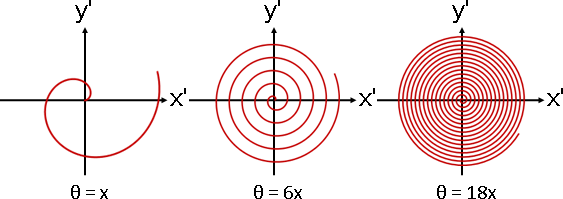
「徑向函數」。函數輸入視作從X軸出發的角度，函數輸出視作從原點出發的長度。

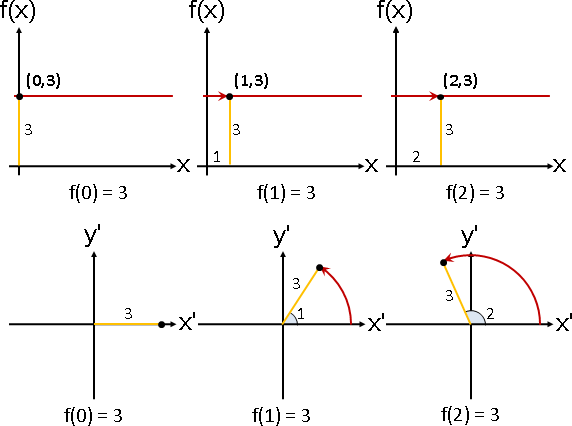
利用三角函數sin()和cos()找到繪製地點。

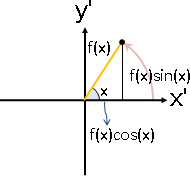
當函數輸出是負值，則無法畫出函數圖形。三種解法：一、乾脆不畫。二、負值變正值、換顏色。三、穿越原點，跑到對面，角度相差180度。

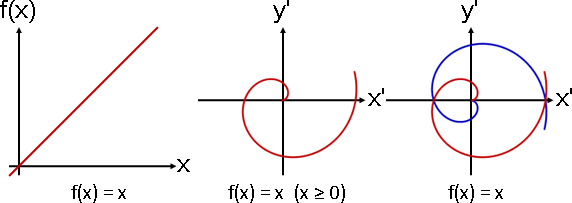
角度可以改成x的倍率，修改轉速。

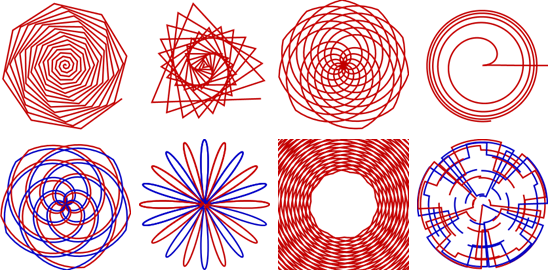
運用迴旋，得以製作許多特殊圖形。

periodicity ⇨ closed

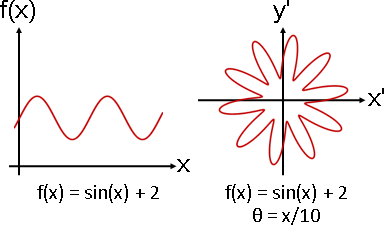
有個值得一提的案例是週期函數：固定間距、不斷重複的函數。

角度改成x的適當倍率，使得一個間距（或者其倍數）剛好轉一圈，函數圖形頭尾銜接，得到封閉曲線。

angle and radius ⇨ X and F(X)【查無專有名詞】

任意的封閉曲線，想要從迴旋延展變成水平延展，就必須滿足函數的規定：找到內部一點作為原點，任意放射線與曲線的交點只有一點。之後即可視作一般函數進行處理。

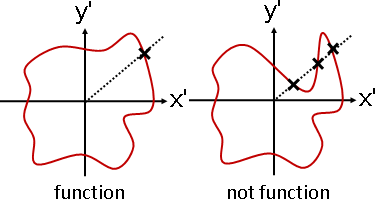
不是函數的封閉曲線，想要滿足函數的規定，我只知道一種解法是平滑化：每一個點，取其鄰點，求平均數。實施足夠次數，似乎就會變成函數。實施無限次，最後就會變成圓形，其概念類似於流形與圓的映射。我不清楚這部分是否有人研究。

sphere coordinates、函數輸入是兩個變數

函數輸入是兩個變數（或者一個複數），視作旋轉角度和俯仰角度，得到三維空間的表面。

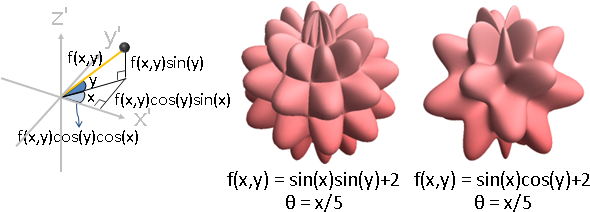
f[u_,v_] := Sin[u]Sin[v]+2; ParametricPlot3D[{f[u,v]Cos[v/5]Cos[u/5], f[u,v]Cos[v/5]Sin[u/5], f[u,v]Sin[v/5]}, {u, 0, 40}, {v, 0, 40}, Boxed -> False, Axes -> False, Mesh -> None, PlotPoints -> 70, ColorFunction -> (ColorData["CherryTones"][Rescale[#3, {-2, 2}]] &) ]

cylinder coordinates、函數輸出是兩個變數

函數輸出是兩個變數（或者一個複數），視作水平距離和垂直距離，得到三維空間的線。

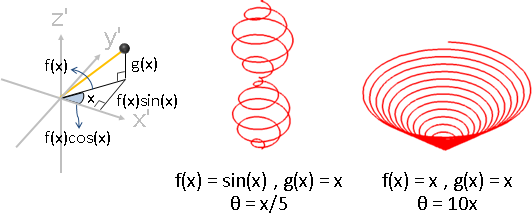
ParametricPlot3D[{Sin[x] Cos[x*10], Sin[x] Sin[x*10], x}, {x, 0, 9}, Boxed -> False, Axes -> False, PlotStyle -> {RGBColor[192,0,0], Thick}]

roulette

「旋輪線」。滾圈的曲線。

繪製旋輪線，除了水平延展，還可以迴旋延展。

https://www.zhihu.com/question/413178224/answer/1402560436

http://mathworld.wolfram.com/Roulette.html
https://en.wikipedia.org/wiki/Roulette_(curve)
https://en.wikipedia.org/wiki/Hypotrochoid
https://en.wikipedia.org/wiki/Brachistochrone_curve
https://en.wikipedia.org/wiki/Tautochrone_curve
https://en.wikipedia.org/wiki/Cycloid
https://en.wikipedia.org/wiki/Whewell_equation
https://en.wikipedia.org/wiki/Cesàro_equation
https://en.wikipedia.org/wiki/Catenary
https://en.wikipedia.org/wiki/Tractrix
https://en.wikipedia.org/wiki/Evolute

brachistochrone curve

「最速降線」。力與軌跡。

curvature = laplacian = stress

Bernstein polynomial

https://en.wikipedia.org/wiki/Hermite_polynomials

Chebyshev polynomial

Chebyshev polynomial: sine wave wrapped around a cylinder

Zernike polynomial

Taylor series

Δxⁿ projects onto basis, which is function gradient.

            f(x) (Δx)⁰   f′(x) (Δx)¹  f″(x) (Δx)²
f(x + Δx) = —————————— + —————————— + ——————————— + ...
                0!            1!           2!

Fourier series

「球諧函數」：傅立葉轉換的基底（各種頻率的複弦波），放到球座標系統進行迴旋，得到球諧函數。

「柱諧函數」。

Laplace equation

Legendre polynomial: Laplace's equation solution of sphere coordinate
Bessel Functions: Laplace's equation solution of cylinder coordinate
http://mathworld.wolfram.com/LaplacesEquationSphericalCoordinates.html
http://www.cs.jhu.edu/~misha/Spring19/

Hankel transform of Zernike polynomials are essentially Bessel functions

Poisson equation

[surface]
https://plot.ly/javascript/3d-surface-plots/
http://bl.ocks.org/supereggbert/aff58196188816576af0

Green's function
https://www.wolframalpha.com/input/?i=e%5E(i%7Cx-y%7C)+%2F+%7Cx-y%7C

e^(iκ|x-y|) / |x-y|

ΔG(x, y) + κ^2 G(x, y) = 0

Fourier curve

http://fourierart.com/
http://mathworld.wolfram.com/Epicycloid.html
http://mathworld.wolfram.com/WattsCurve.html

波粒二象性是脈衝函數做Laplace transform？

Fourier transform

fourier transform
https://i.imgur.com/LEzlfhQ.png

radial function與Fourier transform

e的純虛數次方會不斷繞圈。採用單位根的次方e^𝑖⋅2π/N。

複數　垂直座標　　轉換機制　　頻率座標　　轉換名稱　　時間複雜度
一一　一一一一一　一一一一一　一一一一一　一一一一一　一一一一一
數字　實部、虛部　長度、角度　幅長、幅角　極轉換　　　O(1)
函數　實部、虛部　複弦波　　　強度、相位　傅立葉轉換　O(NlogN)

一個數值，得到極座標表示法
一個數列，得到傅立葉轉換
一個矩陣，得到特徵分解

e^x              　輸入相加＝輸出相乘
fourier transform　輸入點積＝輸出卷積

傅立葉轉換也許可以視作座標系轉換。有些問題在垂直座標很難算，在頻率座標卻很好算。複數乘法變長度相乘、角度相加。數列卷積變數列乘法。

傅立葉轉換是積分變換，可以視作向量空間的座標系。

eigenvalue與Fourier transform

循環矩陣，特徵向量是傅立葉矩陣，特徵值是第一個橫條的傅立葉轉換。

1. 兩個循環矩陣相乘  = 總是可以用fourier matrix作對角化 = 對角線矩陣相乘
　 (還是循環矩陣)        (C = F D F⁻¹) (F⁻¹ = Fᵀ)　      (對應的eigenvalue相乘)

2. 兩串數列的循環卷積     = fft                         = 對應項相乘

3. 兩個多項式的循環乘法   = 多項式求值，以e^-itn取樣　　= 對應的點座標相乘

4. 兩串函數值的循環乘法   = 這是甚麼東西？

5. 兩串分解式的循環乘法   = 這是甚麼東西？
   (2n個根融合成n個根)

tridiagonal and Toeplitz matrix's eigenvalues:
a + 2 sqrt(bc) cos(k pi / (n+1))   for k = 1⋯n

eigenvectors of fourier matrix is gaussian function
eigenvalues of fourier matrix is +1 -1 +i -i
F^4 = I

傅立葉矩陣的特徵向量是高斯，特徵值是 {-1, +1, -i, +i}
https://en.wikipedia.org/wiki/Discrete_Fourier_transform#Eigenvalues_and_eigenvectors

循環矩陣的特徵向量是傅立葉，特徵值是傅立葉轉換結果
https://en.wikipedia.org/wiki/Circulant_matrix#Properties

共伴矩陣的特徵向量是 [1 x^1 x^2 ...] ，特徵值是遞迴方程式的根x。
det = 0 是原本的遞迴方程式。
https://en.wikipedia.org/wiki/Companion_matrix

chirp Z-transform

fast inverse CZT algorithm
Generalizing the inverse FFT off the unit circle
https://www.news.iastate.edu/news/2019/10/10/signalprocessing

https://en.wikipedia.org/wiki/Rader's_FFT_algorithm

函數輸入是兩個變數

float θ = random(-π, +π); float φ = random(-π, +π); float a′ = a + sin(φ) * cos(θ) * step; float b′ = b + sin(φ) * sin(θ) * step; float c′ = c + cos(φ) * step;

Radon transform / Hough transform

https://en.wikipedia.org/wiki/Radon_transform
https://en.wikipedia.org/wiki/File:R_theta_line.GIF
y = mx + b <---> (r,θ)

這跟計算幾何的點線對偶不一樣。