專著

已有熱心人士撰寫了排程問題的專著：

《Scheduling Algorithms》

《Scheduling: Theory, Algorithms, and Systems》

已有熱心人士彙整了排程演算法的參考文獻：

導讀

多種產品、多種設備。找到最佳製程，儘快完成所有產品。

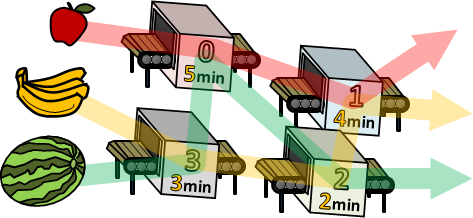
製程必須遵守規則。比方來說：

一、簡單起見，每種產品各一份，每種設備各一臺。

二、一份產品經由一臺設備加工，需要一段時間。

三、一種產品，擁有特殊的加工工序。一份產品，經過一連串指定設備，得到成品。

四、一種設備，同時間只能加工一份產品。一份產品，經過一臺設備，完成一道步驟。

不同產品可能需要相同設備。一個產品可能需要排隊等待某個設備。產品儘量不等待、設備儘量不停歇，以便儘快完成所有產品。

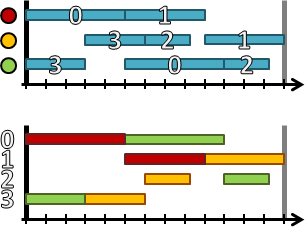
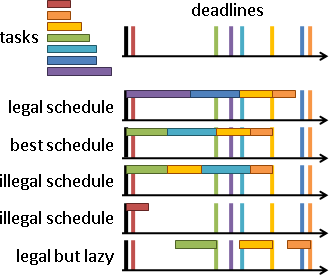
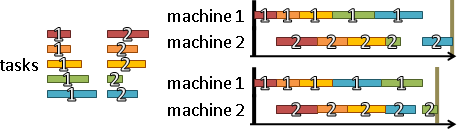
製程可以畫成圖表。最經典的圖表是「甘特圖Gantt Chart」：橫軸是時間，橫向區間是加工時間，縱軸是產品或設備。

Scheduling

上述詞彙都有專業術語：產品稱作「工作job」，設備稱作「機器machine」，加工稱作「操作operation」，製程稱作「排程scheduling」。

job        J₀ J₁ J₂ ...    工作
machine    M₀ M₁ M₂ ...    機器
operation  (j,m,t)         操作（工作編號、機器編號、時刻）
scheduling (j₀,m₀,t₀) ...  排程（操作的集合）

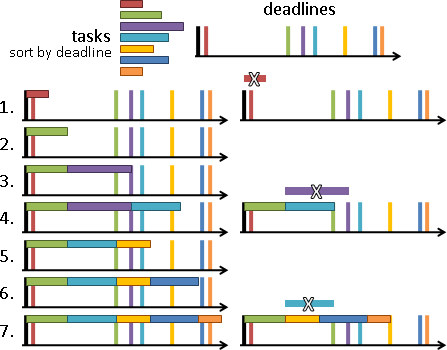
規則可以自由創作。給定特定規則，求得最佳排程。

機器順序的規則，可以自由創作。以下只列舉其中幾項：

open shop scheduling  每種工作在每種機器各做一次，機器順序隨便。
 job shop scheduling  每種工作有特定的機器順序。
flow shop scheduling  每種工作的機器順序都一模一樣。

操作的規則，可以自由創作。以下只列舉其中幾項：

operation sequence   Oᵢⱼ   機器順序（工作對機器）
processing time      pᵢⱼ   操作時間（工作對機器）
release time         rᵢ    工作發生時間（工作）
precedence relation  βᵢⱼ   工作優先順序（工作對工作）
transportation time  tᵢⱼₖ  工作換機時間（工作對兩機器）（額外工作時間）
changeover time      sᵢⱼₖ  機器換工時間（機器對兩工作）（額外機器時間）

最佳化目標，可以自由創作。以下只列舉其中幾項：

completion time      Cᵢ                    完工時間
due time             dᵢ                    完工期限
earliness            Eᵢ = max(0, dᵢ - Cᵢ)  提前時間
tardiness            Tᵢ = max(0, Cᵢ - dᵢ)  延誤時間

makespan             max Cᵢ                完工時間最大值
total flow time      sum Cᵢ                完工時間總和

排程問題，幾乎都是NP-hard問題，沒有快速的演算法。常見解法是整數規劃、啟發式演算法。

擁有特殊限制的排程問題，才有快速的演算法。常見解法是貪心法、動態規劃。

以下章節將介紹幾個特殊的排程問題，其解法都是貪心法。

UVa 452 690 863 1194 1380 12228

Minimize the Number of Tardy Jobs（1||∑Ui）

有一位苦命上班族，要馬上處理臨時指派的N份工作。經驗老到的他，馬上就精準的估計出每份工作各要花掉多少時間，可是每份工作都有不同的完工期限，這造成有些工作可能會來不及完成。他做事專心，要求品質，一次只處理一份工作，一份一份接著做；來不及完成的工作，乾脆放棄不做。

請找出一種排程，讓如期完成的工作最多（也就是讓逾期完成的工作最少），順便讓總工時越短越好。

合理排程之相鄰交換性質

一個合理排程，其中某兩個如期完成的工作A與B，A與B緊鄰完成，A早做B晚做，A期限晚B期限早（或期限相同），則A與B對調位置之後，仍是一個合理排程。分析如下：

A與B視作一體進行交換：排程裡的其他工作皆不受影響。
A放到B的位置：A的期限比B還晚，B都能如期完成了，所以A也能如期完成。
B放到A的位置：B提早做，更能如期完成。

一個合理排程，不斷地進行相鄰交換，終會形成「工作依照期限排序」的合理排程！反之亦然！小心，不相鄰則不可貿然交換。

因此，我們只需著眼於「工作依照期限排序」的合理排程。

UVa 10026 11389

演算法（Moore–Hodgson Algorithm）

所有工作依照期限排序，依序加入排程。一次加入一個工作，一旦發現逾期，立即從排程當中抽掉工時最長的工作。

已經加入N個工作，排程裡有M個工作。
排程裡的工作，是前N個工作的最佳解。也就是說：
α. 這M個工作，全部如期完成。
β. 前N個工作之中，如期完成的工作數量最多就是M。
γ. 前N個工作之中，這M個工作總工時最短。

以數學歸納法證明之。假設N成立，當第N+1個工作加入排程，有兩種情況。

一、沒有發生逾期：

這M個工作，本來就是如期完成、工作數量最多、總工時最短的最佳選擇。第N+1個工作加入之後，αβγ依然成立。

二、發生逾期，立即抽出工時最長的工作：

這M個工作，已經能如期完成。抽出工時最長的工作，補上工時稍短（或相等）的第N+1個工作，更能如期完成了。α成立。

這M個工作，總工時已經是最短了，還是無法添加第N+1個工作，不得已抽掉一個工作，工作數量已經盡量多了。β成立。

抽出工時最長的工作，總工時下降最多。γ成立。

const int N = 10; struct Job {int time, due;} job[N]; priority_queue<int> pq; bool cmp(Job& a, Job& b) { return a.due < b.due; } void Moore_Hodgson() { sort(job, job+N, cmp); int t = 0; for (int i=0; i<N; i++) { pq.push(job[i].time); t += job[i].time; if (t > job[i].due) t -= pq.top(), pq.pop(); } cout << "如期完成的工作數量，最多為" << pq.size(); cout << "逾期完成的工作數量，至少為" << N - pq.size(); } const int N = 10; struct Job {int time, due;} job[N]; bool operator<(Job& a, Job& b) { return a.due < b.due; } int heap[N], size = 0; void Moore_Hodgson() { sort(job, job+N); int t = 0; for (int i=0; i<N; i++) { heap[size++] = job[i].time; push_heap(heap, heap+size); t += job[i].time; if (t > job[i].due) { t -= heap[0]; pop_heap(heap, heap+size); size--; } } cout << "如期完成的工作數量，最多為" << size; cout << "逾期完成的工作數量，至少為" << N - size; }

UVa 10154 ICPC 3277 4850 8046

Minimize the Bottleneck Objective（1|prec|Fmax）

方才那位苦命上班族，又要馬上處理臨時指派的N份工作。本次任務更加艱辛刻苦、錯綜複雜。

一、每份工作都要確實完成。形成一個排列。

二、每份工作都有誤點賠償機制。完工時間越晚、賠償金額越大。形成N個遞增函數。

三、每份工作都有優先順序機制。有必須更早完成的工作、也有必須更晚完成的工作。形成一張有向無環圖。

請找出一種排程，讓賠償金額最高的工作，賠償金額越小越好。

演算法（Lawler's Algorithm）

排程從尾到頭，一次加入一個工作：賠償金額最小的工作。

const int N = 10; int time[N]; // 工時 int (*f[N])(int); // 遞增函數 int adj[N][N]; // 有向無環圖 bool schedule[N]; // 已經加入排程的工作 int outdeg[N]; // 必須更晚完成的工作數量 void Lawler() { // 總工時 int t = 0; for (int i=0; i<N; i++) t += time[i]; // 必須更晚完成的工作數量 for (int i=0; i<N; i++) { outdeg[i] = 0; for (int j=0; j<N; ++j) outdeg[i] += adj[i][j]; } // 排程，從尾到頭。 int fmax = 0, fmax_job = 0; for (int k=0; k<N; k++) { // 賠償金額最小的工作 int min = 1e9, min_job = 0; for (int j=0; j<N; ++j) if (!schedule[j] && !outdeg[j]) { int cost = f[j](t); if (cost < min) min = cost, min_job = j; } // 賠償金額最小的工作，加入排程。 schedule[min_job] = true; t -= time[min_job]; for (int i=0; i<N; ++i) if (!schedule[i]) outdeg[i] -= adj[i][min_job]; if (min > fmax) fmax = min, fmax_job = min_job; } cout << "賠償金額最高的工作是" << fmax_job; cout << "其賠償金額是" << fmax; }

Minimize the Makespan（F2||Cmax）

兩臺機器，N份工作，一臺機器一次只能處理一個工作。每份工作必須先經過初號機處理一段時間，再經過貳號機處理一段時間，才算處理完畢。

請找出一種排程，迅速完成所有工作。

演算法（Johnson's Algorithm）

1. 建立兩個空的List，叫做L1和L2。
2. 從N個工作、2N個工時當中，不斷挑出工時最短的工作。
   如果最短工時是初號機的工時，該工作加到L1前端。
   如果最短工時是貳號機的工時，該工作加到L2後端。
3. L1 L2，即是排程。

1. 建立兩個空的List，叫做L1和L2。
2. 對每一個工作，若初號機工時小於貳號機工時，該工作加到L1，反之則加到L2。
3. L1照初號機工時由小到大排序。
   L2照貳號機工時由大到小排序。
4. L1 L2，即是排程。

const int N = 10; int c1[N]; int c2[N]; bool cmp1(int i, int j) {return c1[i] < c1[j];} bool cmp2(int i, int j) {return c2[i] > c2[j];} void Johnson() { vector<int> l1, l2; for (int i=0; i<N; i++) if (c1[i] < c2[i]) l1.push_back(i); else l2.push_back(i); sort(l1.begin(), l1.end(), cmp1); sort(l2.begin(), l2.end(), cmp2); // vector<int> l = l1 + l2; vector<int> l(l1.size() + l2.size()); l.insert(l.end(), l1.begin(), l1.end()); l.insert(l.end(), l2.begin(), l2.end()); int t1 = 0, t2 = 0; for (int i=0; i<l.size(); i++) { t1 += c1[l[i]]; t2 = max(t1, t2) + c2[l[i]]; } cout << "總完成時間為" << t2; }

UVa 11269 11729