用途

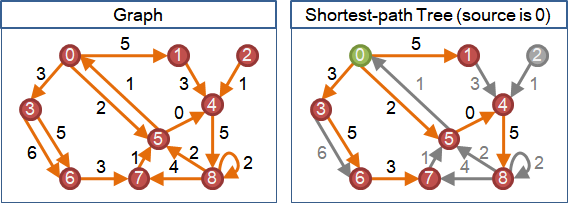
一張有向圖，選定一個起點，找出起點到圖上各點的最短路徑。即是找出其中一棵最短路徑樹。

限制是：圖上每一條邊的權重皆非負數。

想法

當最短路徑只有正邊和零邊，截去末端之後，仍是最短路徑，而且長度一定更短（也可能相同）。當有負邊，長度不會更短或相同，反而更長。

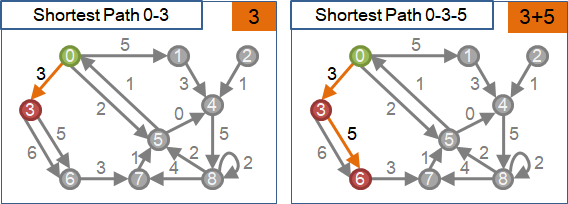
圖上有負邊，就必須使用label correcting algorithm。即使數值標記錯誤了，仍可修正。

圖上有負邊，則無法使用label setting algorithm。當下不在樹上、離根最近的點，以後不見得是最短路徑。

label correcting algorithm受負邊影響，不知道relaxation的正確順序，只好不斷修正每個點的最短路徑長度，直到正確為止。

label setting algorithm只有正邊、零邊，知道relaxation的正確順序，逐步設定每個點的最短路徑長度。

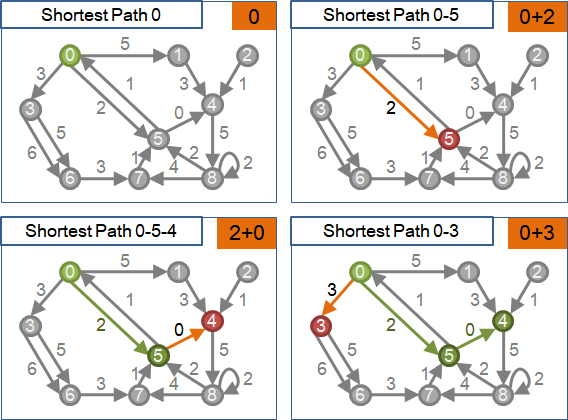
想法

當圖上每一條邊的權重皆非負數時，可以發現：每一條最短路徑，都是邊數更少、權重更小（也可能相同）的最短路徑的延伸。

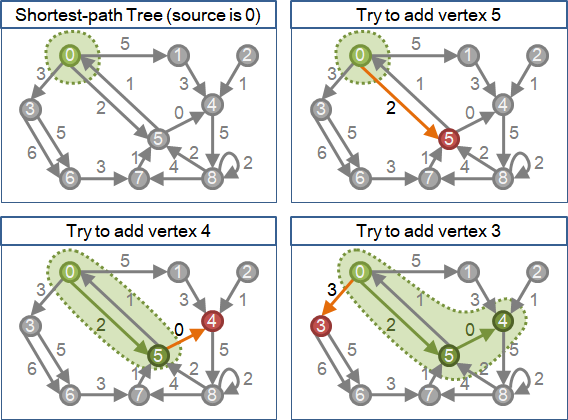
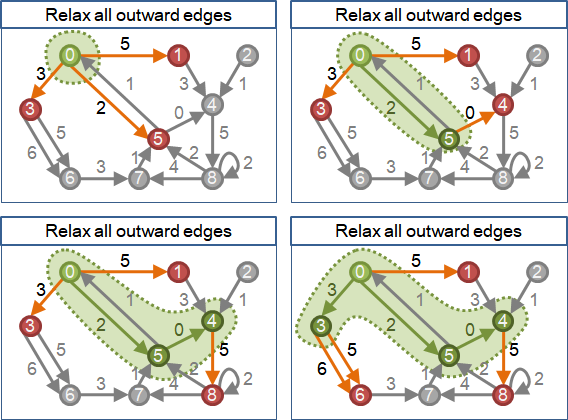
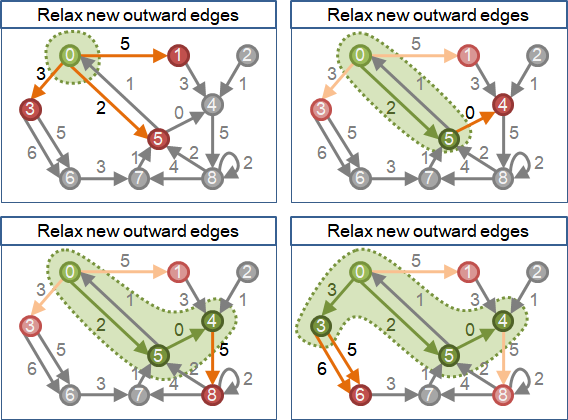
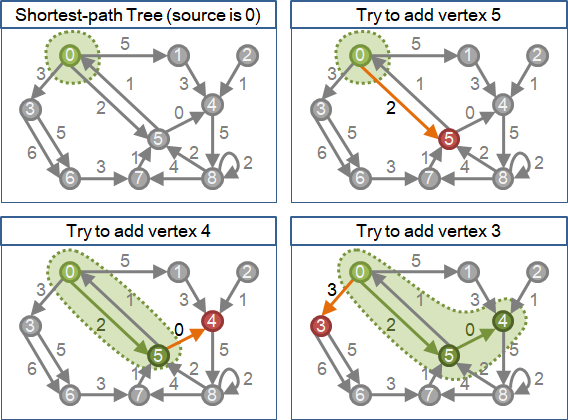
於是乎，建立最短路徑樹，可以從邊數最少、權重最小的最短路徑開始建立，然後逐步延伸拓展。換句話說，就是從距離起點最近的點和邊開始找起，然後逐步延伸拓展。先找到的點和邊，保證會是最短路徑樹上的點和邊。

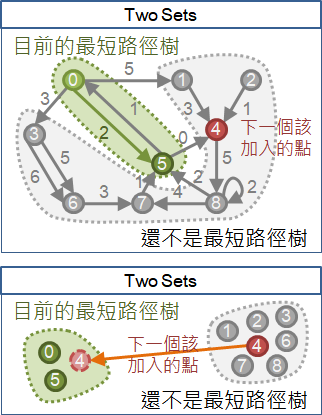
也可以想成是，從目前形成的最短路徑樹之外，屢次找一個離起點最近的點，（連帶著邊）加入到最短路徑樹之中，直到圖上所有點都被加入為止。

整個演算法的過程，可看作是兩個集合此消彼長。不在樹上、離根最近的點，移之。

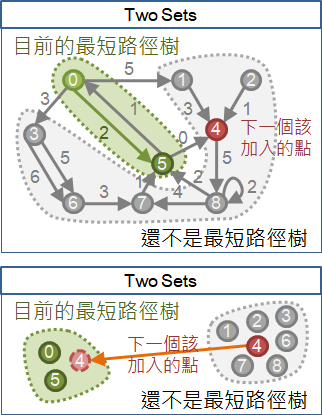
運用已知的最短路徑，求出其他的最短路徑。循序漸進、保證最佳，這是greedy method的概念。

整個演算法的過程，亦可看作是一種特殊的graph traversal，遍歷順序是優先拜訪離樹根最近的點和邊。

演算法

一、將起點加入到最短路徑樹。此時最短路徑樹只有起點。
二、重複下面這件事V-1次，將剩餘所有點加入到最短路徑樹。
　甲、尋找一個目前不在最短路徑樹上而且離起點最近的點b。
　乙、將b點加入到最短路徑樹。

建立表格記錄最短路徑長度，便容易求得不在樹上、離根最近的點。時間複雜度O(V³)。

令w[a][b]是a點到b點的距離（即是邊的權重）。
令d[a]是起點到a點的最短路徑長度，起點設為零，其他點都是空的。

一、將起點加入到最短路徑樹。此時最短路徑樹只有起點。
二、重複下面這件事V-1次，將剩餘所有點加入到最短路徑樹。
　甲、尋找一個目前不在最短路徑樹上而且離起點最近的點：
　　　以窮舉方式，
　　　找一個已在最短路徑樹上的點a，以及一個不在最短路徑樹上的點b，
　　　讓d[a]+w[a][b]最小。
　乙、將b點的最短路徑長度存入到d[b]之中。
　丙、將b點（連同邊ab）加入到最短路徑樹。

實作

int w[9][9]; // adjacency matrix int d[9]; // 記錄起點到圖上各個點的最短路徑長度 int parent[9]; // 記錄各個點在最短路徑樹上的父親是誰 bool visit[9]; // 記錄各個點是不是已在最短路徑樹之中 void label_setting(int source) { for (int i=0; i<9; i++) visit[i] = false; d[source] = 0; // 設定起點的最短路徑長度 parent[source] = source; // 設定起點是樹根（父親為自己） visit[source] = true; // 將起點加入到最短路徑樹 for (int k=0; k<9-1; k++) // 將剩餘所有點加入到最短路徑樹 { // 從既有的最短路徑樹，找出一條聯外而且是最短的邊 int a = -1, b = -1, min = 1e9; // 找一個已在最短路徑樹上的點 for (int i=0; i<9; i++) if (visit[i]) // 找一個不在最短路徑樹上的點 for (int j=0; j<9; j++) if (!visit[j]) if (d[i] + w[i][j] < min) { a = i; // 記錄這一條邊 b = j; min = d[i] + w[i][j]; } // 起點有連通的最短路徑都已找完 if (a == -1 || b == -1) break; // // 不連通即是最短路徑長度無限長 // if (min == 1e9) break; d[b] = min; // 儲存由起點到b點的最短路徑長度 parent[b] = a; // b點是由a點延伸過去的 visit[b] = true; // 把b點加入到最短路徑樹之中 } }

備註

label setting algorithm一共三個階段：圖論元件（點、邊、權重、陣列或串列）、貪心策略（最短路徑末端截去一段還是最短路徑，而且長度更短或相同）、紀錄路徑長度（陣列或堆積）。

Dijkstra只有發明貪心策略。那個時代的學者沒有探討圖資料結構、排序資料結構。也沒有探討時間複雜度。古時候沒有這些玩意。

使用不同的資料結構，得到不同的時間複雜度。以下假定圖資料結構是adjacency lists。以下列出各種不同的排序資料結構。

without ordered data structure
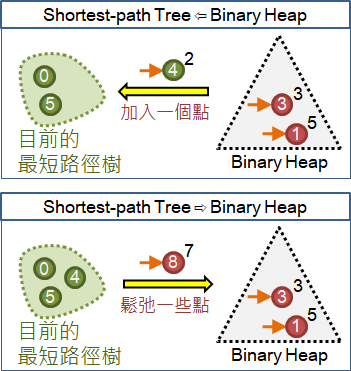
每回合掃描所有邊找到最小值，找出下一個點。
O(VE)

array (indexing by vertex)
抵達各點的最短路徑，儲存於各個元素。索引值是點編號。
這裡的array是集合資料結構：索引儲存。至今沒有正式名稱。
每回合掃描陣列找到最小值，找出下一個點。
O(V²)

binary heap
以push實作relaxation。
以pop找出下一個點。
O(V + ElogV)

Fibonacci heap
以decrease key實作relaxation。
以extract min找出下一個點
Fredman–Tarjan algorithm O(E + VlogV)

array (indexing by weight)
抵達各點的最短路徑，儲存於各個元素。索引值是最短路徑長度。
依序掃描陣列，找出下一個點。
Dial's algorithm O(V+E+L)，L是最長路徑長度。

van Emde Boas tree
同上。
O(V + EloglogL)

O(V²)演算法沒有正式名稱。早期教科書（例如AHU）明確告訴大家這是Dijkstra's algorithm的一種實作方式。後來有些教科書（例如CLRS）直接稱作Dijkstra's algorithm，導致大家搞錯，成為歷史共業。

接下來介紹的正是O(V²)演算法。

想法

找不在樹上、離根最近的點，先前的方式是：窮舉樹上a點及非樹上b點，找出最小的d[a]+w[a][b]。整個過程重覆窮舉許多邊。

表格改為儲存d[a]+w[a][b]，就不必重覆窮舉邊了。每當一個a點加入最短路徑樹，就將d[a]+w[a][b]存入d[b]。找不在樹上、離根最近的點，就直接窮舉d[]表格，找出最小的d[b]。

演算法

令w[a][b]是a點到b點的距離（即是邊的權重）。
令d[a]是起點到a點的最短路徑長度，起點設為零，其他點都設為無限大。

一、重複下面這件事V次，以將所有點加入到最短路徑樹。
　甲、尋找一個目前不在最短路徑樹上而且離起點最近的點：
　　　直接搜尋d[]陣列裡頭的數值，來判斷離起點最近的點。
　乙、將此點加入到最短路徑樹之中。
　丙、令剛剛加入的點為a點，
　　　以窮舉方式，找一個不在最短路徑樹上、且與a點相鄰的點b，
　　　把d[a]+w[a][b]存入到d[b]當中。
　　　因為要找最短路徑，所以儘可能記錄越小的d[a]+w[a][b]。
　　　（即是邊ab進行relaxation）

以relaxation的觀點來看，此演算法不斷以邊ab作為捷徑，讓起點到b點的路徑長度縮短為d[a]+w[a][b]。

時間複雜度

一、加入點、窮舉邊：每個點只加入一次，每條邊只窮舉一次，剛好等同於一次graph traversal的時間。

二、尋找下一個點：從大小為V的陣列當中尋找最小值，O(V)；總共尋找了V次，O(V²)。

圖的資料結構為adjacency matrix是O(V²)；圖的資料結構為adjacency lists是O(V+E+V²) = O(E+V²)，通常簡單寫成O(V²)。

在最短路徑問題當中，如果兩點之間有多條邊，只要取權重最小的邊來進行最短路徑演算法就行了。預先以O(V+E)時間掃描一次所有邊，保留權重最小的邊。也就是說，兩點之間只會剩下一條邊。也就是說，邊數至多C(V,2) = V(V-1)/2 = O(V²)條。也就是說，時間複雜度O(V+E+V²)可以改寫成O(V+V²+V²) = O(V²)。

實作

int w[9][9]; // adjacency matrix int d[9]; // 記錄起點到各個點的最短路徑長度 int parent[9]; // 記錄各個點在最短路徑樹上的父親是誰 bool visit[9]; // 記錄各個點是不是已在最短路徑樹之中 void label_setting_with_array(int source) { for (int i=0; i<9; i++) visit[i] = false; for (int i=0; i<9; i++) d[i] = 1e9; d[source] = 0; parent[source] = source; for (int k=0; k<9; k++) { int a = -1, b = -1, min = 1e9; for (int i=0; i<9; i++) if (!visit[i] && d[i] < min) { a = i; // 記錄這一條邊 min = d[i]; } if (a == -1) break; // 起點有連通的最短路徑都已找完 // if (min == 1e9) break; // 不連通即是最短路徑長度無限長 visit[a] = true; // 以邊ab進行relaxation for (b=0; b<9; b++) if (!visit[b] && d[a] + w[a][b] < d[b]) { d[b] = d[a] + w[a][b]; parent[b] = a; } } }

UVa 10801 10841 10278 10187 10039

演算法

d[a]+w[a][b]通通倒進binary heap。

找不在樹上、離根最近的點：從binary heap彈出邊（與點）。

relaxation：將邊（與點）塞入binary heap。

時間複雜度：維護binary heap

圖上每一條邊皆用於relaxation一次。binary heap前前後後一共塞入E條邊、頂多彈出E條邊。binary heap的大小是O(E)。

塞入一條邊需時O(logE)，塞入E條邊需時O(ElogE)。彈出亦然。維護binary heap需時O(ElogE)，通常簡單寫成O(ElogV)。

在最短路徑問題當中，如果兩點之間有多條邊，只要取權重最小的邊來進行最短路徑演算法就行了。預先以O(V+E)時間掃描一次所有邊，保留權重最小的邊。也就是說，兩點之間只會剩下一條邊。也就是說，邊數至多C(V,2) = V(V-1)/2 = O(V²)條。也就是說，時間複雜度O(ElogE)可以改寫成O(ElogV²) = O(2ElogV) = O(ElogV)。

時間複雜度

一次graph traversal的時間，加上維護binary heap的時間。

圖的資料結構為adjacency matrix是O(V² + ElogV)；圖的資料結構為adjacency lists是O(V+E + ElogV) = O(V + ElogV)。

這個演算法適用於邊數非常少的情況。

實作

// 要塞入binary heap的邊。 // ab是邊的兩端點，d是起點到b點可能的最短路徑長度。 struct Edge {int a, b, d;}; // C++標準函式庫的binary heap， // 是maximum heap，而不是minimum heap。 // 必須顛倒比大小的結果。 bool operator<(Edge e1, Edge e2) {return e1.d > e2.d;} int w[9][9]; // adjacency matrix int d[9]; int parent[9]; bool visit[9]; void label_setting_with_binary_heap(int source) { for (int i=0; i<9; i++) visit[i] = false; for (int i=0; i<9; i++) d[i] = 1e9; // C++標準函式庫的binary heap。 priority_queue<Edge> pq; int a = source; d[a] = 0; parent[a] = 0; visit[a] = true; for (int i=0; i<9-1; i++) { // 比大小的工作，交由binary heap處理。 for (int b=0; b<9; b++) if (!visit[b]) pq.push( (Edge){a, b, d[a] + w[a][b]} ); // 找出下一個要加入到最短路徑樹的邊（與點） Edge e = (Edge){-1, -1, 0}; while (!pq.empty()) { e = pq.top(); pq.pop(); if (!visit[e.b]) break; } // 起點有連通的最短路徑都已找完 if (e.a == -1 || e.b == -1) break; a = e.b; d[a] = e.d; parent[a] = e.a; visit[a] = true; } }

演算法

d[a]+w[a][b]，既存入d[]表格，也塞入binary heap。

找不在樹上、離根最近的點：不再窮舉d[]表格，改為從binary heap彈出。

relaxation：先檢查d[]表格，才塞入binary heap。

時間複雜度跟上個章節相同，但是效率更好。

實作

// 要塞入binary heap的點 // b是點，d是起點到b點可能的最短路徑長度。 // a可以提出來，不必放在Node裡。 struct Node {int b, d;}; bool operator<(Node n1, Node n2) {return n1.d > n2.d;} int w[9][9]; // adjacency matrix int d[9]; int parent[9]; bool visit[9]; void label_setting_with_array_and_binary_heap(int source) { for (int i=0; i<9; i++) visit[i] = false; for (int i=0; i<9; i++) d[i] = 1e9; // C++標準函式庫的binary heap priority_queue<Node> pq; d[source] = 0; parent[source] = source; pq.push((Node){source, d[source]}); for (int i=0; i<9; i++) { // 找出下一個要加入到最短路徑樹的點。 int a = -1; while (!pq.empty() && visit[a = pq.top().b]) pq.pop(); // 最後少pop一次，不過無妨。 if (a == -1) break; visit[a] = true; for (int b=0; b<9; b++) if (!visit[b] && d[a] + w[a][b] < d[b]) { d[b] = d[a] + w[a][b]; parent[b] = a; // 交由binary heap比較大小 pq.push( (Node){b, d[b]} ); } } }

UVa 10278 10740 10986

演算法

僅有理論上的價值，沒有實務上的價值。

建立V個元素的Fibonacci heap，用其decrease key函式來實作relaxation，用其extract min函式來找出下一個點，時間複雜度降為 O(V+E + VlogV) = O(E + VlogV)。

備註

Fibonacci heap是不切實際的資料結構。結構複雜，步驟冗長。儘管時間複雜度很低，但是執行時間很高。現實世界無人使用。

20世紀只有一本教科書（就是CLRS）講解Fibonacci heap，而且第四版已經刪除了。有些教師水平較差，無法分辨是非善惡，盲目崇拜名校聖經，導致他們至今仍在基礎演算法課程教授Fibonacci heap，糟蹋學生、秀優越感。大家多保重。

演算法

當權重不是整數，d[a]+w[a][b]通通拿去做bucket sort。

當權重都是整數，d[a]+w[a][b]通通拿去做counting sort。

時間複雜度：bucket sort

一、桶子們最多塞入E次、彈出E次。O(E)。

二、桶子們讀過一遍。O(L)。

當權重不是整數，時間複雜度O(ElogE + L)。

當權重都是整數，時間複雜度O(E+L)。

L是桶子數目，頂多是最長路徑長度（至多V-1條邊）、再加一。

時間複雜度

一次graph traversal的時間，加上bucket sort的時間。

當權重都是整數，圖的資料結構為adjacency matrix是O(V² + L)；圖的資料結構為adjacency lists是O(V+E+L)。

這個演算法適用於路徑普遍很短的情況。

實作：權重都是整數

int w[9][9]; // adjacency matrix int d[9]; int parent[9]; bool visit[9]; // 建立100個桶子。桶子採用queue。 // 桶子數量頂多是最長路徑長度（至多V-1條邊）、再加一。 list<pair<int,int>> bucket[100]; void dial(int source) { for (int i=0; i<9; i++) visit[i] = false; for (int i=0; i<9; i++) d[i] = 1e9; for (int i=0; i<100; i++) bucket[i].clear(); bucket[0].push_back({source, source}); // 由小到大掃描每個桶子 for (int i=0, n=0; i<9; i++) { // 找出下一個要加入到最短路徑樹的點 while (n < 100 && bucket[n].empty()) n++; if (n == 100) break; // 起點有連通的最短路徑都已找完 int a = bucket[n].front().first; parent[a] = bucket[n].front().second; d[a] = n; visit[a] = true; bucket[n].pop_front(); for (int b=0; b<9; b++) if (!visit[b] && w[a][b] != 1e9) { int l = d[a] + w[a][b]; bucket[l].push_back({b, a}); } } }

用途

限制是：圖上每一條邊的權重皆非負數、皆是整數。

演算法

scaling method，權重精度逐步上升。

權重視作二進位數字，從最高數量級開始，每回合添加一個位數，並且修正上回合與本回合的答案誤差。

重複以下步驟，每回合都求出當下的最短路徑：
一、每條邊權重翻倍：上回合的最短路徑長度隨著翻倍。
二、每條邊權重加零或加一：修正最短路徑長度的誤差。
　甲、調整權重：扣除上回合的最短路徑長度的兩倍。《Johnson's algorithm》
　乙、調整後的權重，求最短路徑長度。《Dial's algorithm》
　　　（調整後的權重皆非負數，最短路徑長度至多是E。）
　丙、還原權重：補足上回合的最短路徑長度的兩倍。
　　　得到本回合的最短路徑長度。

權重加倍，不影響最短路徑位置。最短路徑長度隨著翻倍。

權重加零或加一，整張圖頂多增加E條邊、權重為1。最差情況是全部聚集於同一條最短路徑，最短路徑長度頂多增加E。

調整權重之後，最短路徑長度頂多是E，只需要E+1個桶子。

時間複雜度

總共O(logW)回合。W是最大的邊權重。

舉例來說，unsigned int總共32個位元，總共32回合。int非負數部分總共31個位元，總共31回合。

圖的資料結構為adjacency matrix是((V² + E)logW)；圖的資料結構為adjacency lists是O((V+E)logW)。