T-join
T-join
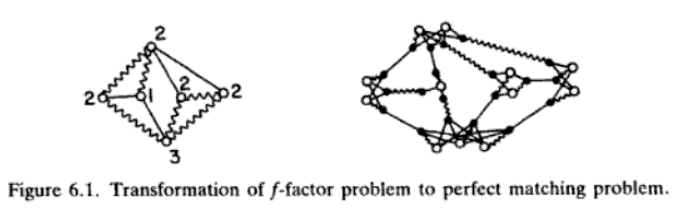
在一張圖上選出偶數個點(通常標作T集合,也就是T-join的T;因為是代表集合,所以T要大寫),然後再選出許多條邊,讓選中的點都是連著奇數條選中的邊,讓沒選中的點都是連著偶數條選中的邊,這些邊就叫做一個T-join。
這個定義是參考Euler path設計出來的。各位如果熟悉Euler path的起點和終點是「奇點」,中繼點是「偶點」,那麼就能了解這個定義的前因後果了!在圖上選出的偶數個點,正是Euler path的起點和終點。額外添上幾個環,便是T-join了。
minimum weight T-join
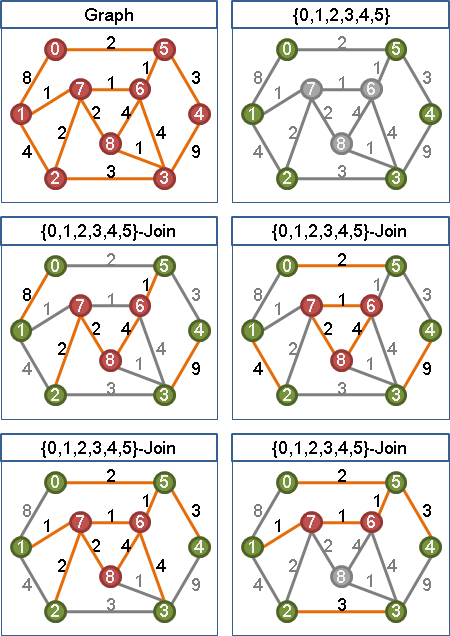
一張無向圖上,邊的權重總和最小的T-join,可能有許多種。
minimum weight T-join可以看作是matching的「匹配邊」改成了「匹配路徑」。匹配路徑數量是T的一半。每一條匹配路徑,顯然必須是最短邊互斥路徑。
minimum weight T-join是「最短邊互斥路徑」與「最小權匹配」兩者結合,同時具有兩者性質。
一、最短邊互斥路徑性質:一個minimum weight T-join由許多條匹配路徑組成,數量是T的一半。每一條匹配路徑,都是最短邊互斥路徑。
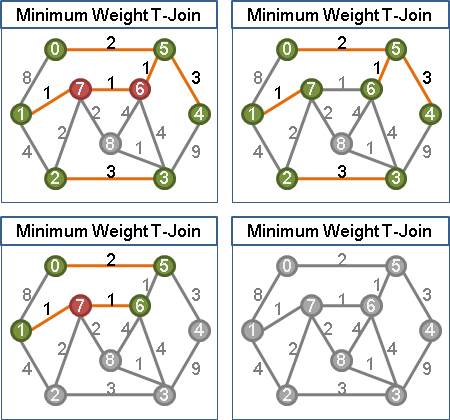
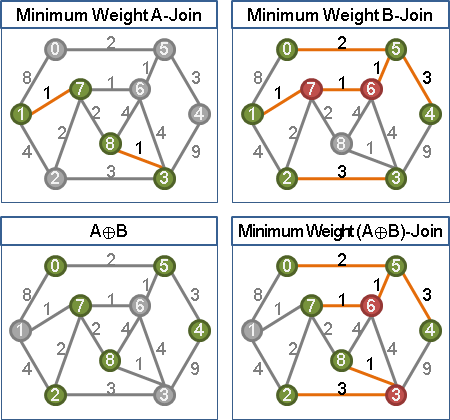
二、最小權匹配性質:兩種minimum weight T-join的互斥聯集,仍是一種minimum weight T-join。詳細的數學式子是:
minimum weight (A⊕B)-join = minimum weight A-join ⊕ minimum weight B-join。
⊕是對稱差集,也就是XOR。這個數學式子是XOR分配律。
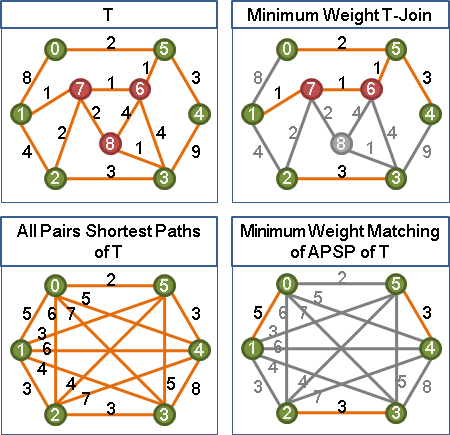
正權重圖的minimum weight T-join演算法
一、替T求出所有兩點之間的最短路徑長度。 二、替T找一個最小權匹配。此即minimum weight T-join。
第一步根據最短邊互斥路徑性質,第二步根據最小權匹配性質。
正權重圖的情況下,最短邊互斥路徑等同最短路徑。
正權重圖的情況下,所有匹配路徑,絕不會有邊重疊。兩條匹配路徑,一旦有邊重疊,只要去掉重疊的邊,仍然形成兩條匹配路徑,而且勢必形成權重更小的T-join。
負權重圖的minimum weight T-join演算法【尚待確認】
只適用於沒有負環的情況。有負環成為NP-complete問題。
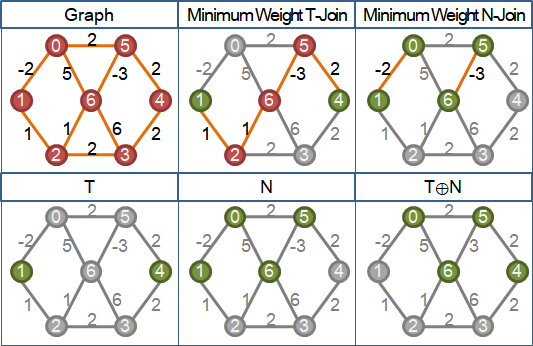
負權重圖改為正權重圖,然後利用正權重圖的minimum weight T-join反向推導負權重圖的minimum weight T-join。
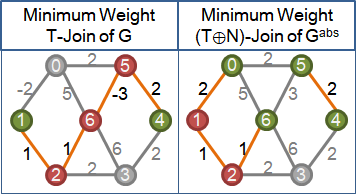
一、圖上所有負邊,恰好構成minimum N-join。 N是所有負邊的所有端點,而且重複次數是奇數。 N是連著奇數條負邊的點。 二、原圖所有負邊變號,得到新圖。 求出新圖的minimum weight (T⊕N)-join。 三、新圖的minimum weight (T⊕N)-join, 原圖的minimum N-join, 兩者的互斥聯集,即是原圖的minimum weight T-join。
我目前讀過的文獻,正確性證明千篇一律存在漏洞。
證明方式:原圖的minimum T-join,嘗試放到新圖上面。
w(T̅) = w(T̅-N̅) + w(T̅∩N̅)
= w(T̅-N̅) - w(N̅-T̅) + w(N̅-T̅) + w(T̅∩N̅)
= |w|(T̅-N̅) + |w|(N̅-T̅) + w(N̅-T̅) + w(T̅∩N̅)
^^^^^^^^^^^^^^^^^^^ ^^^^^^^^^^^^^^^
= |w|(T̅⊕N̅) + w(N̅)
^^^^^^^^ ^^^^
= |w|(T⊕N) + w(N̅)
T:取偶數個點。
T̅:minimum weight T-join的所有邊。
N:所有負邊的所有端點,而且重複次數是奇數。
N̅:所有負邊。顯然構成了minimum weight N-join。
T⊕N:T和N的互斥聯集。
T⊕N:minimum weight (T⊕N)-join的所有邊。
w():每條邊的權重總和。
|w|():每條邊的權重,先取絕對值(所有負邊變號)再總和。
w(T̅):minimum weight T-join的權重。
w(N̅):minimum weight N-join的權重。所有負邊的權重總和。
當|w|(T⊕N)達到最小值,而w(N̅)是常數,則w(T̅)也達到最小值。
大家只證明到這一步。大家並未證明原圖的minimum weight (T⊕N)-join和新圖的minimum weight (T⊕N)-join如何對應。
我認為兩者根本無法對應。一般來說,圖上某些邊,權重增減、甚至變號,minimum weight T-join都會大幅改變。
我認為上述演算法是古人瞎掰的。負權重圖的多項式時間演算法,也許根本不存在。
備忘
一、正權重圖,最短路徑截取一段路徑,仍是最短路徑。minimum weight T-join拿掉一些邊(T隨之變成T'),仍是minimum weight T'-join。
二、minimum weight T-join內部取一些正邊轉負邊【這部分是錯的】、外部取一些負邊轉正邊。原圖也轉換這些邊,成為新圖。它仍是新圖的minimum weight T-join。
應用
無向圖的最短邊互斥路徑:以起點與終點作為T。(恰是最短點互斥路徑) 無向圖的中國郵差問題:以所有奇點作為T。